【LuoguP5004】 专心OI - 跳房子

首先这是一道计数类DP，那我们得先推式子，经过瞎掰乱凑，经过认真分析，我们可以得到这样的方程

F(N)=F(0)+F(1)+....+F(N-M-1)

所有F初值为1，F(1)=2

ANS=F(N+M);

那显然我们有这样的代码：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 const int M=1e9+;
 using namespace std;
 inline int read(){
     char chr=getchar();    int f=,ans=;
     while(!isdigit(chr)) {if(chr=='-') f=-;chr=getchar();}
     while(isdigit(chr))  {ans=(ans<<)+(ans<<);ans+=chr-'';chr=getchar();}
     return ans*f;
 }
 void write(int x){
     if(x<) putchar('-'),x=-x;
     if(x>) write(x/);
     putchar(x%+'');
 }int n,m,f[];
 int main(){
     n=read(),m=read();
     f[]=;f[]=;
     for(int i=;i<=n+m;i++){
         f[i]=;
         for(int j=;j<=i-m-;j++)
             if(f[i]+f[j]>M) f[i]=f[i]+f[j]-M;
             else f[i]=f[i]+f[j];//卡一波时间
     }cout<<f[n+m];
     return ;
 }

显然这是O（n^2）的算法，然而面对N=1e18，这个算法可以去优化见鬼了，这样子由于语句比较简单，勉强可以过十万的数据大概30分

考虑优化：

我们先看一下上面的式子，尝试对这个式子变形...好吧，其实就是迭代，然后用鸽笼原理一通乱搞：

F(N)=F(N-1)+F(N-M-1)

ANS=F(N)

好了我们把这个东西优化得到了O(N)的算法：

期望得分：50pts

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 const int M=1e9+;
 using namespace std;
 inline int read(){
     char chr=getchar();    int f=,ans=;
     while(!isdigit(chr)) {if(chr=='-') f=-;chr=getchar();}
     while(isdigit(chr))  {ans=(ans<<)+(ans<<);ans+=chr-'';chr=getchar();}
     return ans*f;
 }
 void write(int x){
     if(x<) putchar('-'),x=-x;
     if(x>) write(x/);
     putchar(x%+'');
 }int n,m,f[];
 int main(){
     n=read(),m=read();
     f[]=;f[]=;
     for(int i=;i<=n;i++)
         f[i]=(f[i-]+f[max(i-m-,)])%M;
     cout<<f[n];
     return ;
 }

考虑继续优化

某个大佬说过1e18的数据考虑logn的算法，比如快速幂。

这既然是DP，那自然往矩阵乘法考虑。

　　考虑构造矩阵：m这么小，而且递推式中出现的常量只有m，显然矩阵的大小要往m*m考虑

　　m=1的时候斐波那契，显然不用我推了

　　看一下其他情况：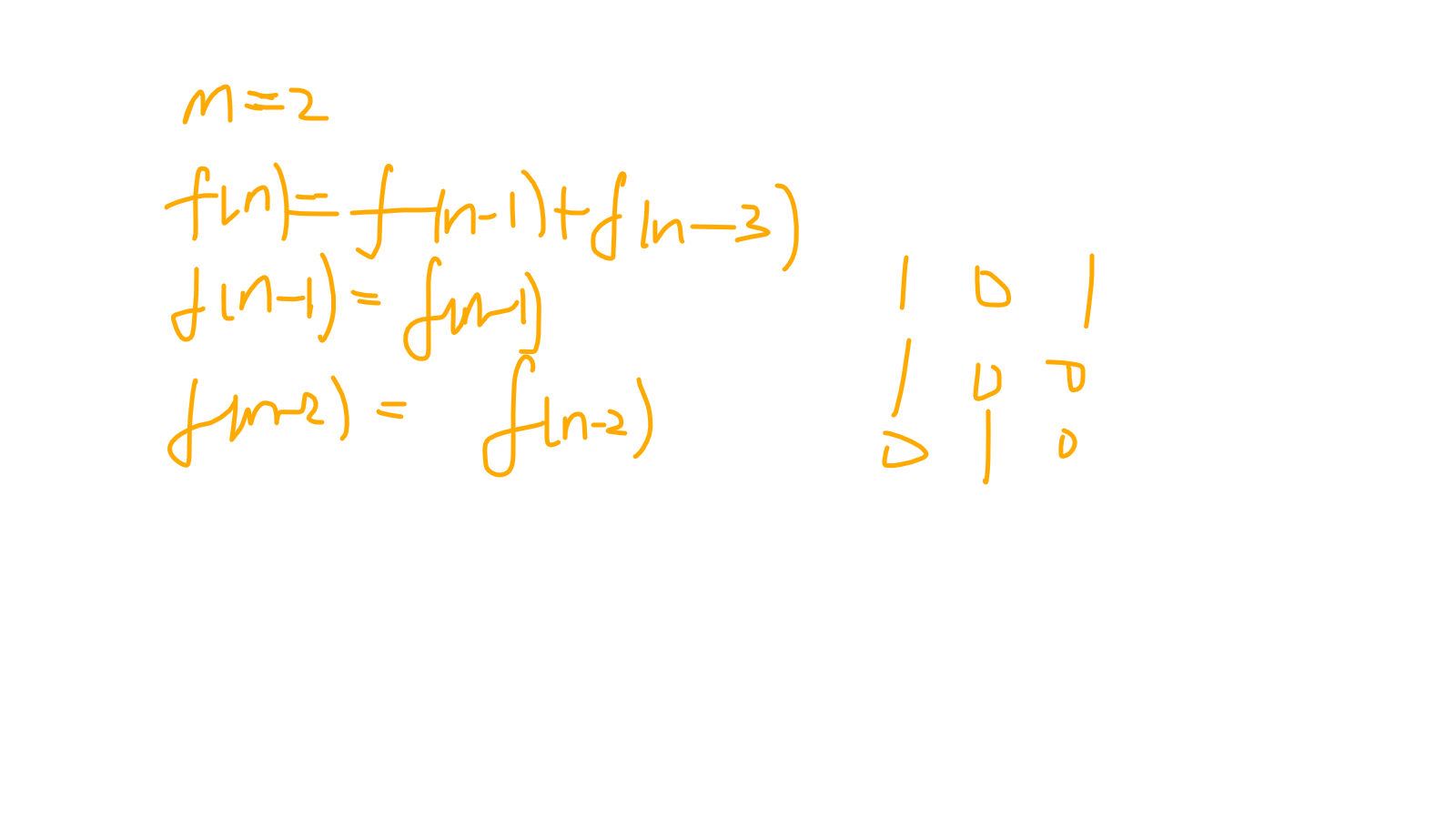

　　

得到通式（写了的是1，其他是0）：

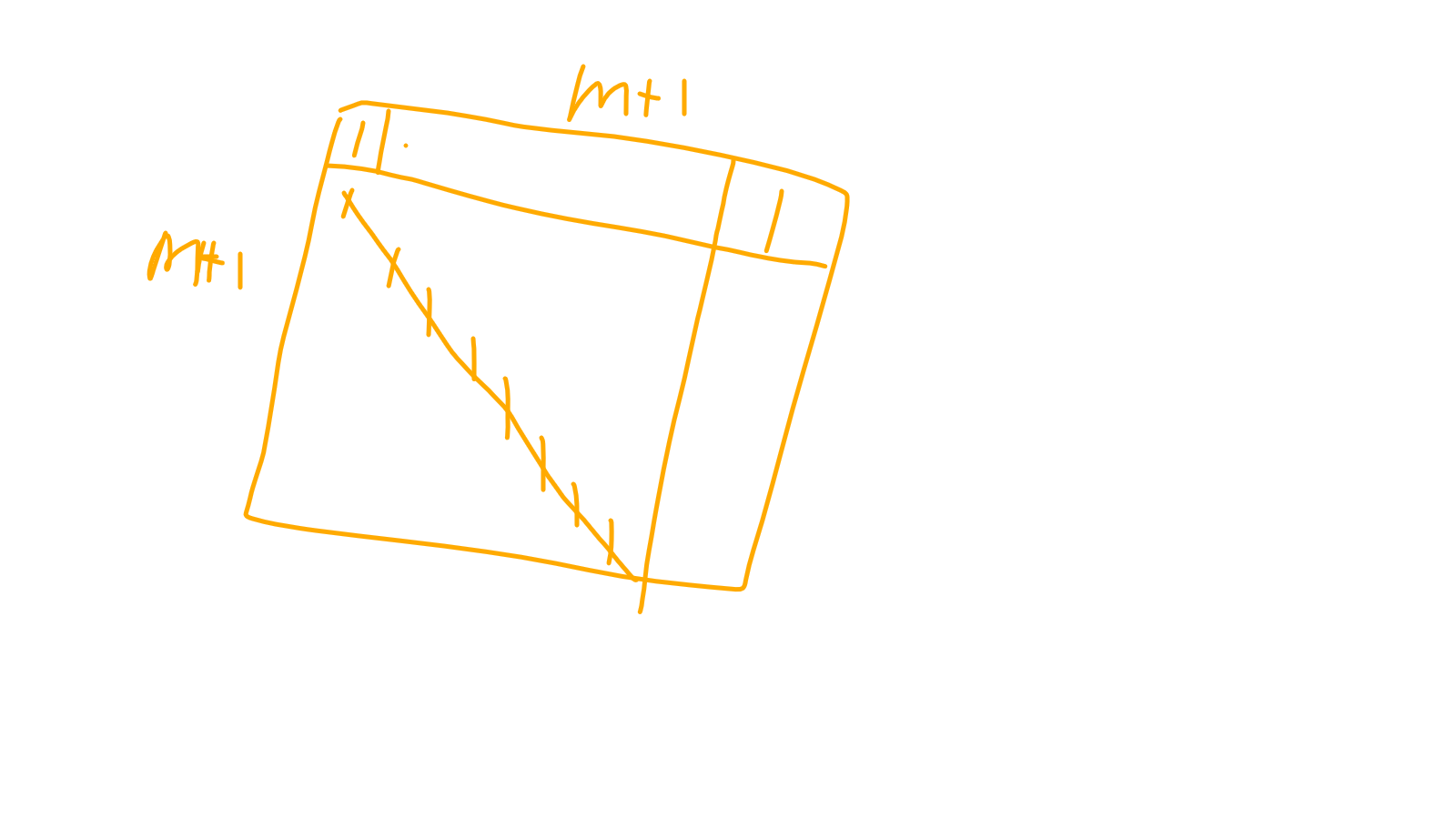
然后会矩阵加速的同学都知道该怎么做了吧...

 // luogu-judger-enable-o2
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define int long long
 const int M=1e9+;
 using namespace std;
 inline int read(){
     char chr=getchar();    int f=,ans=;
     while(!isdigit(chr)) {if(chr=='-') f=-;chr=getchar();}
     while(isdigit(chr))  {ans=(ans<<)+(ans<<);ans+=chr-'';chr=getchar();}
     return ans*f;
 }
 void write(int x){
     if(x<) putchar('-'),x=-x;
     if(x>) write(x/);
     putchar(x%+'');
 }int n,m;
 struct P{int a[][];P(){memset(a,,sizeof(a));}}A,B;
 P operator *(const P &x,const P &y){
     P ans;
     for(int i=;i<m;i++)
         for(int k=;k<m;k++)
             for(int j=;j<m;j++)
                 ans.a[i][j]=(ans.a[i][j]+x.a[i][k]*y.a[k][j])%M;
     return ans;
 }
 void KSM(int n){
     while(n){
         if(n&) B=B*A;
         n>>=;A=A*A;
     }
 }
 inline void init(){
     n=read(),m=read();--n,++m;
     A.a[m-][m-]=A.a[][m-]=;
     for(int i=;i<m-;i++)    A.a[i+][i]=;//初始矩阵
     for(int i=;i<m;i++)B.a[][i]=i+;
 }
 signed main(){
     init();KSM(n);
     write(B.a[][]);
     return ;
 }