FP增长算法

Apriori原理:如果某个项集是频繁的，那么它的所有子集都是频繁的。

Apriori算法：

1 输入支持度阈值t和数据集
2 生成含有K个元素的项集的候选集（K初始为1）
3 对候选集每个项集，判断是否为数据集中某条记录的子集
4        如果是：增加候选集的计数
5 保留频繁集（计数>t）
6 根据频繁集生成含有K+1个元素的项集候选集
7 循环2-5，直至候选集为空

Apriori算法是有缺点的

缺点是：1.需要多次扫描数据库 2.产生大量的候选频繁集 3.时间和空间复杂度高。

从算法第3步可以看出，候选频繁项集不一定是原始数据集中某一项的子集，即：x为频繁项，y为频繁项，{x，y}可以组成一个候选频繁项集，但是原始数据集中不一定存在{x，y}的组合。这使得Apriori算法有大量时间浪费在无效的集合上。

FP树增长算法是一种挖掘频繁项集的算法。Apriori算法虽然简单易实现，效果也不错，但是需要频繁地扫描数据集，IO费用很大。FP树增长算法有效地解决了这一问题，其通过两次扫描数据集构建FP树，然后通过FP树挖掘频繁项集。

背景知识

1.什么是项和项集?

比如我们在购物的时候，购物车内的每一件商品成为一项，若干个项的集合成为项集。例如{啤酒，尿布}成为一个二元项集。

2.什么是支持度?

支持度是在所有的项集中{X,Y}出现的可能性。

例如：购买商品的数据是(表示4条购物信息)：

①{啤酒，尿布,娃哈哈}

②{啤酒，方便面}

③{尿布,奶粉}

④{啤酒，尿布,洗发水}

在这组数据中,{啤酒，尿布}出现的可能性就是这里面数据的概率。{啤酒，尿布}的支持度是2/4=50%.

{尿布,奶粉}的支持度是1/4=25%

3.什么是频繁项集?

我们首先设置一个最小阈值A，支持度大于A的项集就是频繁项集，小于A的项集被剔除。

比如 我们设置阈值为30%,在上面的例子中{啤酒，尿布}就是频繁项集，{尿布,奶粉}就要被剔除。

问题：如何求出频繁项集?

首先构造FP树

然后通过FP树可以求出频繁项集

FP算法

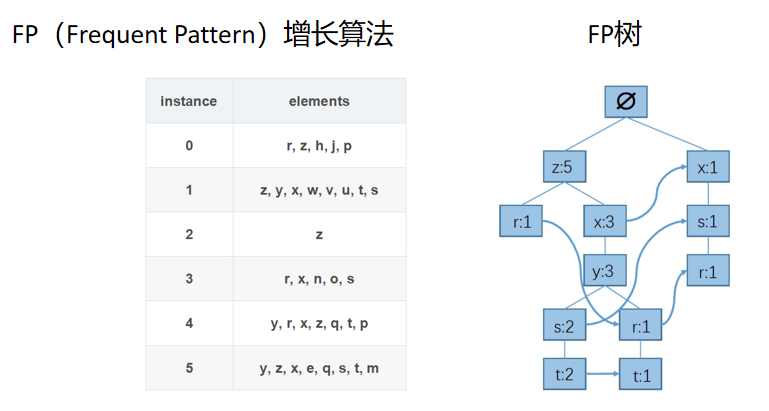
FP增长算法需要根据数据集生成FP树，步骤如下：

步骤一：统计每个元素出现次数，保留频繁元素（假设次数>3），按照元素出 现次数降序排序。

其中h,j,p,w,v,u,n,o,q,p,e,m的次数是小于等于3的.因此把它们去掉，然后把其他的字母按照次数从大到小排列。

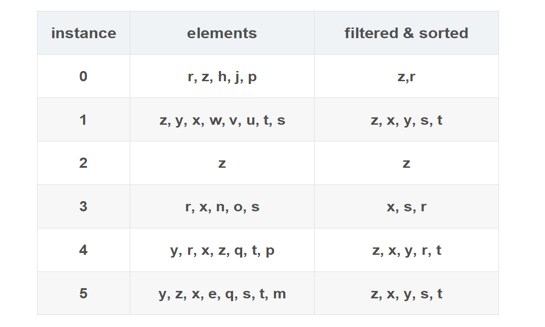
步骤二：构建FP树

通过上面的序列按照每一行进入树根初始化树叶。如果没有相同的字母就重新创建叶子节点，每个叶子节点有字母其次数。

如图所示

先插入(z,r)，再插入(z,x,y,s,t),再插入(z)，如图

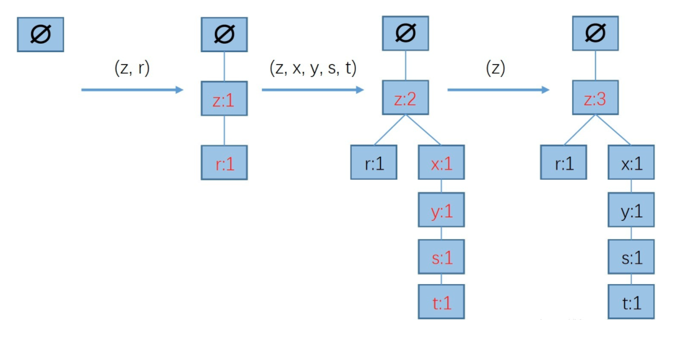
最后插完的结果是：

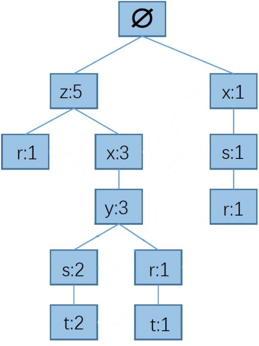
步骤三：FP树中找到元素的前缀路径

以r为例，r的前缀路径为：以根结点为起点，结点r为终点的所有路径。

先找到FP树中所有“r”结点，然后从每一个“r”结点向根结点方向查找，找到的所有路径就是“r”的前缀路径

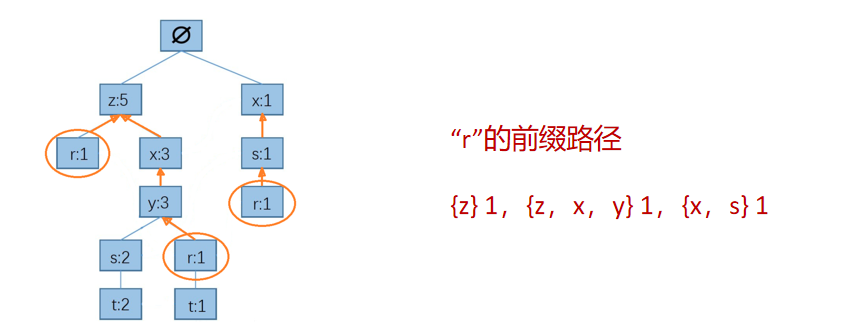
然而，找到所有“r”结点，需要遍历整棵FP树，这使得算法的时间复杂度会很高。

为了方便查找，可以用链表来加快寻找的前缀路径。

将FP树中所有相同的结点用链表连接，可以将查找结点的时间复杂度从O(n)降到常数级。

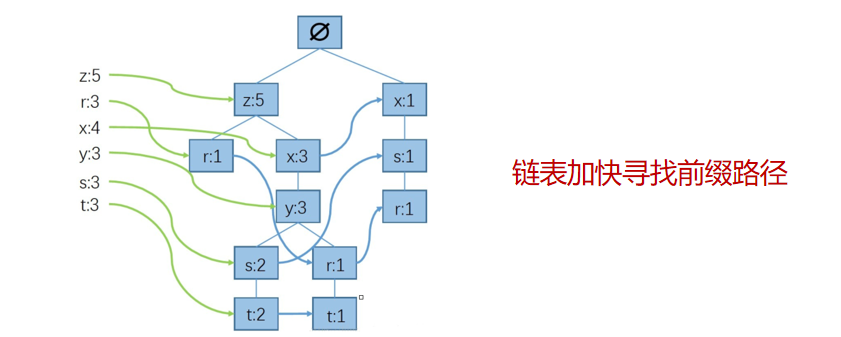
通过上面的操作就得到了如下所示的信息。

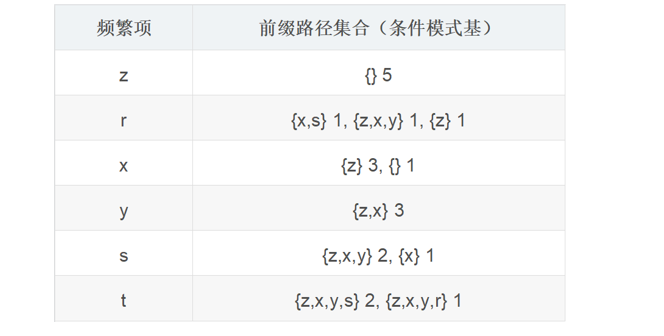
步骤四:根据前缀路径构造条件FP树

t的条件FP树如下：

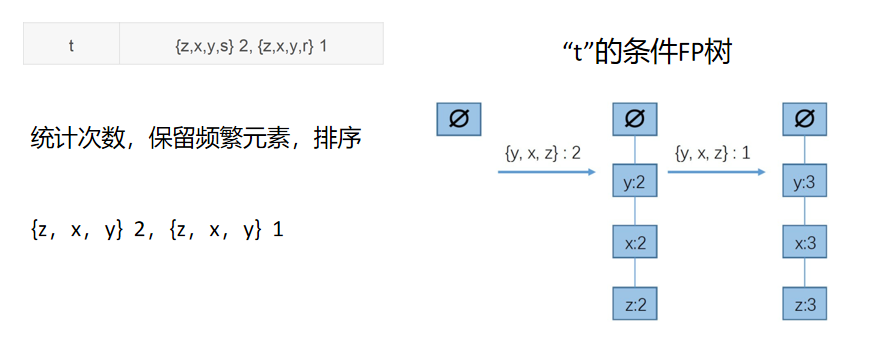
t前缀路径中的频繁元素包括{z：3，x：3，y：3}，这个数字表示对应的元素在原始数据集中和t一起出现的次数，如{z，t}出现3次，{x，t}出现3次，{y，t}出现3次。显然，这些项集都是频繁项集。

很容易发现，t的前缀路径也是一个数据集，生成t条件FP树的过程，跟前面生成FP树的过程相同，我们也可以在t的条件FP树基础上构造x的条件FP树，对应的就是{t，x}的条件FP树。

显然，这是个递归的过程。

步骤5:递归构造下一层条件FP树，直至条件FP树为空.

总结：

1、频繁集不是从FP树产生，而是通过每一层递归获得的频繁元素组合产生。FP树的作用是寻找前缀路径。
   相比于Apriori算法，FP树的作用相当于是把遍历数据集的结果用树的结构保存下来，而避免了重复扫描数据集。
2、FP树只需要扫描两次数据集，第一次统计各个元素出现次数，第二次根据过滤排序后的数据集生成FP树。后续的过程都在FP树上进行。
3、{x，t}的条件FP树和{t，x}的条件FP树是否相同？ 算法是否重复计算了这两个条件FP树？
   这个问题涉及到FP增长算法的一个根本问题，为什么要使用前缀路径？
   找到前缀路径后，需要对前缀路径集合进行过滤和排序，获得下一层递归的数据集。
   那么不使用前缀路径，而使用完整路径显然也可以达到目的。
   前缀路径有个非常重要的优点。
   构造FP树之前由于对元素进行了排序，如果x出现在t的前缀路径中，那么t不可能再出现在x的前缀路径中，所以使用前缀路径避免了相同集合的重复计算！
   另外，前缀路径的查找非常方便，一个结点向上查找，获得的前缀路径是固定的，如果使用完整路径，结点向下查找可能会出现分叉，处理起来会变得非常复杂。