工作组规划器(Project)
《Project2016 企业项目管理实践》张会斌 董方好 编著
好像前面每分配一次任务,都要打开一个对话框,有木有简单粗暴点的法子啊?
必须有啊!
视图里有一种【工作组规划器】,想要粗暴找他就对了。

整个界面看着也辣么简单粗暴哈,左边资源名,右边任务,有木有分配资源上下分开。

然后呢?然后就用肉眼看啊,很明显某吃货甲超负荷了,而某吃货乙却没事干。
再然后呢?再然后鼠标拖放呗,把超负荷的某吃货甲所负担的其中一个任务选取了,拖给某吃货乙,再放开鼠标。
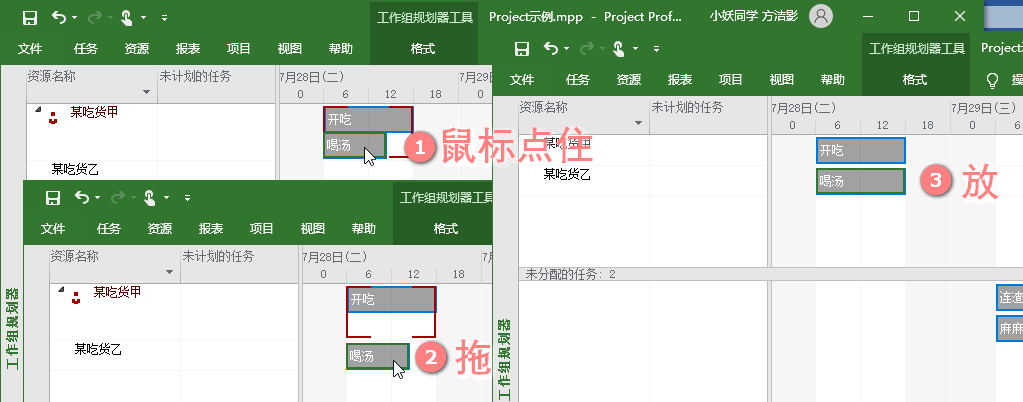
再再然后呢?再再然后就没有了。
是啊,大家没有红脸了,那还不皆大欢喜啊。
工作组规划器(Project)的更多相关文章
- Project简介
Microsoft Project (Project)是一个国际上享有盛誉的通用的项目管理工具软件,凝集了许多成熟的项目管理现代理论和方法,可以帮助项目管理者实现时间.资源.成本的计划.控制,协助项目 ...
- 与你一起学习MS Project——基础篇:Project基础应用
为了更清晰容易地熟悉掌握Project的基础应用,我们在基础篇中一起来学习掌握在Project中如何做进度计划.资源计划.成本计划以及跟踪项目的执行情况并生成所需的项目报表. 一.进度计划 这里,首先 ...
- 【项目管理工具】—— Microsoft Office Project 介绍
Project是由微软开发的项目管理软件.设计的目的在于协助项目经理发展计划,为任务分配资源.跟踪计划.管理预算和分析工作量. 对于我们之前的项目来说,之前的整体计划和WBS任务分解都是通过Excel ...
- 资源分配情况(Project)
<Project2016 企业项目管理实践>张会斌 董方好 编著 资源的分配情况,无非就是未分配.已分配和过度分配三种,这些都可以通过各种视图查看,比如[资源]>[工作组规划器]视图 ...
- 如何用MoveIt快速搭建机器人运动规划平台?
MoveIt = RobotGo,翻译成中文就是“机器人,走你!”所以,MoveIt的主要就是一款致力于让机器人能够自主运动及其相关技术的软件,它的所有模块都是围绕着运动规划的实现而设计的. 两个月前 ...
- move_base的 局部路径规划代码研究
base_local_planner teb_local_planner parameter code g2o base_local_planner ROS wiki Given a plan to ...
- 跟我一起读postgresql源码(四)——Planer(查询规划模块)(上)
时间一晃周末就过完了,时间过得太快,不由得让人倍加珍惜.时间真是不够用哈~ 好的不废话,这次我们开始看查询规划模块的源码吧. 查询规划部分的在整个查询处理模块应该是在一个非常重要的地位上,这一步直接决 ...
- EXPLAIN - 显示语句执行规划
SYNOPSIS EXPLAIN [ ANALYZE ] [ VERBOSE ] statement DESCRIPTION 描述 这条命令显示PostgreSQL规划器为所提供的语句生成的执行规划. ...
- ros局部路径规划-DWA学习
ROS的路径规划器分为全局路径和局部路径规划,其中局部路径规划器使用的最广的为dwa,个人理解为: 首先全局路径规划会生成一条大致的全局路径,局部路径规划器会把全局路径给分段,然后根据分段的全局路径的 ...
随机推荐
- [tc13008]Egalitarianism2
考虑对于$n-1$个数$a_{i}$,函数$f(x)=\frac{\sum_{i=1}^{n-1}(x-a_{i})^{2}}{n-1}$的最小值恰在$x=\frac{\sum_{i=1}^{n-1} ...
- Spring Cloud Gateway过滤器精确控制异常返回(实战,完全定制返回body)
欢迎访问我的GitHub 这里分类和汇总了欣宸的全部原创(含配套源码):https://github.com/zq2599/blog_demos 本篇概览 Spring Cloud Gateway应用 ...
- IDEA 2021.2.3 安装与破解教程
首先说明,大部分情况下,花10块钱都可以在淘宝找人直接帮你完美解决这个资源问题 所以千万不要相信一些所谓的百度结果,一般都是花费了时间却最后无法解决破解的问题 我相信任何一个想要学习软件开发的人一定要 ...
- CF1592F2 Alice and Recoloring 2
目前在看贪心/构造/DP 杂题选做,发现一道非常不错的结论题,具有启发意义. 先说明如下结论 结论一:如何怎么样都不会使用二和三操作 证明: 二三操作显然可以通过两次一操作达到,而其操作费用大于两次一 ...
- 洛谷 P6570 - [NOI Online #3 提高组] 优秀子序列(集合幂级数+多项式)
洛谷题面传送门 首先 \(3^n\) 的做法就不多说了,相信对于会状压 dp+会枚举子集的同学来说不算困难(暴论),因此这篇博客将着重讲解 \(2^nn^2\) 的做法. 首先如果我们把每个 \(a_ ...
- Atcoder Grand Contest 001E - BBQ Hard(组合意义转化,思维题)
Atcoder 题面传送门 & 洛谷题面传送门 Yet another 思维题-- 注意到此题 \(n\) 数据范围很大,但是 \(a_i,b_i\) 数据范围很小,这能给我们什么启发呢? 观 ...
- [转载]CSP-J/S 第一轮知识点选讲
CSP-J/S 第一轮知识点选讲 转载自这里 感谢原博主的大力整理! 信息学史及基本知识 一.信息学及计算机史 计算机的顶级奖项:图灵奖.冯·诺依曼奖 图灵奖:由ACM(美国计算机协会)设立于1966 ...
- BaiduPCS-Go----百度云下载工具
1.网页登录百度网盘:https://pan.baidu.com/2.百度输入法生成:http://pcs.baidu.com/rest/2.0/pcs/file?app_id=265486& ...
- a.out的由来
用过linux的都知道,在linux下编译链接程序,如果不加-o参数,生成的binary代码的名字都是默认的a.out.一不小心,a.out还会覆盖上次其他code生成的binary代码. a.out ...
- 论文解读(SDNE)《Structural Deep Network Embedding》
论文题目:<Structural Deep Network Embedding>发表时间: KDD 2016 论文作者: Aditya Grover;Aditya Grover; Ju ...
