GYM101471D「ICPC2017 WF」Money for Nothing

「ICPC2017 WF」Money for Nothing

传送门

我们可将生产商和消费商都看成二维平面上的点，其坐标分别为 \((d_i,p_i)\)，\((e_i,q_i)\)。

那么问题转变为：

给定平面上的 \(m\) 个 \(A\) 类点 \((d_i,p_i)\)，以及 \(n\) 个 \(B\) 类点 \((e_i,q_i)\)。求选择一个 \(A\) 类点作为矩形左下角，一个 \(B\) 类点作为矩形右上角所能得到的最大面积。若不存在这样的矩形就输出零。

考虑如下几种情况。

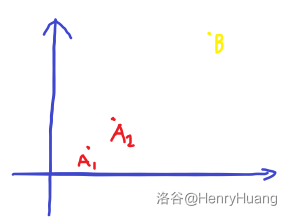
在这种情况下 \(A_1,A_2\) 都能与 \(B\) 围成一个矩形，但显然 \(A_1\) 更优秀。

故对于这样的 \(A\) 点我们可以直接舍弃。

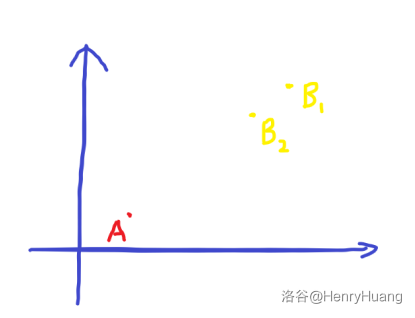
在这种情况下 \(B_1,B_2\) 都能与 \(A\) 围成一个矩形，但显然 \(B_1\) 更优秀。

故对于这样的 \(B\) 点我们可以直接舍弃。

舍弃掉这些点过后两种点在平面上的排布一定是这样的：

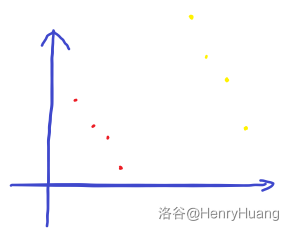
然后我们考虑这样一种情况：

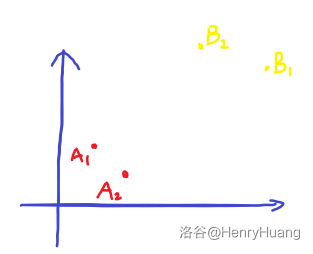
设 \(A_1,B_1\) 围成的矩形是以 \(A_1\) 为左下角的矩形当中最大的那一个。

我们可以得到这样一个结论：

\(A_2\) 和 \(B_2\) 围成的矩形的大小一定小于 \(A_2\) 和 \(B_1\) 围成的矩形的大小。

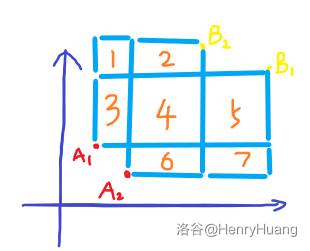
我们给这几个部分编个号，下面用编号代替上图中的部分。

根据我们前面的条件，有 \(3+4+5>3+4+1+2\rightarrow 5>1+2\)。

我们要证明的即 \(4+6+5+7>4+6+2\rightarrow 5+7>2\rightarrow 1+2+7> 2\)。

所以我们推广一下可以得到这样一个结论：对于每个红点，其围成最大矩形的黄点具有单调性。

根据这个性质我们直接分治就好了。

总时间复杂度为 \(O(n\log_2n)\)。

/*---Author:HenryHuang---*/
/*---Never Settle---*/
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=5e5+5;
struct cc{
	int x,y;
	LL operator*(const cc &h)const{
		return 1ll*(h.x-x)*(h.y-y);
	}
}a[maxn],b[maxn],p[maxn];
int sa,sb;
LL Ans;
void solve(int l,int r,int ll,int rr){
	if(l>r||ll>rr) return ;
	int mid=(l+r)>>1;
	LL ans=-1e18,id=0;
	for(int i=ll;i<=rr;++i){
		if(a[mid].x<b[i].x||a[mid].y<b[i].y){
			if(a[mid]*b[i]>ans){
				ans=a[mid]*b[i];
				id=i;
			}
		}
	}
	if(id!=0){
		solve(l,mid-1,ll,id);
		solve(mid+1,r,id,rr);
		Ans=max(Ans,ans);
	}

}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	int m,n;cin>>m>>n;
	for(int i=1;i<=m;++i){
		cin>>p[i].x>>p[i].y;
	}
	sort(p+1,p+m+1,[&](cc a,cc b){return a.x==b.x?a.y<b.y:a.x<b.x;});
	a[++sa]=p[1];
	for(int i=2;i<=m;++i){
		if(a[sa].y>p[i].y) a[++sa]=p[i];
	}
	for(int i=1;i<=n;++i){
		cin>>p[i].x>>p[i].y;
	}
	sort(p+1,p+n+1,[&](cc a,cc b){return a.x==b.x?a.y<b.y:a.x<b.x;});
	reverse(p+1,p+n+1);
	b[++sb]=p[1];
	for(int i=2;i<=n;++i){
		if(b[sb].y<p[i].y) b[++sb]=p[i];
	}
	reverse(b+1,b+sb+1);
	for(int i=1;i<=sb;++i) cout<<b[i].x<<' '<<b[i].y<<'\n';
	solve(1,sa,1,sb);
	cout<<Ans<<'\n';
	return 0;
}