【LeetCode】1102. Path With Maximum Minimum Value 解题报告 (C++)

• 作者： 负雪明烛
• id： fuxuemingzhu
• 个人博客：http://fuxuemingzhu.cn/

---

目录

• • 题目描述
  • 题目大意
  • 解题方法
  • • 排序+并查集
    • 优先级队列
  • 日期

题目地址：https://leetcode-cn.com/problems/path-with-maximum-minimum-value/

题目描述

Given a matrix of integers A with R rows and C columns, find the maximum score of a path starting at [0,0] and ending at [R-1,C-1].

The score of a path is the minimum value in that path. For example, the value of the path 8 → 4 → 5 → 9 is 4.

A path moves some number of times from one visited cell to any neighbouring unvisited cell in one of the 4 cardinal directions (north, east, west, south).

Example 1:

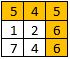
Input: [[5,4,5],[1,2,6],[7,4,6]]
Output: 4
Explanation:
The path with the maximum score is highlighted in yellow.

Example 2:

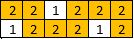
Input: [[2,2,1,2,2,2],[1,2,2,2,1,2]]
Output: 2

Example 3:

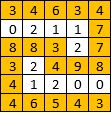
Input: [[3,4,6,3,4],[0,2,1,1,7],[8,8,3,2,7],[3,2,4,9,8],[4,1,2,0,0],[4,6,5,4,3]]
Output: 3

Note:

1. 1 <= R, C <= 100
2. 0 <= A[i][j] <= 10^9

题目大意

给你一个 R 行 C 列的整数矩阵 A。矩阵上的路径从 [0,0] 开始，在 [R-1,C-1] 结束。
路径沿四个基本方向（上、下、左、右）展开，从一个已访问单元格移动到任一相邻的未访问单元格。
路径的得分是该路径上的 最小 值。例如，路径 8 → 4 → 5 → 9 的值为 4 。
找出所有路径中得分 最高 的那条路径，返回其 得分。

解题方法

排序+并查集

参照1101. The Earliest Moment When Everyone Become Friends的做法，我们把图里面的每一个点按照值的大小顺序，依次遍历，如果某个点的与其四联通的某个点已经被访问过，那么把这两个点所属的子图连接成为一个图。一直遍历到左上角的位置和右下角的位置属于同一个图为止，此时就是就是题目要求的首尾相接。

帮助理解的几个点：

1. 题目的意思是路径上最小的点，并不是最短路径，所以按照值的大小进行排序。
2. 已经完成了按值的排序，所以会把图里面值最大的点优先访问。
3. 每次新遍历一个点的时候，检查周围的点是否已经访问过（值更大），把该点放入周围的图中。
4. 值最大的点不一定在一起，因此会形成多个子图。
5. 直到添加了一个较小的点时，起终两点联通了，那么这个新添加的点就是我们要求的。

C++代码如下：

class Solution {
public:
    int maximumMinimumPath(vector<vector<int>>& A) {
        const int M = A.size();
        const int N = A[0].size();
        const int X = M * N;
        parent = vector<int>(X, 0);
        for (int i = 0; i < parent.size(); ++i)
            parent[i] = i;
        vector<vector<int>> values;
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                values.push_back({A[i][j], i, j});
            }
        }
        sort(values.begin(), values.end(), [](vector<int>& a, vector<int>& b) {return a[0] < b[0];});
        unordered_set<int> visited;
        visited.insert(0);
        visited.insert(X - 1);
        int res = min(A[0][0], A[M - 1][N - 1]);
        while(find(0) != find(X - 1)) {
            vector<int> cur = values.back(); values.pop_back();
            visited.insert(cur[1] * N + cur[2]);
            res = min(res, cur[0]);
            for (auto& dir : dirs) {
                int newx = cur[1] + dir[0];
                int newy = cur[2] + dir[1];
                if (newx >= 0 && newx < M && newy >= 0 && newy < N && visited.count(newx * N + newy)) {
                    uni(cur[1] * N + cur[2], newx * N + newy);
                }
            }
        }
        return res;
    }
    int find(int a) {
        if (parent[a] == a)
            return a;
        return find(parent[a]);
    }
    void uni(int a, int b) {
        int pa = find(a);
        int pb = find(b);
        if (pa == pb)
            return;
        parent[pa] = pb;
    }
private:
    vector<int> parent;
    vector<vector<int>> dirs = {{0, 1}, {0, -1}, {-1, 0}, {1, 0}};
};

优先级队列

这个做法的思路应该更常规一点，是我想到的第一个解法，即从起点开始进行搜索，把其周围的所有点都放入大根堆中。遍历时，优先搜索值比较大的点，并把该点周围的所有点放入堆中，直至遇到了终点。

这个做法非常类似于Prim算法，Prim算法是从一个点开始，每次选择已访问过的所有点周围的没有访问过的点中距离最小的点。这个题反其道而行之，每次选择已访问过的所有点周围的没有访问过的点中值最大的点。

需要注意的是，会把每个点周围的所有点放入堆中，堆会进行排序，下次选择的仍然是到目前为止可以访问的值最大的点。举例说明：

[[6, 6, 0],
 [3, 0, 0],
 [3, 3, 3]]

 起始时把[0,1]位置的6和[1,0]位置的3都放入堆中。
 第一次会选择[0,1]位置的6，
 但是由于其周围的全是0，0放入堆中排到了后面，
 所以第二次访问的是[1,0]位置的3.

C++代码如下：

class Solution {
public:
    int maximumMinimumPath(vector<vector<int>>& A) {
        int R = A.size();
        int C = A[0].size();
        vector<vector<int> > visited(R, vector<int>(C, false));
        visited[0][0] = true;
        priority_queue<Point> pq;
        pq.push(Point(0, 0, A[0][0]));
        int res = min(A[0][0], A[R - 1][C - 1]);
        while (!pq.empty()) {
            Point p = pq.top();
            pq.pop();
            for (int i = 0; i < 4; ++i) {
                int r = p.x + dirs[i][0];
                int c = p.y + dirs[i][1];
                if (r >= 0 && r < R && c >= 0 && c < C && !visited[r][c]) {
                    res = min(res, p.val);
                    if (r == R - 1 && c == C - 1) return res;
                    visited[r][c] = true;
                    pq.push(Point(r, c, A[r][c]));
                }
            }
        }
        return res;
    }
private:
    struct Point {
        int x, y, val;
        Point(int _x, int _y, int _val) : x(_x), y(_y), val(_val) {}
        bool operator < (const Point& other) const {
            return this->val < other.val;
        }
    };
    int dirs[4][2] = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
};

参考资料：
https://leetcode-cn.com/problems/path-with-maximum-minimum-value/solution/pai-xu-bing-cha-ji-python3-by-smoon1989-2/
https://leetcode-cn.com/problems/path-with-maximum-minimum-value/solution/c-you-xian-dui-lie-by-da-li-wang-2/

日期

2019 年 9 月 23 日 —— 昨夜睡的早，错过了北京的烟火