Haar小波分析
一 尺度函数与小波函数
基本尺度函数定义为: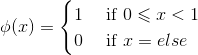 ,对其向右平移任意 k 个单位,构成函数族
,对其向右平移任意 k 个单位,构成函数族 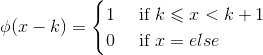 , 该函数族在
, 该函数族在 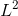 空间中正交,证明如下:
空间中正交,证明如下:
1 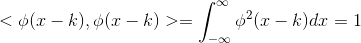 ;
;
2 当 m 不等于 k 时,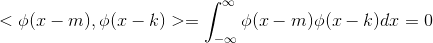
函数族 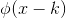 构成一组正交基,并形成
构成一组正交基,并形成  子空间。在
子空间。在  子空间中,任意函数均可表示为
子空间中,任意函数均可表示为  的线性组合,
的线性组合,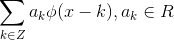 。
。
将函数族  构造宽度缩小一半,则可形成宽度为
构造宽度缩小一半,则可形成宽度为  的一组正交基,
的一组正交基,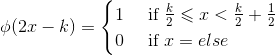 ,同样,该函数族在
,同样,该函数族在 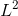 空间中正交,并形成
空间中正交,并形成 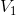 子空间。在
子空间。在 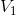 子空间中,任意函数均可表示为
子空间中,任意函数均可表示为 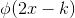 的线性组合,
的线性组合,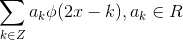 。
。
通过以上举例可得:设 j 为非负整数,j 级函数子空间可表示为 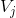 ,其对应正交基包括:
,其对应正交基包括:
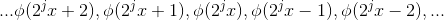 ,观察
,观察 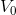 中
中 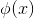 可有
可有 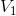 中
中  线性组合(
线性组合(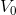 中任意函数均可用
中任意函数均可用 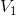 中函数线性组合表达),则
中函数线性组合表达),则 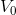 为
为 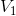 得子空间。各个子空间之间存在如下关系:
得子空间。各个子空间之间存在如下关系: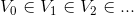 。
。
使用不同子空间 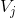 中尺度函数得线性组合,可以阶梯近似任意连续函数。在噪声滤除应用中,需要提取一些属于
中尺度函数得线性组合,可以阶梯近似任意连续函数。在噪声滤除应用中,需要提取一些属于 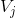 (高频信息)但不属于
(高频信息)但不属于 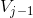 (低频信息)的方法,小波函数即描述了这部分信息,也即小波函数描述
(低频信息)的方法,小波函数即描述了这部分信息,也即小波函数描述  相对于
相对于 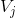 的正交补空间。根据以上描述,小波函数应该满足一些特性:
的正交补空间。根据以上描述,小波函数应该满足一些特性:
1 小波函数仍然位于 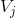 空间中,则他应该是
空间中,则他应该是 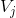 空间基函数的线性组合;
空间基函数的线性组合;
2 小波函数位于 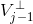 子空间中,则它应于
子空间中,则它应于 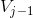 正交。
正交。
 空间的基本小波函数表示为:
空间的基本小波函数表示为: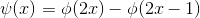 ,该函数位于
,该函数位于 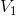 空间,且与
空间,且与 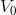 正交。同样对小波函数向右平移 k 个单位,构成函数族:
正交。同样对小波函数向右平移 k 个单位,构成函数族:
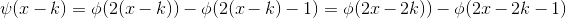 ,该函数族在
,该函数族在 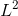 空间中正交。
空间中正交。
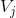 空间的基本小波函数表示为:
空间的基本小波函数表示为: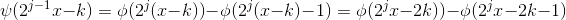 ,该函数族在
,该函数族在 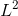 空间中正交。
空间中正交。
使用尺度函数与小波函数,可以将 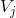 空间中函数进行分解:
空间中函数进行分解: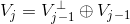 ,其中
,其中 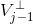 为
为 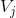 空间中的小波函数,继续以上分解,可得:
空间中的小波函数,继续以上分解,可得:
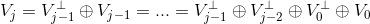
二 Haar分解
1 将函数离散化为 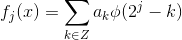 ,该函数位于
,该函数位于 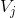 空间中;
空间中;
2 由于 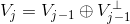 ,可以将
,可以将 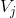 空间中该函数分解为
空间中该函数分解为 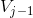 (更平滑尺度函数) 与
(更平滑尺度函数) 与 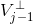 (小波函数),根据尺度函数与小波函数定义,有如下关系:
(小波函数),根据尺度函数与小波函数定义,有如下关系:
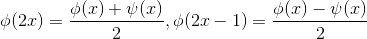 (根据图形可验证结论正确),进一步有:
(根据图形可验证结论正确),进一步有:
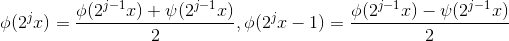 ;
;
3 观察到 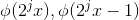 分解方式不一致,需要将原函数改写为:
分解方式不一致,需要将原函数改写为: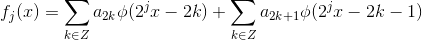 ;
;
4 对改写后的 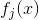 分别使用更平滑尺度函数与对应小波函数再次改写,有:
分别使用更平滑尺度函数与对应小波函数再次改写,有:
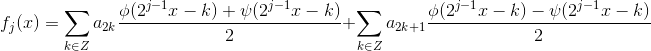 ,整理得:
,整理得:
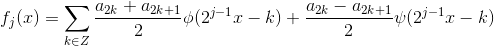 ;
;
5 令 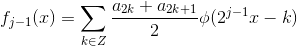 ,继续分解直到
,继续分解直到 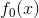 ,可得:
,可得:
 ,其中,
,其中,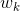 为相应的小波分量。
为相应的小波分量。
三 Haar重构
1 函数被分解为  , 其中,
, 其中,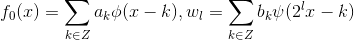 ;
;
2 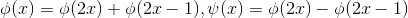 (根据图形可验证结论正确),进一步有:
(根据图形可验证结论正确),进一步有:
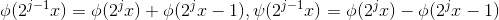
3 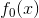 重构为
重构为 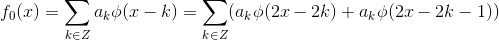 ;
;
4 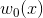 重构为
重构为 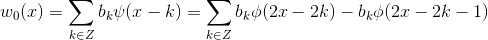 ;
;
5 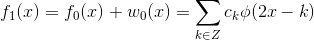 , 其中,
, 其中, 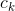 由
由 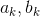 组合;
组合;
6 继续重构 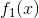 与
与  ,直到重构
,直到重构  。
。
参考资料 小波与傅里叶分析基础 Albert Boggess & Francis J. Narcowich
Haar小波分析的更多相关文章
- 图像算法五:【图像小波变换】多分辨率重构、Gabor滤波器、Haar小波
原 https://blog.csdn.net/alwaystry/article/details/52756051 图像算法五:[图像小波变换]多分辨率重构.Gabor滤波器.Haar小波 2018 ...
- Haar小波的理解
1. 首先理解L^2(R)的概念 L^2(R) 是一个内积空间的概念,表示两个无限长的向量做内积,张成的空间问题.也就是两个函数分别作为一个向量,这两个函数要是平方可积的.L^2(a,b)=<f ...
- 特征检测之Haar
Harr特征, 主要用于人脸检测,可以参考我的博文 基于MATLAB的adaboost级联形式的人脸检测实现 1 harr特征的原理 2 haar特征的计算 3 haar特征的应用
- 浅谈人脸检测之Haar分类器方法
我们要探讨的Haar分类器实际上是Boosting算法(提升算法)的一个应用,Haar分类器用到了Boosting算法中的AdaBoost算法,只是把AdaBoost算法训练出的强分类器进行了级联,并 ...
- OpenCv haar+SVM训练的xml检测人头位置
注意:opencv-2.4.10 #include "stdio.h"#include "string.h"#include "iostream&qu ...
- opencv - haar人脸特征的训练
step 1: 把正样品,负样品,opencv_createsamples,opencv_haartraining放到一个文件夹下面,利于后面的运行.step 2: 生成正负样品的描述文件 正样品描述 ...
- 图像特征提取三大法宝:HOG特征,LBP特征,Haar特征(转载)
(一)HOG特征 1.HOG特征: 方向梯度直方图(Histogram of Oriented Gradient, HOG)特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子.它通过计算和 ...
- Haar特征
转自:http://blog.csdn.net/carson2005/article/details/8094699 Haar-like特征,即很多人常说的Haar特征,是计算机视觉领域一种常用的特征 ...
- 浅析人脸检测之Haar分类器方法
一.Haar分类器的前世今生 人脸检测属于计算机视觉的范畴,早期人们的主要研究方向是人脸识别,即根据人脸来识别人物的身份,后来在复杂背景下的人脸检测需求越来越大,人脸检测也逐渐作为一个单独的研究方向发 ...
随机推荐
- Linux sudo 找不到命令
普通用户执行需要root权限的命令,提示"找不到命令",但是root用户执行该命令不报错,可能是由于该命令未处在sudo搜索的路径. 本文以sudo easy_install 为例 ...
- spring cloud --- Zuul --- 心得
spring boot 1.5.9.RELEASE spring cloud Dalston.SR1 1.前言 什么是 Zuul? Zuul是微服务网关,与Gateway类似 ,根据请 ...
- Linux上天之路系列目录
Linux上天之路系列目录 Linux上天之路(一)之Linux前世今生 Linux上天之路(二)之Linux安装 Linux上天之路(三)之Linux系统目录 Linux上天之路(四)之Linux界 ...
- 老旧业务重构案例——IM系统如何设计
一年半之前刚来到这个团队,便遭遇了一次挑战: 当时有个CRM系统,老是出问题,之前大的优化进行了4次小的优化进行了10多次,要么BUG重复出现,要么性能十分拉胯,总之体验是否糟糕!技术团队因此受到了诸 ...
- 51 Nod 1133 不重叠的线段 (贪心算法)
原题链接:https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1133 题目分析:感觉这到第不应该被分到二级算法题,比 109 ...
- elasticsearch之拼音搜索
拼音搜索在中文搜索环境中是经常使用的一种功能,用户只需要输入关键词的拼音全拼或者拼音首字母,搜索引擎就可以搜索出相关结果.在国内,中文输入法基本上都是基于汉语拼音的,这种在符合用户输入习惯的条件下缩短 ...
- java 报错: MalformedURLException: unknow protocol: f
问题: java 使用 URL 读取文件解读报错 MalformedURLException 1.使用 URL对象解析文件报错MalformedURLException: unknow protoco ...
- 为什么JavaWeb要分层
首先bai让我们坐着时光机回到n年前的web开发.那个时候最早du都是静态的html页面,zhi后来有了数据库,有了所谓dao的动态页面,然后程序猿在编码的时候,会把所有的代码都写在页面上,包括数据库 ...
- lua之自索引
Father={ a=100, b=200 } function Father:dis() print(self.a,self.b) end Father.__index=Father Son= { ...
- golang中的tcp编程
1. tcp server package main import ( "bufio" "fmt" "net" ) func main() ...
