洛谷p3385【模板】负环

最近很久没怎么写最短路的题导致这个题交了好多遍

AC率是怎么下来的自己心里没点数

SPFA虽然臭名昭著但是他可以用来判负环

如果一个点进队的次数大于等于n说明存在负环

这道题一开始memset我给dis赋了零

在SPFA厨师第一个点的时候根本就忘了还要初始化dis

菜死了

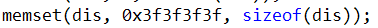
还有这题变态没让着输出YES或者NO

他让着输出YE5和N0......虽然我一眼就看出来了但是我还是把E写成了小写的....

Code：

//SPFA判断负环
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N = ;
int head[N << ], n, m, cnt, tim[N], T, dis[N];
struct node {
    int nxt, to, w;
}e[N << ];
bool vis[N];
int read() {
    int s = , w = ;
    char ch = getchar();
    while(!isdigit(ch)) {if(ch == '-') w = -; ch = getchar();}
    while(isdigit(ch)) {s = s *  + ch - ''; ch = getchar();}
    return s * w;
}
void add(int x, int y, int z) {
    e[++cnt].nxt = head[x];
    e[cnt].to = y;
    e[cnt].w = z;
    head[x] = cnt;
}
bool  spfa() {
    queue<int> q;
    q.push();
    vis[] = ;
    dis[] = ;
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        vis[u] = ;
        for(int i = head[u]; i; i = e[i].nxt) {
            int v = e[i].to;
            if(dis[v] > dis[u] + e[i].w) {
                dis[v] = dis[u] + e[i].w;
                if(!vis[v]) {
                    tim[v]++;
                    q.push(v);
                    vis[v] = ;
                    if(tim[v] >= n) return ;
                }
            }
        }
    }
    return ;
}
int main() {
    T = read();
    while(T--) {
        memset(vis, , sizeof(vis));
        memset(head, , sizeof(head));
        memset(tim, , sizeof(tim));
        memset(dis, 0x3f3f3f3f, sizeof(dis));
        n = read(), m = read();
        for(int i = , x, y, z; i <= m; i++) {
            x = read(), y = read(), z = read();
            if(z < ) add(x, y, z);
            else add(x, y, z), add(y, x, z);
        }
        if(spfa()) printf("YE5\n");
        else printf("N0\n");
    }
    return ;
}