打家劫舍I

题目描述(LeetCode)

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

示例 1:

输入: [,,,]
输出:
解释: 偷窃  号房屋 (金额 = ) ，然后偷窃  号房屋 (金额 = )。
     偷窃到的最高金额 =  +  =  。

示例 2:

输入: [,,,,]
输出:
解释: 偷窃  号房屋 (金额 = ), 偷窃  号房屋 (金额 = )，接着偷窃  号房屋 (金额 = )。
     偷窃到的最高金额 =  +  +  =  。

题目讲解

很多人拿到上面的意思,可能还是没有理解透彻,讲解一下思路:

• 标签: 动态规划
• 动态规划方程: dp[n] = MAX( dp[n-1], dp[n-2] + num )
• 由于不可以在相邻的房屋闯入,所以在当前位置n房屋可盗窃的最大值,要么就是 n-1 房屋可盗窃的最大值，要么就是 n-2 房屋可盗窃的最大值加上当前房屋的值，二者之间取最大值
• 举例说明: 1号房间可盗窃的最大值为3,即为dp[1] = 3, 2号房间可盗窃最大值为4,即为dp[2] = 4, 3号公寓自身为2,即为num=2,那么 dp[3] = MAX( dp[2], dp[1] + num ) = MAX(4, 3+2) = 5,3 号房间可盗窃最大值为 5
• 时间复杂度为: O(n), n为数组长度

下面我们通过图解,通过例子[3,1,2,4]来讲解:

2.1

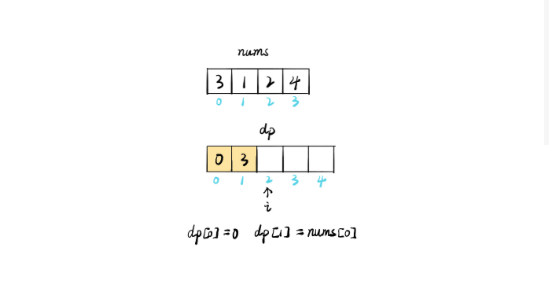
上面代表是举出例子,3,1,2,4,下面的代表是dp函数,也就是前面相加之和记为dp

开始dp[0] = 0,dp[1] = num[0]= 3

1/5

2.2

dp[0] = 0, dp[1] = 3, dp[i] = MAX(dp[i - 1], dp[i - 2] + num[i - 1] )---->dp[0],是从0开始

dp[2] = MAX(dp[1], dp[0] + num[i]) = MAX(3, 0 + 1) = 3

所以dp[2] = 3

2.3

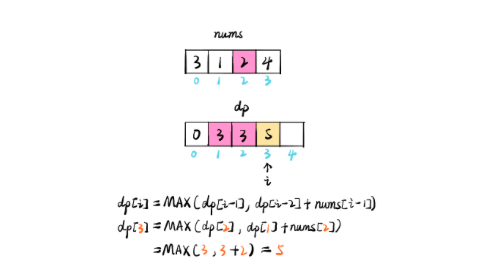
dp[0] = 0, dp[1] = 3, dp[i] = MAX(dp[i - 1], dp[i - 2] + num[i - 1] )---->dp[0],是从0开始

dp[3] = MAX(dp[2], dp[1] + num[2]) = MAX(3, 3 + 2) = 5

所以dp[3] = 5

2.4

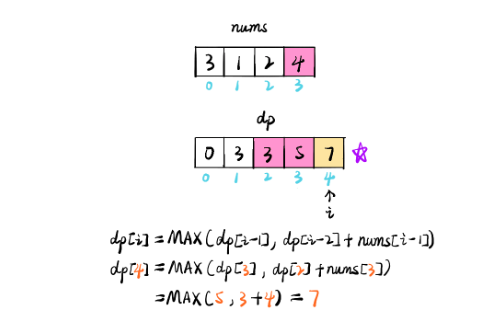
dp[0] = 0, dp[1] = 3, dp[i] = MAX(dp[i - 1], dp[i - 2] + num[i - 1] )---->dp[0],是从0开始

dp[4] = MAX(dp[3], dp[2] + num[3]) = MAX(5, 3 + 4) = 7

所以dp[4] = 7

题目代码

(1)针对上面的思路分析,下面是java 代码

class Solution {
    public int rob(int[] nums) {
        int len = nums.length;
        if(len == )
            return ;
        int[] dp = new int[len + ];
        dp[] = ;
        dp[] = nums[];
        for(int i = ; i <= len; i++) {
            dp[i] = Math.max(dp[i-], dp[i-] + nums[i-]);
        }
        return dp[len];
    }
}

(2)swift代码如下(可在playground直接运行)

let numsArr: [Int] = [,,,]
var newNumArr = [Int]()
func robs(numArr: [Int]) -> Int {
    if numArr.count ==  {
        return
    }
　　//newNumArr[0] = 0这种写法是错误的,swift数组不允许直接赋值,会造成两个数组同时操作同一块地址空间
    newNumArr.append(0)
    newNumArr.append(numArr[0])
    var fk_1 =
    var fk_2 =
    for i in ..<(numArr.count + ) {
        fk_1 = newNumArr[i - ]
        fk_2 = newNumArr[i - ] + numArr[i - ]
        let temp = fk_1 > fk_2 ? fk_1 : fk_2
        newNumArr.append(temp)
    }
    return newNumArr[numArr.count]

}
let maxRob = robs(numArr: numsArr)
print(maxRob)

输出结果是7,和上面一样!

上面是打家劫舍的第一版本,后续我们将继续出版其他版本的打家劫舍,欢迎大家关注,谢谢