51nod1790 输出二进制数

题目描述

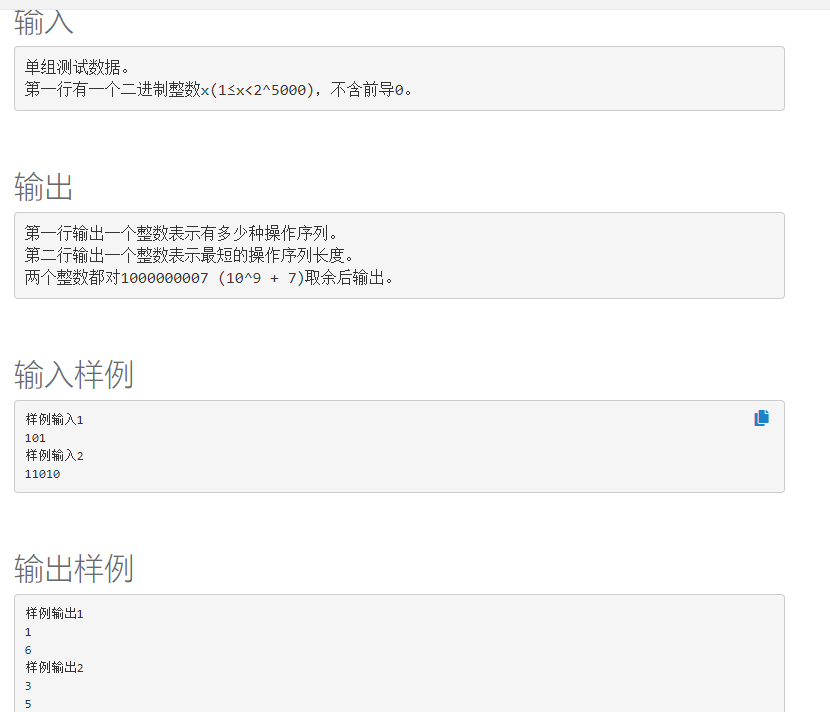
题解

过于真实

LJ卡常题

一个显然的dp：

设f[i][j]表示做完前i个，最后一段为j+1~i的方案（最小值同理）

那么f[i][j]=min(f[i-j-1][k])，其中k~j-1要小于j~i

这样做是n³的，而且不好判断二进制的大小

一个很显然的想法，把所有的状态丢到trie上转移，先按位数（深度），再按字典序（先0后1）来转移

每次维护f[i]，表示当前以i结尾的方案，那么对于当前的f[i]加上f[i-长度]

因为连续多段相同的数，所以trie上每个点挂的状态要从小到大排（即反着加邻接表）

可以发现这样的实质是把所有状态按字典序转移，而且对于每个i和j，每个k只会被加一次

---

一些小(?)优化：

每个段的结尾的下一位必须要是1，不然没法往下接

f[i][j]如果j<n，那么要保证j-i+1≤n-j

---

trie的大小是n^{2的（每个后缀），状态总数也是n}2，所以理论复杂度是O(n^2)

加上上面的优化，在正常的评测机上跑不会有什么问题

然而——

由于51nod的神奇评测机，在本地&jzoj上跑1.1s（加了O2跑1.2s别问为什么变慢了），在51nod上跑了1.6s+

所以

你懂得

code

#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <bitset>
#define fo(a,b,c) for (register int a=b; a<=c; a++)
#define fd(a,b,c) for (register int a=b; a>=c; a--)
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define mod 1000000007
#define LEN 12502500
using namespace std;

char St[5002]={"你懂得"};
struct type{
	short int a[5003];
	int len;
} ans,a1,a2;
short int A[LEN+1];
int B[LEN+1];
int ls[LEN+1];
int tr[LEN+1][2];
int a[5001];
int d[2][5001];
int f[5001];
int g[5001];
int t[2];
int I,I2,n,i,j,k,l,sum,len,L,Ans;
char ch;
bool bz;

void add()
{
	register int i;

	if (a1.len>=a2.len)
	{
		a1.a[a1.len+1]=0;
		bz=0;

		fo(i,1,a2.len)
		{
			a1.a[i]+=a2.a[i];

			if (a1.a[i]>1)
			{
				a1.a[i]-=2;
				++a1.a[i+1];
			}
		}
		fo(i,a2.len+1,a1.len)
		if (a1.a[i]>1)
		{
			a1.a[i]-=2;
			++a1.a[i+1];
		}
		else
		break;

		if (a1.a[a1.len+1])
		++a1.len;
	}
	else
	{
		a2.a[a2.len+1]=0;
		bz=1;

		fo(i,1,a1.len)
		{
			a2.a[i]+=a1.a[i];

			if (a2.a[i]>1)
			{
				a2.a[i]-=2;
				++a2.a[i+1];
			}
		}
		fo(i,a1.len+1,a2.len)
		if (a2.a[i]>1)
		{
			a2.a[i]-=2;
			++a2.a[i+1];
		}
		else
		break;

		if (a2.a[a2.len+1])
		++a2.len;
	}
}

void cmp()
{
	register int i;

	if (!bz)
	{
		if (ans.len>a1.len)
		ans=a1;
		else
		if (ans.len==a1.len)
		{
			fd(i,ans.len,1)
			if (ans.a[i]>a1.a[i])
			{
				ans=a1;
				return;
			}
			else
			if (ans.a[i]<a1.a[i])
			return;
		}
	}
	else
	{
		if (ans.len>a2.len)
		ans=a2;
		else
		if (ans.len==a2.len)
		{
			fd(i,ans.len,1)
			if (ans.a[i]>a2.a[i])
			{
				ans=a2;
				return;
			}
			else
			if (ans.a[i]<a2.a[i])
			return;
		}
	}
}

void turn(register int t)
{
	while (t)
	{
		a2.a[++a2.len]=t&1;
		t>>=1;
	}
}

int main()
{
//	freopen("51nod_1790_35_in.txt","r",stdin);
//	freopen("51nod_1790_28_in.txt","r",stdin);
//	freopen("51nod_1790_15_in.txt","r",stdin);
//	freopen("51nod1790.in","r",stdin);

	ch=getchar();
	while (ch>='0' && ch<='1')
	{
		a[++n]=ch=='1';
		ch=getchar();
	}

	if (n==5000)
	{
		for (i=1; i<=n; ++i)
		if (St[i]!=a[i]+'0')
		break;

		if (i>n)
		{
			printf("gou li guo jia sheng si yi\n");
			printf("qi yin huo fu bi qu zhi\n");
			return 0;
		}
	}

	a[n+1]=1;

	l=0;
	len=1;
	fd(i,n,1)
	if (a[i])
	{
		k=1;
		fo(j,i,n)
		{
			if (!tr[k][a[j]])
			tr[k][a[j]]=++len;
			k=tr[k][a[j]];

			if (a[j+1] && (j-i+1<=n-j || j==n))
			{
				++L;
				A[L]=j;
				B[L]=ls[k];
				ls[k]=L;
			}
		}
	}

	memset(g,1,sizeof(g));
	f[0]=1;
	g[0]=0;
	ans.len=2333333;

	I=0;
	d[0][1]=1;
	t[0]=1;
	l=-1;
	while (t[I])
	{
		I2=I^1;
		t[I2]=0;
		++l;

		fo(i,1,t[I])
		{
			for (register int j=ls[d[I][i]]; j; j=B[j])
			{
				f[A[j]]=(f[A[j]]+f[A[j]-l])%mod;

				if (A[j]<n)
				g[A[j]]=min(g[A[j]],g[A[j]-l]+1);
				else
				if (g[A[j]-l]<=n && l<=ans.len)
				{
					a1.len=0;
					a2.len=0;

					fd(k,n,n-l+1)
					a1.a[++a1.len]=a[k];
					turn(g[A[j]-l]+1);

					add();
					cmp();
				}
			}

			if (tr[d[I][i]][0]) d[I2][++t[I2]]=tr[d[I][i]][0];
			if (tr[d[I][i]][1]) d[I2][++t[I2]]=tr[d[I][i]][1];
		}

		I=I2;
	}

	fd(i,ans.len,1)
	Ans=((Ans<<1)+ans.a[i])%mod;

	printf("%d\n",f[n]);
	printf("%d\n",Ans);
}