[CSP-S模拟测试]:party?（霍尔定理+最小割+树链剖分）

题目描述

$Treeland$国有$n$座城市，其中$1$号城市是首都，这些城市被一些单向高铁线路相连，对于城市$i\neq 1$，有一条线路从$i$到$p_i(p_i<i)$。每条线路都是一样长的，通过花费时间也是一样长的。
这个国家的每一个城市都有一种特产，整个国家有$m$种特产（不同城市可能又相同的特产），其中城市$i$的特产用$a_i$表示。
小$C$和他的几位$A$队爷朋友（总共$c$人，$2\leqslant c\leqslant 5$）正在$Treeland$国游玩，他们准备在一个城市进行$water party$。召开$party$的城市必须满足每个人从各自城市出发能尽快到齐。注意可能有人在同一个城市。
小$C$和他的朋友们准备各自带一些特产到$party$。这些特产必须满足以下条件：
    $\alpha.$每个人带的特产数量必须相同。
    $\beta.party$里不能够有任何两种相同的特产。
    $\gamma.$每个人只能带他所经过的城市的特产。
对于每个询问，计算出$party$中最多有多少种特产。

---

输入格式

第一行三个整数$n,m,q$，分别表示城市个数，特产种数，询问个数。
第二行有$n-1$个整数，表示$p_1,p_2,p_3,...,p_n$。
第三行有$n$个整数，表示$a_1,a_2,...,a_n$。
接下来$q$行，每行表示一个询问。每个询问第一个整数$c$表示人数，接下来有$c$个整数表示每一个人所在城市的编号。

---

输出格式

对于每个询问输出一行一个整数，表示答案。

---

样例

样例输入：

5 3 4
1 2 2 1
2 3 1 3 1
2 3 4
3 5 2 2
4 3 4 2 5
2 2 2

样例输出：

2
3
0
0

---

数据范围与提示

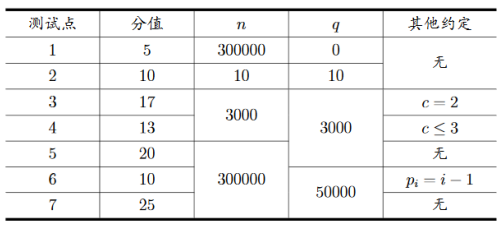
对于$100\%$的数据，满足：

$2\leqslant n\leqslant 300,000,1\leqslant m\leqslant 1,000,0\leqslant q\leqslant 50,000,1\leqslant p_i<i,1\leqslant a_i\leqslant m,2\leqslant c\leqslant 5$。

---

题解

延续上道题的思路，发现最多只有$5$个人，接着考虑网络流问题。

容易（我不容易）发现，从源点给每个人连一定容量的边（容量利用二分即可），每个人向他的颜色连边，颜色再向汇点连容量为$1$的边，能跑满则可行，求最小割即可。

接着运用霍尔定理简化问题，二分将城市拆成多少个点，然后看是否有完美匹配即可。

可以用$bitset+$树链剖分获取集合。

时间复杂度：$\Theta(\frac{n\log n\times m}{w})$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to,w;}e[300000];
int head[300001],cnt=1;
int fa[300001];
int n,m,q;
int a[300001];
int depth[300001],son[300001],size[300001],dfn[300001],wzc[300001],topp[300001];
int c[50001][10];
bitset<1024> bit1[300001],bit2[600001];
void add(int x,int y)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	head[x]=cnt;
}
void dfs1(int x)
{
	depth[x]=depth[fa[x]]+1;
	size[x]=1;
	for(int i=head[x];i;i=e[i].nxt)
	{
		dfs1(e[i].to);
		size[x]+=size[e[i].to];
		if(!son[x]||size[e[i].to]>=size[son[x]])
			son[x]=e[i].to;
	}
}
void dfs2(int x,int tp)
{
	dfn[x]=++cnt;
	wzc[cnt]=x;
	if(!tp)tp=x;
	topp[x]=tp;
	if(son[x])dfs2(son[x],tp);
	for(int i=head[x];i;i=e[i].nxt)
		if(e[i].to!=son[x])dfs2(e[i].to,0);
}
void dfs3(int x)
{
	if(x==topp[x])bit1[x].set(a[x]);
	else (bit1[x]=bit1[fa[x]]).set(a[x]);
	for(int i=head[x];i;i=e[i].nxt)
		dfs3(e[i].to);
}
int LCA(int x,int y)
{
	while(topp[x]!=topp[y])
	{
		if(depth[topp[x]]<depth[topp[y]])swap(x,y);
		x=fa[topp[x]];
	}
	return depth[x]<depth[y]?x:y;
}
void build(int l,int r)
{
	if(l==r)
	{
		bit2[(l+r)|(l!=r)].set(a[wzc[l]]);
		return;
	}
	int mid=(l+r)>>1;
	build(l,mid);
	build(mid+1,r);
	bit2[(l+r)|(l!=r)]=bit2[(l+mid)|(l!=mid)]|bit2[(mid+1+r)|(mid+1!=r)];
}
bitset<1024> ask(int l,int r,int L,int R)
{
	if(L<=l&&r<=R)return bit2[(l+r)|(l!=r)];
	int mid=(l+r)>>1;
	bitset<1024> res;
	if(L<=mid)res|=ask(l,mid,L,R);
	if(R>mid) res|=ask(mid+1,r,L,R);
	return res;
}
bitset<1024> query(int x,int lca)
{
	bitset<1024> res;
	while(topp[x]!=topp[lca])
	{
		res|=bit1[x];
		x=fa[topp[x]];
	}
	res|=ask(1,n,dfn[lca],dfn[x]);
	return res;
}
int main()
{
	scanf("%d%d%d",&n,&m,&q);
	for(int i=2;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		add(x,i);
		fa[i]=x;
	}
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	cnt=0;
	dfs1(1);
	dfs2(1,0);
	for(int i=1;i<=q;i++)
	{
		scanf("%d",&c[i][0]);
		for(int j=1;j<=c[i][0];j++)
			scanf("%d",&c[i][j]);
	}
	dfs3(1);
	build(1,n);
	for(int i=1;i<=q;i++)
	{
		bitset<1024> set[10];
		int lca=LCA(c[i][1],c[i][2]);
		for(int j=3;j<=c[i][0];j++)lca=LCA(lca,c[i][j]);
		for(int j=1;j<=c[i][0];j++)
			set[j]=query(c[i][j],lca);
		int ans=m;
		for(int s=1;s<(1<<c[i][0]);s++)
		{
			int cnt=0;
			set[0].reset();
			for(int j=0;j<c[i][0];j++)
				if(s&(1<<j))
				{
					set[0]|=set[j+1];
					cnt++;
				}
				ans=min(ans,(int)set[0].count()/cnt);
		}
		printf("%d\n",ans*c[i][0]);
	}
	return 0;
}

---

rp++