Adaptive Synchronization of Dynamics on Evolving Complex Networks

原文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.100.114101

发表在：PRL 2008

--------------------------------------------------------------------------------------------------------------------------------------------------------------------

传统的模型的coupling的形式，

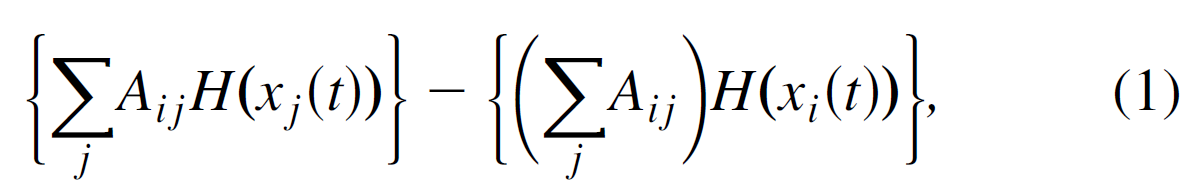
其中，A_ij 代表j到i的coupling强度，A_ii=0, x_i(t)是对应节点i的n维状态变量，H:Rⁿ --> Rⁿ,  一共有N个节点。

假设：对于节点i，

　　a. （1）式的第一项是可观测的信号，定义该信号为，

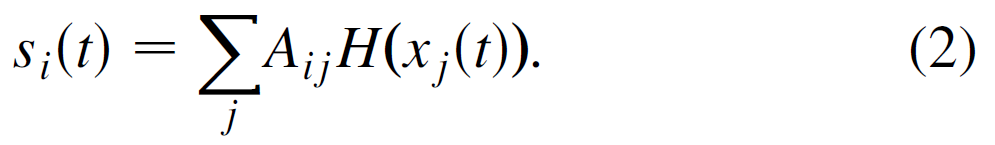　　b. 不知道输入的强度和，i.e., ∑_j A_ij.

接下来考虑下面的形式，

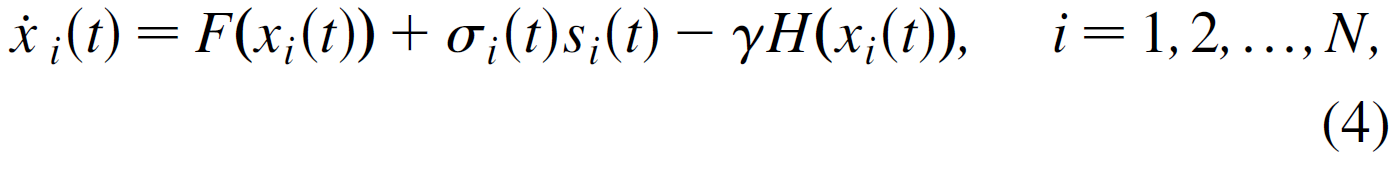
γ：constan gain 对于所有的节点. 同步解，

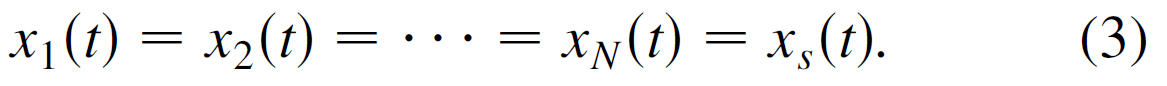
存在， 当σ_i(t) 等于

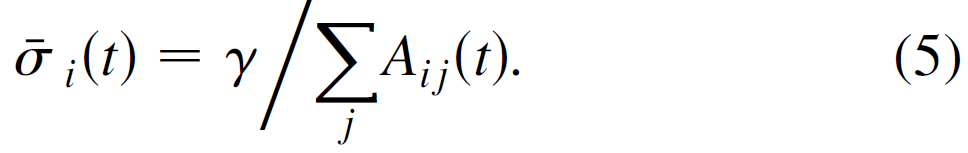
注意到，当

式子（4）可以写成，

其中

并且行和都等于0. 如果存在同步解，那么（7）式的最后一项就恒等于0. 动力学方程就变成了没有coulping的形式，

在这种情况下，根据master stability function theory， 同步解的稳定性可以通过选取合适的couping γ 保证.

需要注意的是，如果σ_i(t)  不满足（5）式，就不能保证同步解的稳定性了。下面将试着去如何设计σ_i(t)  ， 并且我们事先假设选取的 γ 能够使得同步解在σ_i(t)  满足（5）式时是稳定的。

在给出具体σ_i(t)的设计之前，对于节点i，我们先定义一个量，

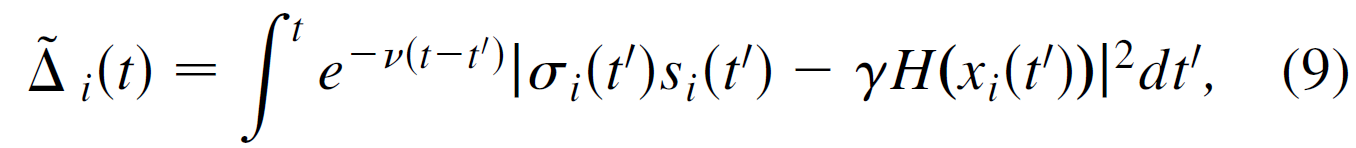
并且选择ν满足，

其中τ_S和τ_N分别是节点动力系统x_i(t)的time scale，网络结构A_ij(t)的time scale. 有了上面的这个假设，（9）式中σ_i(t') 就可以用σ_i(t) 代替(我没怎么看出来。。)，从而近似（9）式，得到，

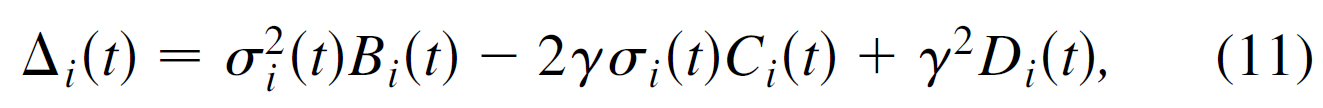
其中

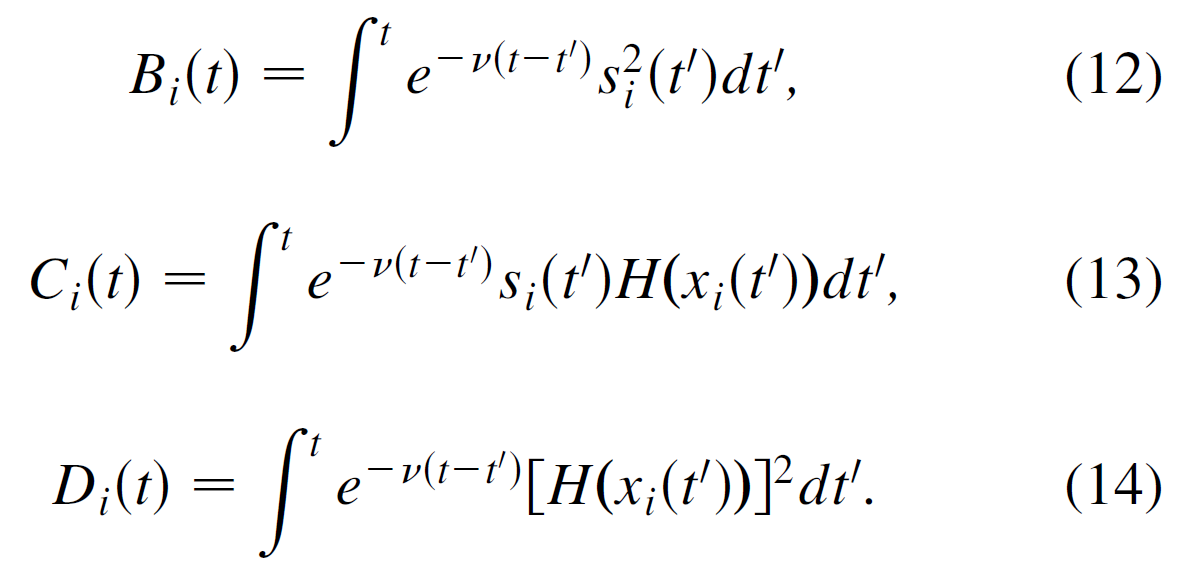
对于（9）式，如果等于0，那么就是同步，所以可以通过梯度下降的方法求近似解Δ_i的最小值，即，

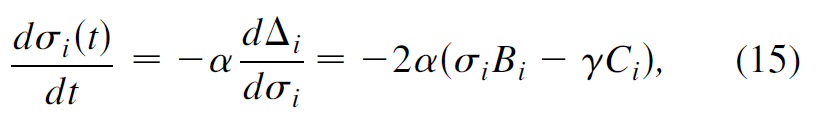
其中α是可调参数。 未来避免（12）和（13）式算积分，将其写成ODE的形式如下，

综上，设计的adaptive 策略可以用一组微分方程表示，i.e., 式子（4），（11），（15），（16）.

实验

考虑一个N个节点的随机网络，<k>N/2 条无向边，<k>是平均度。对于t=0时候，如果节点i和节点j有边，那么邻接矩阵A_ij(0)=A_ji(0)=1,否则A_ij(0)=0. 当t>0的时候，假设网络的演化为，

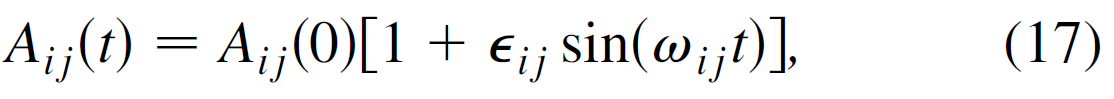
. 并且网络的时间尺度τ_N=(ω_max )^-1, much longer than 节点动力学的时间尺度τ_S，i.e.,  τ_N>τ_S,

考虑Rossler oscillators，

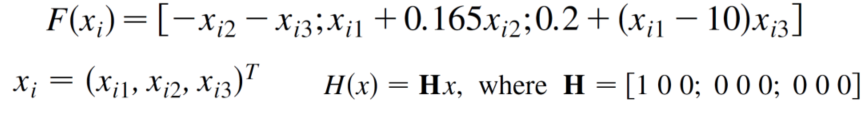
为了简单起见，假设自适应过程（15）非常快. 让α→oo, 那么 σ_i(t) 快速收敛到γC_i(t)/B_i(t). 这样子，我们可以之间把（11）式子替换成，

v以及C_i,B_i的初值对动力学是至关重要的。假设A_ij(0)是已知的，我们让C_i(0)=B_i(0)×[Σ_jAij(0)]^-1, 从而能够在初始时刻满足式子(6).

因为耦合系统可能存在其它的吸引子，我们希望设计合适的初值B_ij(0)，使得一开始耦合系统就落在同步解的吸引域中。为此，我们假设已经在同步解(8)上了，对式子（16）在时间轴上取平均，得到近似，B_i ≈ <s_i²>, 根据这个例子H(x)=(x, 0, 0)T, 我们有<s_i²>≈<k²><x_S1²>_t,  其中<x_S1²>_t是同步解（8）x_S1(t)在时间轴上的平均， 即，

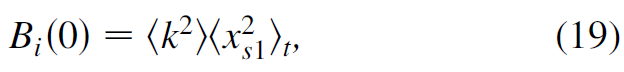
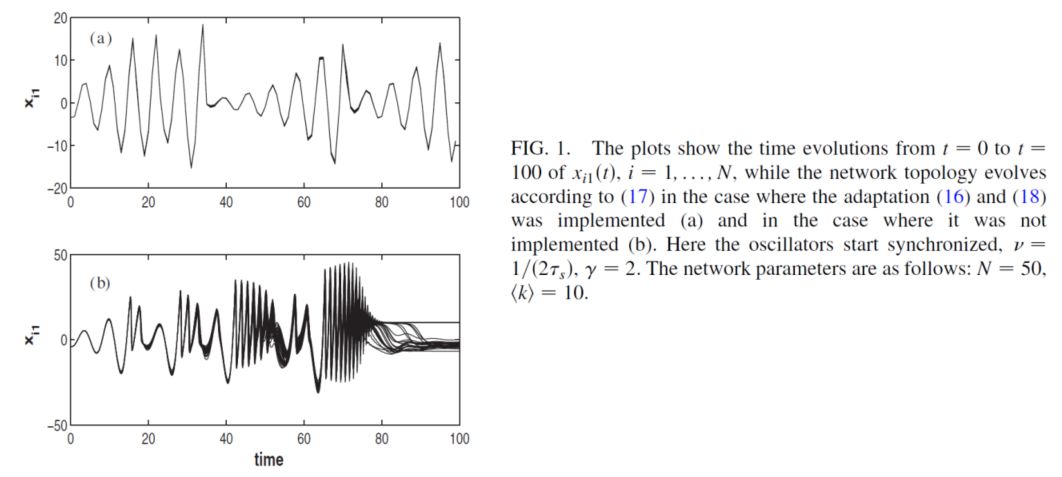
下面是数值结果，Figure 1(a)显示的是adaption (（16）和（18），（17）)的结果，几乎50个节点的演化轨迹都是一样的(几乎重合了) . Fig. 1(b)是没有adaption的结果， i.e.,