1233: [Usaco2009Open]干草堆tower

传送门

感觉正着做不太好搞，考虑倒过来搞

容易想到贪心，每一层都贪心地选最小的宽度，然后发现 $WA$ 了...

因为一开始多选一点有时可以让下一层宽度更小

然后有一个神奇的结论，最高的方案一定有一种是底层最窄的方案

证明：

考虑把所有块按顺序排成一排并分成几段，每一段都表示一层，假设如图是一种底层最窄的方案

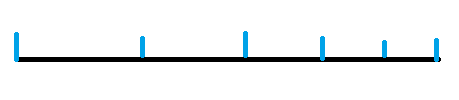
假设有一种更优的方案，使得底层更宽：

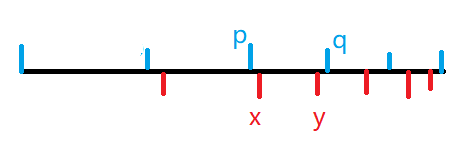
那么根据抽屉原理，蓝色至少一段中间一定有两个的红色分割线

不妨找到这样一个位置，标记为 $x,y$ ：

那么我们显然可以构造一个新的方案，使得上面几层按 $y$ 之后红色的分割，下面几层按 $p$ 之前蓝色的分割，中间一层是 $[p,y]$

因为 $[p,y]$ 比 $[x,y]$ 大，所以更上层也一定小于 $[p,y]$，同理 $[p,y]$ 一定小于 $[p,q]$ ，所以下层一定大于 $[p,y]$

然后发现我们构造的新方案变成了层数更多，底层仍然最窄的方案

所以证明了底层最窄的方案一定有一种是最优方案

然后就可以 $dp$ 了，设 $f[i]$ 表示考虑完 $i,n$ 的块时，底层最窄的宽度，同时维护 $g[i]$ 表示考虑完 $i,n$ 的块，底层最窄时的最大层数

那么显然枚举所有 $j>i$ ，转移 $f[i]=min(sum[j-1]-sum[i])$（$sum$ 是块宽度的前缀和）并且满足 $sum[j-1]-sum[i]>=f[j]$

然后发现对于两个决策 $k,j$ 其中 $k>j$，$k$ 会比 $j$ 更优仅当 $j$ 此时不合法，即 $sum[j-1]-sum[i]<f[j]$

又因为 $sum[i]$ 单调不增，所以合法决策点只会越来越小，所以用一个单调队列维护一波就可以做到 $O(n)$ 的转移了

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
typedef long long ll;
using namespace std;
inline ll read()
{
    ll x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const int N=2e5+;
int n,a[N],ans,g[N],Q[N];
ll sum[N],f[N];
// f[i]=sum[j-1]-sum[i-1] j>i sum[j-1]-sum[i-1]>=f[j]
// sum[i-1]<=sum[j-1]-f[j]
// k>j sum[k-1]-f[k]>sum[j-1]-f[j]
int main()
{
    n=read();
    for(int i=;i<=n;i++) a[i]=read();
    for(int i=;i<=n;i++) sum[i]=sum[i-]+a[i];
    int L=,R=; Q[]=n+;
    for(int i=n;i;i--)
    {
        while(L<R&&sum[Q[L+]-]-sum[i-]>=f[Q[L+]]) L++;//队列中越后面的位置越优
        f[i]=sum[Q[L]-]-sum[i-]; g[i]=g[Q[L]]+;
        while(L<=R&&sum[Q[R]-]-f[Q[R]]<=sum[i-]-f[i]) R--;
        Q[++R]=i;
    }
    printf("%d\n",g[]);
    return ;
}