抽象语法树简介(ZZ)

转载自：

http://www.cnblogs.com/cxihu/p/5836744.html

(一)简介

抽象语法树（abstract syntax code，AST）是源代码的抽象语法结构的树状表示，树上的每个节点都表示源代码中的一种结构，这所以说是抽象的，是因为抽象语法树并不会表示出真实语法出现的每一个细节，比如说，嵌套括号被隐含在树的结构中，并没有以节点的形式呈现。抽象语法树并不依赖于源语言的语法，也就是说语法分析阶段所采用的上下文无文文法，因为在写文法时，经常会对文法进行等价的转换（消除左递归，回溯，二义性等），这样会给文法分析引入一些多余的成分，对后续阶段造成不利影响，甚至会使合个阶段变得混乱。因些，很多编译器经常要独立地构造语法分析树，为前端，后端建立一个清晰的接口。

抽象语法树在很多领域有广泛的应用，比如浏览器，智能编辑器，编译器。

(二)抽象语法树实例

(1)四则运算表达式

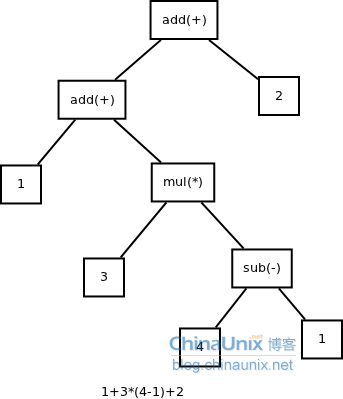
表达式: 1+3*(4-1)+2

抽象语法树为：

(2)xml

代码2.1：

1. <letter>
2. <address>
3. <city>ShiChuang</city>
4. </address>
5. <people>
6. <id>12478</id>
7. <name>Nosic</name>
8. </people>
9. </letter>

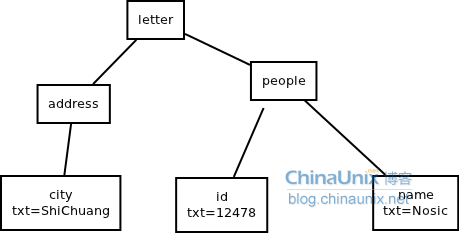
抽象语法树：

(3)程序1

代码2.2

1. while b != 0
2. {
3. if a > b
4. a = a-b
5. else
6. b = b-a
7. }
8. return a

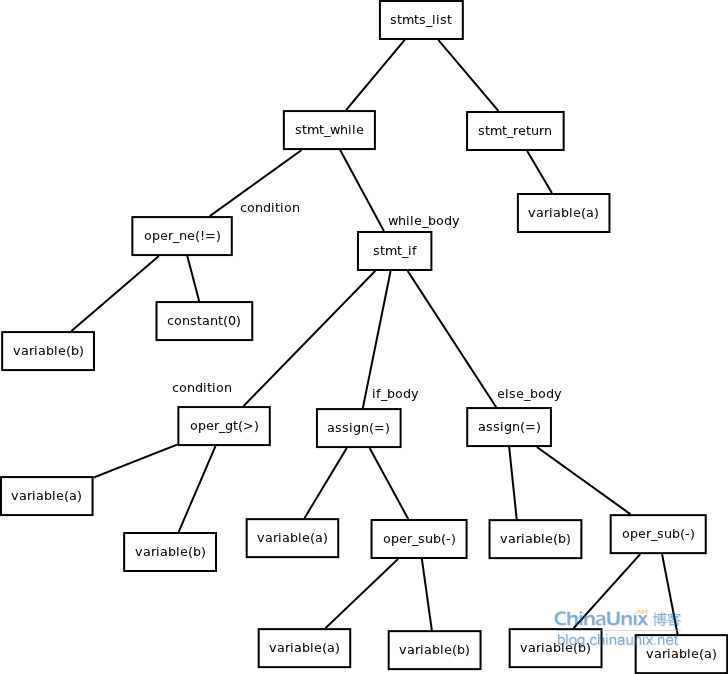
抽象语法树：

(4)程序2

代码2.3

1. sum=0
2. for i in range(0,100)
3. sum=sum+i
4. end

抽象语法树

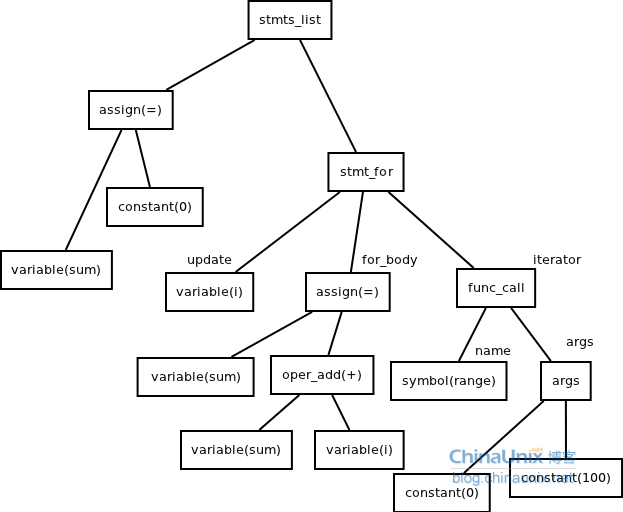
(三)为什么需要抽象语法树

当在源程序语法分析工作时，是在相应程序设计语言的语法规则指导下进行的。语法规则描述了该语言的各种语法成分的组成结构，通常可以用所谓的前后文无关文法或与之等价的Backus-Naur范式(BNF)将一个程序设计语言的语法规则确切的描述出来。前后文无关文法有分为这么几类：LL(1)，LR(0)，LR(1)， LR(k) ,LALR(1)等。每一种文法都有不同的要求，如LL(1)要求文法无二义性和不存在左递归。当把一个文法改为LL(1)文法时，需要引入一些隔外的文法符号与产生式。

例如，四则运算表达式的文法为：

文法1.1

1. E->T|EAT
2. T->F|TMF
3. F->(E)|i
4. A->+|-
5. M->*|/

改为LL(1)后为：

文法1.2

1. E->TE'
2. E'->ATE'|e_symbol
3. T->FT'
4. T'->MFT'|e_symbol
5. F->(E)|i
6. A->+|-
7. M->*|/

例如，当在开发语言时，可能在开始的时候，选择LL(1)文法来描述语言的语法规则，编译器前端生成LL(1)语法树，编译器后端对LL(1)语法树进行处理，生成字节码或者是汇编代码。但是随着工程的开发，在语言中加入了更多的特性，用LL(1)文法描述时，感觉限制很大，并且编写文法时很吃力，所以这个时候决定采用LR(1)文法来描述语言的语法规则，把编译器前端改生成LR(1)语法树，但在这个时候，你会发现很糟糕，因为以前编译器后端是对LL(1)语树进行处理，不得不同时也修改后端的代码。

抽象语法树的第一个特点为:不依赖于具体的文法。无论是LL(1)文法，还是LR(1)，或者还是其它的方法，都要求在语法分析时候，构造出相同的语法树，这样可以给编译器后端提供了清晰，统一的接口。即使是前端采用了不同的文法，都只需要改变前端代码，而不用连累到后端。即减少了工作量，也提高的编译器的可维护性。

抽象语法树的第二个特点为:不依赖于语言的细节。在编译器家族中，大名鼎鼎的gcc算得上是一个老大哥了，它可以编译多种语言，例如c，c＋＋，Java，ADA，Object C， FORTRAN， PASCAL， COBOL等等。在前端gcc对不同的语言进行词法，语法分析和语义分析后，产生抽象语法树形成中间代码作为输出，供后端处理。要做到这一点，就必须在构造语法树时，不依赖于语言的细节，例如在不同的语言中，类似于if－condition－then这样的语句有不同的表示方法

在c中为：

1. if(condition)
2. {
3. do_something();
4. }

在fortran中为：

1. If condition then
2. do_somthing()
3. end if