简易机器学习笔记（八）关于经典的图像分类问题-常见经典神经网络LeNet

前言

图像分类是根据图像的语义信息对不同类别图像进行区分，是计算机视觉的核心，是物体检测、图像分割、物体跟踪、行为分析、人脸识别等其他高层次视觉任务的基础。图像分类在许多领域都有着广泛的应用，如：安防领域的人脸识别和智能视频分析等，交通领域的交通场景识别，互联网领域基于内容的图像检索和相册自动归类，医学领域的图像识别等。

这里简单讲讲LeNet

我的推荐是可以看看这个视频，可视化的查看卷积神经网络是如何一层一层地抽稀获得特征，最后将所有的图像展开成一个一维的轴，再通过全连接神经网络预测得到一个最后的预测值。

手写数字识别 1.4 LeNet-5-哔哩哔哩

计算过程

前置知识：

1. 步长 Stride & 加边 Padding

卷积后尺寸=（输入尺寸-卷积核大小+加边像素数）/步长 + 1

默认Padding = 'valid' (丢弃)，strides = 1

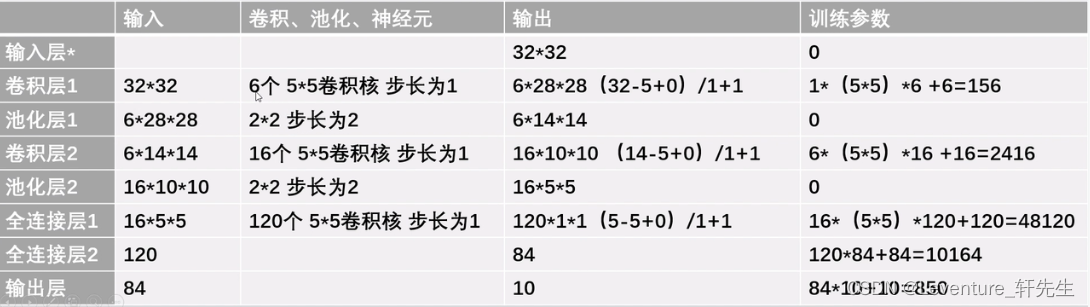
正式计算

1. 卷积层1：

第一层我们给定的图像时32 * 32，使用六个5 x 5的卷积核，步长为1

第一层中没有加边，那么卷积后的尺寸就是（32 - 5 + 0 ）/1 + 1 =28，那么输出的图像就是 28*28的边长

在第一层中，由于我们使用了六个卷积核，我们得到的输出为:62828，可以理解为一个六层厚的图像

1. 池化层1：

我们在池化层内在2x2的图像内选取了一个最大值或者平均值，也就是图片整体缩水到原先的二分之一，所以我们得到池化层的输出为 6 x 14 x 14

1. 卷积层2：

还是按照公式，卷积后尺寸=（输入-卷积核+加边像素数）/步长 + 1，这个时候输入为6 x 14 x 14，这一次我们给定了16个卷积核，得到输出后的尺寸为(14 - 5 + 0)/1 + 1 = 10，得到输出为161010

关于这个16个卷积核是怎么来的，可以见图：

问了下组里的大佬，大佬说这个卷积核数目和层数很多是经验值，即你寻求更多或者更少的卷积核数目或者层数，实际效果不一定有经验值更好，反正都是离散值，就随便试试就行了。

其中：卷积输出尺寸nout：nin为输入原图尺寸大小；s是步长(一次移动几个像素)；p补零圈数，

我们这里输入的值

1. 池化层2

得到 输出后尺寸为16 * 5 * 5

1. 全连接层1：

输入为16 * 5 * 5 ，有120个5*5卷积核，步长为1，输出尺寸为(5 - 5 + 0)/1 + 1 =1,这时候输出的就是一条直线的一维输出了

1. 全连接层2：

输入为120，使用了84个神经元，

1. 输出层

输入84，输出为10

比如我们如图所示，在代码中是这样的：

# 导入需要的包
import paddle
import numpy as np
from paddle.nn import Conv2D, MaxPool2D, Linear

## 组网
import paddle.nn.functional as F
from paddle.vision.transforms import ToTensor
from paddle.vision.datasets import MNIST
#定义LeNet网络结构

# 定义 LeNet 网络结构
class LeNet(paddle.nn.Layer):
    def __init__(self, num_classes=1):
        super(LeNet,self).__init__()
        #创建卷积层和池化层
        #创建第一个卷积层
        self.conv1 = Conv2D(in_channels=1,out_channels=6,kernel_size=5)
        self.max_pool1 = MaxPool2D(kernel_size=2,stride=2)
        #尺寸的逻辑：池化层未改变通道数，当前通道为6
        #创建第二个卷积层
        self.conv2 = Conv2D(in_channels=6,out_channels=16,kernel_size=5)
        self.max_pool2 = MaxPool2D(kernel_size=2,stride=2)
        #创建第三个卷积层
        self.conv3 = Conv2D(in_channels=16,out_channels=120,kernel_size=4)
        # 尺寸的逻辑：输入层将数据拉平[B,C,H,W] -> [B,C*H*W]
        # 输入size是[28,28]，经过三次卷积和两次池化之后，C*H*W等于120
        self.fc1 = Linear(in_features=120, out_features=64)
        # 创建全连接层，第一个全连接层的输出神经元个数为64， 第二个全连接层输出神经元个数为分类标签的类别数
        self.fc2 = Linear(in_features=64, out_features=num_classes)

    # 网络的前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        # 每个卷积层使用Sigmoid激活函数，后面跟着一个2x2的池化
        x = F.sigmoid(x)
        x = self.max_pool1(x)
        x = F.sigmoid(x)
        x = self.conv2(x)
        x = self.max_pool2(x)
        x = self.conv3(x)
        # 尺寸的逻辑：输入层将数据拉平[B,C,H,W] -> [B,C*H*W]
        x = paddle.reshape(x, [x.shape[0], -1])
        x = self.fc1(x)
        x = F.sigmoid(x)
        x = self.fc2(x)
        return x
# 飞桨会根据实际图像数据的尺寸和卷积核参数自动推断中间层数据的W和H等，只需要用户表达通道数即可。
# 下面的程序使用随机数作为输入，查看经过LeNet-5的每一层作用之后，输出数据的形状。

# 输入数据形状是 [N, 1, H, W]
# 这里用np.random创建一个随机数组作为输入数据
x = np.random.randn(*[3,1,28,28])
x = x.astype('float32')

# 创建LeNet类的实例，指定模型名称和分类的类别数目
model = LeNet(num_classes=10)

# 通过调用LeNet从基类继承的sublayers()函数，
# 查看LeNet中所包含的子层
print(model.sublayers())
x = paddle.to_tensor(x)

for item in model.sublayers():
    #item是LeNet类中的一个子层
    #查看经过子层之后的输出数据形状
    try:
        x = item(x)
    except:
        x = paddle.reshape(x, [x.shape[0], -1])
        x = item(x)
    if len(item.parameters())==2:
        # 查看卷积和全连接层的数据和参数的形状，
        # 其中item.parameters()[0]是权重参数w，item.parameters()[1]是偏置参数b
        print(item.full_name(), x.shape, item.parameters()[0].shape, item.parameters()[1].shape)
    else:
        # 池化层没有参数
        print(item.full_name(), x.shape)

# 设置迭代轮数
EPOCH_NUM = 5
#定义训练过程
def train(model,opt,train_loader,valid_loader):
    print("start training ... ")
    model.train()
    for epoch in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            img = data[0]
            label = data[1]
            #计算模型输出
            # 计算模型输出
            logits = model(img)
            # 计算损失函数
            loss_func = paddle.nn.CrossEntropyLoss(reduction='none')
            loss = loss_func(logits, label)
            avg_loss = paddle.mean(loss)

            if batch_id % 2000 == 0:
                print("epoch: {}, batch_id: {}, loss is: {:.4f}".format(epoch, batch_id, float(avg_loss.numpy())))

            #反向传播
            avg_loss.backward()
            opt.step()
            opt.clear_grad()

        model.eval()
        accuracies = []
        losses = []

        for batch_id, data in enumerate(valid_loader()):
            img = data[0]
            label = data[1]
            # 计算模型输出
            logits = model(img)
            pred = F.softmax(logits)

            # 计算损失函数
            loss_func = paddle.nn.CrossEntropyLoss(reduction='none')
            loss = loss_func(logits, label)
            acc = paddle.metric.accuracy(pred, label)
            accuracies.append(acc.numpy())
            losses.append(loss.numpy())
        print("[validation] accuracy/loss: {:.4f}/{:.4f}".format(np.mean(accuracies), np.mean(losses)))
        model.train()
    # 保存模型参数
    paddle.save(model.state_dict(), 'mnist.pdparams')    

# 创建模型
model = LeNet(num_classes=10)
# 设置迭代轮数
EPOCH_NUM = 5
# 设置优化器为Momentum，学习率为0.001
opt = paddle.optimizer.Momentum(learning_rate=0.001, momentum=0.9, parameters=model.parameters())
# 定义数据读取器
train_loader = paddle.io.DataLoader(MNIST(mode='train', transform=ToTensor()), batch_size=10, shuffle=True)
valid_loader = paddle.io.DataLoader(MNIST(mode='test', transform=ToTensor()), batch_size=10)
# 启动训练过程
train(model, opt, train_loader, valid_loader)