Longley数据集——强共线性的宏观经济数据,包含GNP deflator(GNP平减指数)、GNP(国民生产总值)、Unemployed(失业率)、ArmedForces(武装力量)、Population(人口)、year(年份)，Emlpoyed(就业率)。LongLey数据集因存在严重的多重共线性问题，在早期经常用来检验各种算法或计算机的计算精度

Longley数据集来自J．W．Longley（1967）发表在JASA上的一篇论文，是强共线性的宏观经济数据,包含GNP deflator(GNP平减指数)、GNP(国民生产总值)、Unemployed(失业率)、ArmedForces(武装力量)、Population(人口)、year(年份)，Emlpoyed(就业率)。LongLey数据集因存在严重的多重共线性问题，在早期经常用来检验各种算法或计算机的计算精度。

论文：

Longley, J. W. (1967).

An Appraisal of Least Squares Programs for the Electronic Computer from the Viewpoint of the User.

Journal of the American Statistical Association, 62, pp. 819-841.

数据地址：

https://github.com/vincentarelbundock/Rdatasets/blob/master/csv/datasets/longley.csv

-------------------------------------------------------------

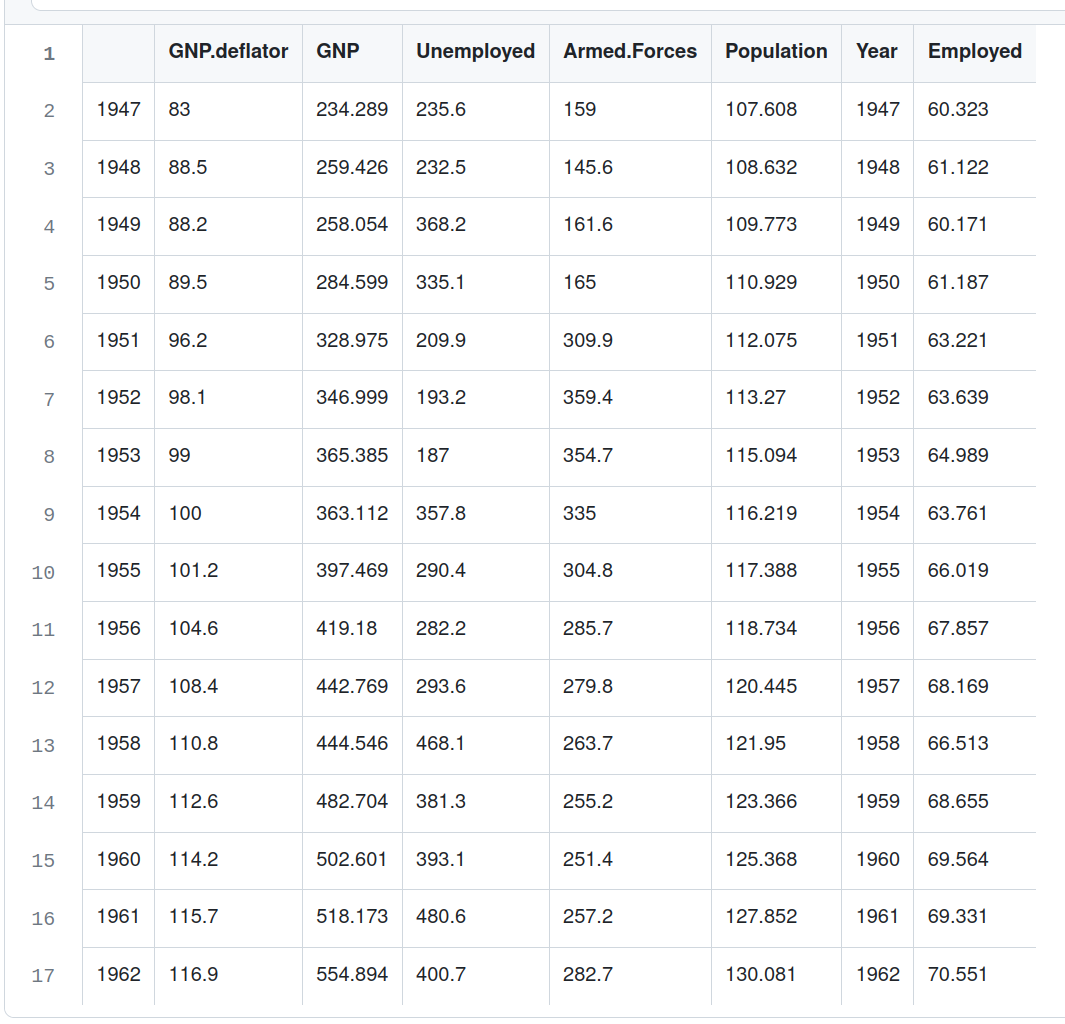
"","GNP.deflator","GNP","Unemployed","Armed.Forces","Population","Year","Employed"
"1947",83,234.289,235.6,159,107.608,1947,60.323
"1948",88.5,259.426,232.5,145.6,108.632,1948,61.122
"1949",88.2,258.054,368.2,161.6,109.773,1949,60.171
"1950",89.5,284.599,335.1,165,110.929,1950,61.187
"1951",96.2,328.975,209.9,309.9,112.075,1951,63.221
"1952",98.1,346.999,193.2,359.4,113.27,1952,63.639
"1953",99,365.385,187,354.7,115.094,1953,64.989
"1954",100,363.112,357.8,335,116.219,1954,63.761
"1955",101.2,397.469,290.4,304.8,117.388,1955,66.019
"1956",104.6,419.18,282.2,285.7,118.734,1956,67.857
"1957",108.4,442.769,293.6,279.8,120.445,1957,68.169
"1958",110.8,444.546,468.1,263.7,121.95,1958,66.513
"1959",112.6,482.704,381.3,255.2,123.366,1959,68.655
"1960",114.2,502.601,393.1,251.4,125.368,1960,69.564
"1961",115.7,518.173,480.6,257.2,127.852,1961,69.331
"1962",116.9,554.894,400.7,282.7,130.081,1962,70.551

--------------------------------------------------------------