Treap，Splay & LCT 学习笔记

从二叉搜索树到平衡树

二叉搜索树（Binary Search Tree）是一种二叉树的树形数据结构，它维护一个集合，并保证它的中序遍历按照递增顺序给出了这个集合的所有元素。由此，可以完成插入，删除，查找元素，查询排名等操作：按照定义确定递归左子树或右子树即可。

可以看出 BST 的时间复杂度与树高相关，那么最优情况下可以达到单次操作 \(O(\log n)\)。但是 BST 很容易退化，最坏情况下会直接退化为链表。于是定义了 BST 的平衡。通常来说，“平衡”会定义为每个结点的左子树和右子树高度差不超过 \(1\)。但实际上在算法竞赛中，只要单次操作均摊 \(O(\log n)\)，就可以称作平衡树了。

对不满足平衡条件的 BST 进行调整，可以使它重新具有平衡性。基本的调整操作是旋转，又分为左旋和右旋。如图所示（图源 OI-wiki），对于结点 \(A\) 的右旋操作是指：将 \(A\) 的左孩子 \(B\) 向右上旋转，代替 \(A\) 成为根节点，将 \(A\) 结点向右下旋转成为 \(B\) 的右子树的根结点，\(B\) 的原来的右子树变为 \(A\) 的左子树。左旋类似。

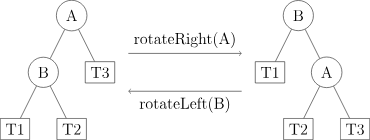
一句话概括，左旋是让右儿子变成根结点，右旋是让左儿子变成根结点。

接下来介绍两种平衡树：Treap 和 Splay。其中 Treap 又可以分为有旋和无旋。

Treap

Treap=Tree+Heap。

顾名思义，Treap 是一棵满足堆性质的 BST。很显然这两个性质是矛盾的，这里的堆性质实际上是给每个元素额外赋予的一个值 priority。这个值是随机给出的。感性理解，这样随机化之后树高就是期望 \(O(\log n)\) 的。

旋转Treap

我们知道旋转是不改变 BST 性质的，所以用旋转维护堆性质就可以了。下面来具体考察一下每个操作。

• 插入：插入一个点之后，如果当前位置不满足堆性质，就要不断往上旋转。
• 删除：先找到这个点，如果这个点不是叶子，就先用旋转把它变成叶子结点，然后删掉。旋转过程中选择左右儿子中更大的一个转到根（假如是大根堆）。
• 查询排名，第 \(k\) 大，前驱，后继等操作不影响 BST 的结构，不需要额外说明。

注意实现的时候并不记录父亲结点，所以要区分左旋和右旋。模板题代码。

#include<bits/stdc++.h>
using namespace std;
mt19937 rnd(time(0));
const int N=1e5+10,INF=1<<30;
int Rand(int l=1,int r=(1<<29)){return rnd()%(r-l+1)+l;}
int rt,val[N],cnt[N],sz[N],ls[N],rs[N],pri[N],tot;
int node(int v){val[++tot]=v;pri[tot]=Rand();sz[tot]=cnt[tot]=1;return tot;}
void push_up(int p){sz[p]=cnt[p]+sz[ls[p]]+sz[rs[p]];}
void zig(int&p){int q=ls[p];ls[p]=rs[q];rs[q]=p;push_up(p);push_up(q);p=q;}
void zag(int&p){int q=rs[p];rs[p]=ls[q];ls[q]=p;push_up(p);push_up(q);p=q;}
void init(){rt=node(-INF);rs[rt]=node(INF);push_up(rt);}
void ins(int&p,int x){
    if(!p){p=node(x);return;}
    if(x==val[p])++cnt[p];
    else if(x<val[p]){ins(ls[p],x);if(pri[p]<pri[ls[p]])zig(p);}
    else {ins(rs[p],x);if(pri[p]<pri[rs[p]])zag(p);}
    push_up(p);
}
void del(int&p,int x){
    if(!p)return;
    if(x==val[p]){
        if(cnt[p]>1){--cnt[p];push_up(p);return;}
        if(ls[p]||rs[p]){
            if(!rs[p]||pri[ls[p]]>pri[rs[p]])zig(p),del(rs[p],x);
            else zag(p),del(ls[p],x); push_up(p);
        }else p=0; return;
    }
    if(x<val[p])del(ls[p],x);else del(rs[p],x);
    push_up(p);
}
int rnk(int p,int x){
    if(!p)return 1;
    if(x==val[p])return sz[ls[p]]+1;
    else if(x<val[p])return rnk(ls[p],x);
    else return sz[ls[p]]+cnt[p]+rnk(rs[p],x);
}
int kth(int p,int k){
    if(!p)return INF;
    if(k<=sz[ls[p]])return kth(ls[p],k);
    else if(k<=sz[ls[p]]+cnt[p])return val[p];
    else return kth(rs[p],k-sz[ls[p]]-cnt[p]);
}
int prev(int x){
    int p=rt,pre=-INF;
    while(p){
        if(val[p]<x)pre=val[p],p=rs[p];
        else p=ls[p];
    }
    return pre;
}
int next(int x){
    int p=rt,nxt=INF;
    while(p){
        if(val[p]>x)nxt=val[p],p=ls[p];
        else p=rs[p];
    }
    return nxt;
}
int main(){
    init();int q;scanf("%d",&q);
    while(q--){
        int op,x;scanf("%d%d",&op,&x);
        if(op==1)ins(rt,x);
        if(op==2)del(rt,x);
        if(op==3)printf("%d\n",rnk(rt,x)-1);
        if(op==4)printf("%d\n",kth(rt,x+1));
        if(op==5)printf("%d\n",prev(x));
        if(op==6)printf("%d\n",next(x));
    }
    return 0;
}

无旋Treap

无旋Treap，又称 Fhq-Treap，顾名思义就是不用旋转来满足堆性质的平衡树。它的两种基本操作是分裂与合并。

分裂（Split）是指将一棵 Treap 按照中序遍历的顺序分割成左右两半，满足两半组成的 Treap 所有值都不变。它需要一个参数 \(k\)，表示把中序遍历的前 \(k\) 个结点分离出来。具体实现很容易，要么一个子树的左子树和根都在第一棵树内，要么一个子树的右子树和根都在第二棵树内，于是递归下去就可以了。

合并（Merge）是将两棵（由原先的 Treap Split 得到的）Treap 合并在一起，按照中序遍历的顺序，并且所有结点的值都不变。注意第一棵树的所有数小于第二棵树的所有数。合并操作先比较两棵树的根的 pri 值决定以那个点为根，然后递归到子树内即可。

听起来很玄学，那么具体看看各种操作怎么实现。

• 查询排名和原来是一样的。
• 插入 \(x\)，先查询 \(x\) 的排名 \(k\)，然后按照 \(k\) 做一次 Split，把 \(x\) 看作一个新结点，做两次 Merge。
• 删除 \(x\)，先查询 \(x\) 的排名 \(k\)，然后按照 \(k-1,k\) 做两次 Split，丢掉中间那个点，把剩下两个树 Merge 起来。
• 查询第 \(k\) 大，按照 \(k-1,k\) 做两次 Split，然后中间那个就是需要的答案。
• 前驱就是 kth(rnk(val-1))。后继就是 kth(rnk(val+1))。

无旋 Treap 相较于带旋 Treap 的优势，除了常数和（可能）好写之外，更重要的是它的可拓展性。比如说，无旋 Treap 可以方便地支持区间操作：Split 操作得到的就是一个个区间。那么进一步，还可以像线段树一样打区间标记和懒惰标记，等等。

模板题代码。给每个结点记录一个翻转标记。

#include<bits/stdc++.h>
using namespace std;
mt19937 rnd(time(0));
int Rand(int l=1,int r=(1<<29)){return rnd()%(r-l+1)+l;}
const int N=1e5+5;
int n,m;
int rt,val[N],sz[N],pri[N],ls[N],rs[N],tag[N],tot;
int node(int v){val[++tot]=v;sz[tot]=1;pri[tot]=Rand();return tot;}
void push_up(int p){sz[p]=sz[ls[p]]+sz[rs[p]]+1;}
void push_down(int p){
    if(!tag[p])return;tag[p]=0;
    tag[ls[p]]^=1;tag[rs[p]]^=1;swap(ls[p],rs[p]);
}
void split(int p,int k,int&u,int&v){
    if(!p){u=v=0;return;} push_down(p);
    if(k<=sz[ls[p]])v=p,split(ls[p],k,u,ls[p]);
    //如果分点在左子树中，那么把当前结点作为第二个子树的根
    //递归下去，两棵子树分别是第一个子树和当前结点的左儿子
    else u=p,split(rs[p],k-sz[ls[p]]-1,rs[p],v);
    push_up(p);
}
int merge(int p,int q){
    if(!p||!q)return p^q;
    if(pri[p]>pri[q]){//比较优先级
        push_down(p);rs[p]=merge(rs[p],q);
        push_up(p);return p;
    }
    else{
        push_down(q);ls[q]=merge(p,ls[q]);
        push_up(q);return q;
    }
}
void print(int p){
    if(!p)return;push_down(p);
    print(ls[p]),printf("%d ",val[p]),print(rs[p]);
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)node(i),rt=merge(rt,tot);
    for(int i=1,l,r;i<=m;i++){
        scanf("%d%d",&l,&r);int u,mid,v;
        split(rt,r,u,v);split(u,l-1,u,mid);
        tag[mid]^=1;rt=merge(merge(u,mid),v);
    }
    print(rt);
    return 0;
}

除了按照排名 Split，按照权值 Split 也是可以的。后者一般用在数字会有重复的情形下。但很多时候我们使用 Fhq-Treap 是为了按照顺序维护一个序列，所以并不常用。

Splay

Splay 树是一种均摊的平衡树，它也是用旋转来维持平衡的。这里和 Treap 的旋转可能略有区别，旋转是放在子结点上的，对左儿子的旋转叫右旋，对右儿子的旋转叫左旋。

Splay 树的独有操作是伸展（splay），即把一个点通过旋转变成根结点。一个直接的做法就是每一次都对目标结点旋转，这种做法称为单旋。然而单旋的复杂度是错误的，我们需要使用双旋。也就是说，我们额外判断一下当前结点的父结点是否同为左儿子（或同为右儿子），如果是，就先旋转父结点，再旋转子结点。

要维持平衡，只需要在每一次操作之后，都对最终访问的结点做 splay 操作。以 \(\sum \log(sz(x))\) 为势能函数分析可以得到复杂度。因此 splay 的实现并没有什么特殊的地方。

模板题代码。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,INF=1e9;
int n;
struct Splay{
	int rt,tot,fa[N],ch[N][2],val[N],cnt[N],siz[N];
	void push_up(int p){siz[p]=siz[ch[p][0]]+siz[ch[p][1]]+cnt[p];}
	bool get(int p){return p==ch[fa[p]][1];}
	void clear(int p){fa[p]=ch[p][0]=ch[p][1]=val[p]=cnt[p]=siz[p]=0;}
	void rotate(int x){
		int y=fa[x],z=fa[y],op=1-get(x);
		ch[y][op^1]=ch[x][op];if(ch[x][op])fa[ch[x][op]]=y;
		ch[x][op]=y;fa[y]=x;fa[x]=z;if(z)ch[z][y==ch[z][1]]=x;
		push_up(y);push_up(x);
	}
	void splay(int x,int goal=0){
		for(int p=fa[x];p!=goal;p=fa[x]){
			if(fa[p]!=goal)rotate(get(p)==get(x)?p:x);
			rotate(x);
		}if(!goal)rt=x;
	}
	void ins(int v){
		if(!tot){rt=tot=1;val[1]=v;cnt[1]=siz[1]=1;return;}
		int p=rt,f=0;
		while(1){
			if(val[p]==v){++cnt[p];++siz[p];push_up(f);splay(p);break;}
			f=p;p=ch[p][val[p]<v];
			if(!p){
				val[p=++tot]=v;cnt[p]=siz[p]=1;
				fa[tot]=f;ch[f][val[f]<v]=p;
				push_up(f);splay(p);break;
			}
		}
	}
	bool find(int v){
		int p=rt;
		while(p){
			if(val[p]==v){splay(p);return true;}
			p=ch[p][val[p]<v];
		}return false;
	}
	void merge(int x,int y){
		while(ch[x][1])x=ch[x][1];
		splay(x);ch[x][1]=y;fa[y]=x;push_up(x);
	}
	void del(int v){
		if(!find(v))return;
		if(cnt[rt]>1){--cnt[rt],--siz[rt];return;}
		int x=ch[rt][0],y=ch[rt][1];
		fa[x]=fa[y]=0;clear(rt);
		if(!x||!y){rt=x+y;return;}
		merge(x,y);
	}
	int rank(int v){
		find(v);
		return siz[ch[rt][0]]+1;
	}
	int kth(int k){
		int p=rt;
		while(1){
			if(ch[p][0]&&k<=siz[ch[p][0]])p=ch[p][0];
			else{
				k-=cnt[p]+siz[ch[p][0]];
				if(k<=0){splay(p);return val[p];}
				p=ch[p][1];
			}
		}
	}
	int nxt(int x,int op){
		ins(x);int p=ch[rt][op^1];
		if(!p)return -1;
		while(ch[p][op])p=ch[p][op];
		int res=val[p];del(x);
		return res;
	}
}cst;
int main(){
	scanf("%d",&n);
	cst.ins(INF);cst.ins(-INF);
	for(int i=1,op,x;i<=n;i++){
		scanf("%d%d",&op,&x);
		if(op==1)cst.ins(x);
		if(op==2)cst.del(x);
		if(op==3)printf("%d\n",cst.rank(x)-1);
		if(op==4)printf("%d\n",cst.kth(x+1));
		if(op==5)printf("%d\n",cst.nxt(x,1));
		if(op==6)printf("%d\n",cst.nxt(x,0));
	}
	return 0;
}

Splay 和 Fhq-Treap 一样可以进行区间操作。具体来说，在 splay 的时候，我们不一定会将一个结点旋转到根，而是可以旋转到某个结点的儿子。这时，我们注意到在维护序列时，Splay 的一棵子树就代表一个区间，因此要提取区间 \([l,r]\)，只要先将 \(l-1\) splay 到根，再将 \(r+1\) splay 到根的右儿子，需要的子树就是 \(r+1\) 的左儿子。

模板题代码。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m,ans[N],cnt;
struct Splay{
	int rt,tot,fa[N],ch[N][2],val[N],tag[N],siz[N];
	void push_up(int p){siz[p]=siz[ch[p][0]]+siz[ch[p][1]]+1;}
	int build(int l,int r){
		if(l==r){push_up(l);return l;}
		int p=l+r>>1;
		if(l<p)fa[ch[p][0]=build(l,p-1)]=p;
		if(p<r)fa[ch[p][1]=build(p+1,r)]=p;
		push_up(p);
		return p;
	}
	bool get(int p){return p==ch[fa[p]][1];}
	void push_down(int p){
		if(!tag[p])return;
		tag[ch[p][0]]^=1;tag[ch[p][1]]^=1;
		tag[p]=0;swap(ch[p][0],ch[p][1]);
	}
	void rotate(int x){
		int y=fa[x],z=fa[y],op=get(x)^1;
		ch[y][op^1]=ch[x][op];if(ch[x][op])fa[ch[x][op]]=y;
		ch[x][op]=y;fa[y]=x;fa[x]=z;if(z)ch[z][y==ch[z][1]]=x;
		push_up(y);push_up(x);
	}
	void splay(int x,int goal){
		for(int p=fa[x];p!=goal;p=fa[x]){
			if(fa[p]!=goal)rotate(get(p)==get(x)?p:x);
			rotate(x);
		}if(!goal)rt=x;
	}
	int kth(int k){
		int p=rt;
		while(1){
			push_down(p);
			if(ch[p][0]&&k<=siz[ch[p][0]])p=ch[p][0];
			else{
				k-=siz[ch[p][0]]+1;
				if(k<=0)return p;
				p=ch[p][1];
			}
		}
	}
	void update(int l,int r){
		l=kth(l-1);splay(l,0);
		r=kth(r+1);splay(r,l);
		tag[ch[r][0]]^=1;
	}
	void dfs(int p){
		push_down(p);
		if(ch[p][0])dfs(ch[p][0]);
		if(p!=1&&p!=n+2)printf("%d ",p-1);
		if(ch[p][1])dfs(ch[p][1]);
	}
}cst;
int main(){
	scanf("%d%d",&n,&m);
	cst.rt=cst.build(1,n+2);
	for(int i=1,l,r;i<=m;i++){
		scanf("%d%d",&l,&r);
		cst.update(l+1,r+1);
	}
	cst.dfs(cst.rt);
	return 0;
}

LCT

写了两天平衡树突然不想写了。会补吗？会补的。