卷积神经网络（Convolutional Neural Network,CNN）思想 实例 具体代码实现

　　在前面我们讨论了神经网络初步，学习了神经网络中最基础的部分：全连接层，并且实现了搭建两层全连接实现图片分类的问题，达到了50%左右的正确率，全连接层的主要思想是构建出一个映射函数，使得前一层的所有输入，都对于该层的输出产生相应的贡献，换句话说，是前一层的所有输入都参与到我们神经元的映射函数中进行计算，最终得到具体的分数向量或是对下一层新的输入。在全连接层之间，我们引入了非线性的激活函数进行约束，使最终的结果能够实现非线性的功能，一共有若干种激活函数，例如ReLU，Leaky ReLU，Tanh，Sigmoid等等，其用途和具体的作用参见https://www.cnblogs.com/Lbmttw/p/16858127.html这篇博客，相对而言说的比较明白。

　　今天在这里我们需要讨论的是卷积神经网络（Convolutional Neural Network）也是在各方面具有极高的用途的一个深度学习的框架。值得注意的是，在2012年，一举拿下ImageNet图像分类的桂冠的方法是AlexNet，其思想内核就是CNN！也自从CNN加入到具体的分类任务中之后，我们对于图片分类问题的准确率变得越来越高。

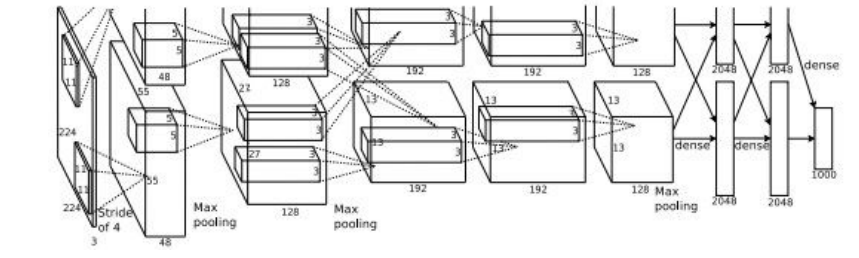
　　（该图为AlexNet的具体模型图）

　　CNN之所以起名叫做卷积神经网络，是因为其神经网络结构中带有卷积层；在数学中两个函数的卷积，本质上是先将一个函数翻转，然后不断的滑动并叠加。在我们卷积神经网络中，也是同样的操作。卷积层通过卷积核不断的在输入的数据上滑动，并且计算当前位置的权重值，最后进行叠加。在具体介绍卷积层之前，我们先来说一下卷积神经网络具体都由哪些结构构成：输入---卷积---激活函数---池化---卷积....---全连接---...---最终输出层。我们神经网络中的卷积，与全连接层一样，可以进行多次操作，但是需要注意的是，我们每次操作过后，都需要加一个激活函数或者叫非线性层，这个与前篇博客我们所述的神经网络计算模型高度与人体神经元仿真是相一致的。

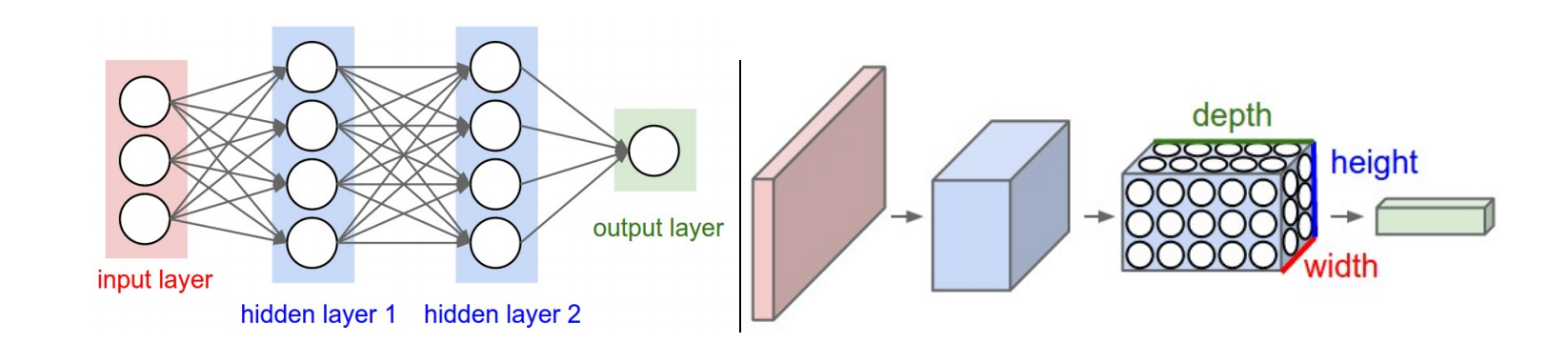
　　我们先从输入层介绍：输入是一幅图像，我们经过处理后得到的是一个n*n*3的numpy数组，其中n是该图片的分辨率，也就是像素点的个数。在全连接层中，我们将这个三维的numpy数组转化为了二维的numpy数组，这么做显然可以方便我们后续的映射过程，但是相应的，破坏了原本numpy数组中每个像素点的相对位置，将三维的numpy数组硬生生reshape或者stretch成一个二维的数组，显然破坏了原本的结构，这对于我们提取图像的特征显然是不利的。而我们卷积层对于输入的数据就没有这步操作，保持了原本的空间结构的稳定性，显然，在这里，就要明显优于全连接神经网络了。

　　然后是卷积层，在上面我们也讨论过，卷积层中的卷积定义与数学上的卷积极为相似，通过卷积核不断的在输入的数据上滑动，每次计算出相应位置的权重并叠加。卷积层的参数由一组可学习的卷积核（Filter）组成，每一个这种Filter在空间上的尺寸都很小，但是它必须要在深度上与输入数据保证同型，例如原本的数据规模为32*32*3，其中3为RGB颜色空间的通道数，那么我们的Filter的尺寸就必须为n*m*3，n和m可以由我们指定，但是第三维度必须为3。在我们Filter不断的在输入数据上滑动的过程中，我们需要计算对应位置的点积，最终则会产生一个二维的激活图；在这个图中，每个位置对应的数字可以看做Filter在对应位置的相应，或者换句话说，卷积层在不断的提取对应位置的特征。当然，需要注意的一点是，我们卷积层中可以有很多个独立的Filter，这些Filter都具有独立的参数，或者换句话说有着独立的映射关系，每一个Filter所产生的二维激活图将会在深度方向不断叠加产生最终的输出层，也就是输出层的深度（第三维度）就是Filter的数量。

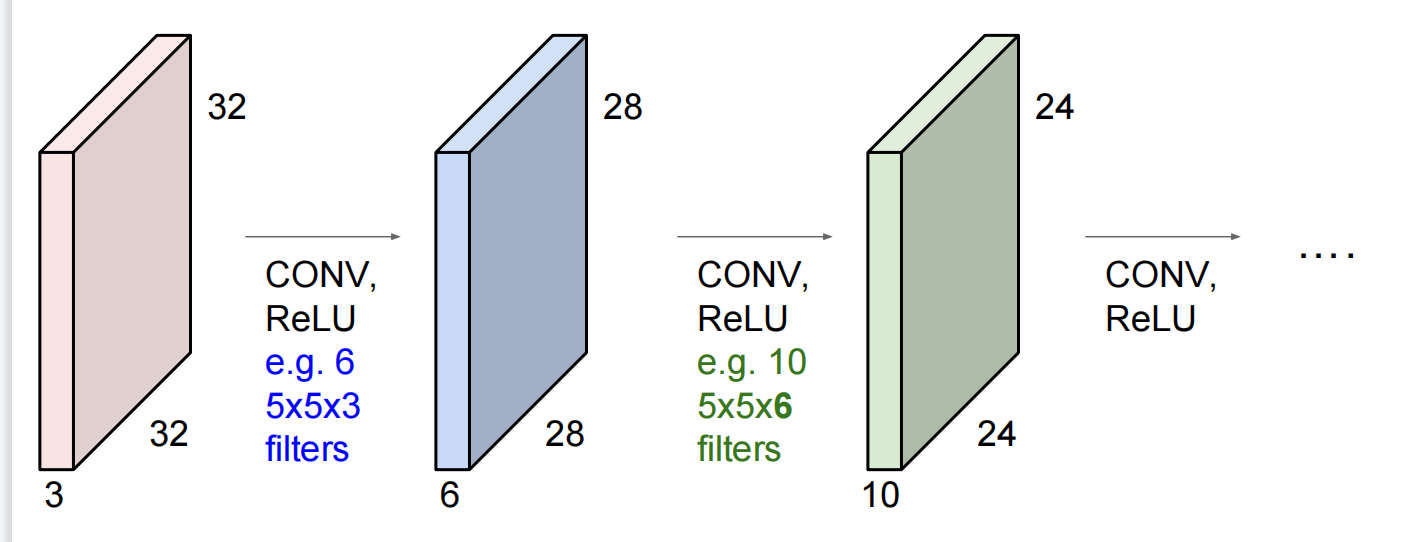
　　下面我们来考虑一下池化层，卷积神经网络重要的层级之一，池化层（Pooling）所起到的主要作用是对输入样本进行downsamping，起到减少参数，缩小数据规模，防止过拟合。池化层同样也需要有相应尺寸大小的Filter，尺寸大小可以由我们自由指定；我们最常用的池化Filter是2×2的Filter，池化Filter的规模以及每次池化的步长决定了缩小数据规模的程度，例如我们刚才所说2×2的Filter，在步长为2的情况下就可以缩小75%的数据规模；假设原本是4×4×n的输入数据，那么在经过池化层后，就变成了2×2×n的输出数据，显然，这缩小了75%的参数。当然，在每个Filter内部也依旧有对应的映射关系，和卷积层一样，我们的池化层Filter也需要同对应位置的输入数据进行运算，不过不同的是，一般而言池化层的映射关系往往由我们直接指定，而不是通过数据不断的更新迭代。常见的pooling有Max Pooling，Average Pooling等。在这里我们用Max Pooling举例子：

　　如上图所示，在这里，我们是采用了2×2的Filter，步长（stride）为2，并且Filter内部是取最大值的关系，在上图的左侧，体现的是经过池化层之前以及之后的数据规模，在右侧，体现的是max Pooling所做的操作，即在对应位置取最大值。我们从上面的例子不难看出，池化层也是对我们的数据进行局部采样，得到局部的特征。池化层很显然，也有相应的问题，舍弃了部分的数据可能导致我们的模型欠拟合等问题，但是这些都是可以通过训练轮数的增加等解决的问题。

　　【争议】目前对于池化层，很多人不太喜欢这个层级，认为池化层完全可以舍弃，只使用重复的卷积层构成整个卷积神经网络。他们建议偶尔在卷积层中使用更大的stride以完全替代池化层的作用（将在下面代码部分详述卷积层的stride）

　　

　　然后就是全连接层，对于全连接层，前面一层所有的神经元都需要参与到后续的计算中，将所有的数据层数统一归一到一起，形成一个分数矩阵/分数向量，然后便于我们根据分数去进行判断。这个全连接层与前面神经网络初步https://www.cnblogs.com/Lbmttw/p/16858127.html这篇博客中说的很清楚，在这里就不赘述了。

　　以上便是卷积神经网络的一些基本的层次结构，值得注意的是，无论什么神经网络到最后的目的都很简单，就是要将损失最小化，计算loss的目的也即不断优化我们的映射关系，使得我们的神经网络能够更加逼近真实场景/做出最优的判断，在非图像分类任务中，例如图像生成等，可能损失就需要我们重新定义，但是总的来说，神经网络亦或是深度学习的基本思想便是将某个场景建模为可学习的网络结构，通过不断优化我们人为规定的损失使得网络能够更加优秀的执行我们的任务。下面是代码部分；将从几个方面分别去介绍，一个是目前的深度学习框架(keras)，另一个则是完完全全将每一个步骤都实际的写出来。下面则是对于具体代码的分析：

　　首先我们要分析的是卷积层的前向传播，下面是代码实例：

 1 def conv_forward_naive(x, w, b, conv_param):
 2
 3     out = None
 4     ans = None
 5     pad = conv_param['pad']
 6     stride = conv_param['stride']
 7     N, C, H, W = x.shape
 8     F, C, FH, FW = w.shape
 9     assert (H - FH + 2 * pad) % stride == 0
10     assert (W - FW + 2 * pad) % stride == 0
11     outH = 1 + (H - FH + 2 * pad) / stride
12     outW = 1 + (W - FW + 2 * pad) / stride
13     out = np.zeros((N, F, int(outH), int(outW)))
14     x_pad = np.pad(x, ((0,0), (0,0),(pad,pad),(pad,pad)), 'constant')
15     H_pad, W_pad = x_pad.shape[2], x_pad.shape[3]
16     w_row = w.reshape(F, C*FH*FW)
17     x_col = np.zeros((int(C*FH*FW), int(outH*outW)))
18     for index in range(N):
19         neuron = 0
20         for i in range(0, H_pad-FH+1, stride):
21             for j in range(0, W_pad-FW+1,stride):
22                 x_col[:,neuron] = x_pad[index,:,i:i+FH,j:j+FW].reshape(C*FH*FW)
23                 neuron += 1
24         out[index] = (w_row.dot(x_col) + b.reshape(F,1)).reshape(int(F), int(outH), int(outW))
25     cache = (x, w, b, conv_param)
26     return out, cache

conv_forward_naive

　　在上面的代码中，我们实现的是卷积层的前向传播，我们需要输入数据为：

　　　　1.X：输入数据，形状为（N、C、H、W）

　　　　2.W：权重矩阵，也即映射关系，形状为（F、C、HH、WW）

　　　　3.b：偏置项，形状为（F，）

　　　　4.conv_param：具有以下关键字的字典：“stride”：水平和垂直方向每次移动的距离，与池化层中的stride是类似的，也可以称之为步幅；“pad”：用于零填充输入的像素数。在填充过程中，“pad”零应对称放置（即两侧相等）沿着输入的高度和宽度轴。

　　值得注意的是，padding这个操作是这样的：

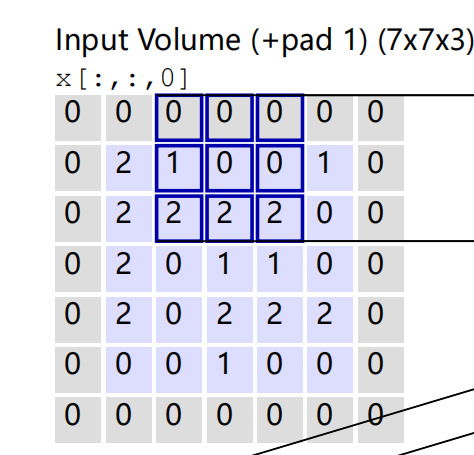
　　原本的数据是紫色区域，我们加了padding=1，使得原本数据周围一圈多了一层0，加padding可以让我们的卷积核能够扫描到边界的信息，如若不加padding，边界四个角只会被扫描一次，这显然会丢失部分信息，所以加上padding项就能够更充分的扫描到数据的边界；此外，padding操作也可以补齐不对齐的数据，由于我们大部分的神经网络的映射都是矩阵运算和点积等，要求参与运算的两个矩阵之间具有一定的规模关系，而加上padding则可以使原本不对齐的数据变得对齐。

　　返回数据为：

　　　　1.out：形状为（N，F，H'，W'）的输出数据，也就是经过映射过后卷积层的输出数据，其中H'和W'由H’=1+（H+2*padding-HH）/stride，W'=1+（W+2*padding-WW）/stride。这个公式很简单，基于卷积操作很容易能写出来，就不详细推导了。

　　　　2.缓存：（x，w，b，conv_param）

　　在介绍完这些过后，我们很轻松就能知道前向传播需要做的事情：首先，对输入的数据进行padding操作，然后利用循环结构不断的遍历整个输入数据，不断的进行卷积，然后将结果存储到out数据中，最后将所有的参数缓存到cache元组中即可。

　　介绍完前向传播，我们来考虑反向传播；由于我们卷积神经网络仍然是神经网路，优化仍然是基于梯度的做的操作，所以我们仍然需要对每一层神经网络都设计出相对应的反向传播算法以便于计算梯度，有关bp算法在前面已经说的比较详细了，在这里就不赘述了https://www.cnblogs.com/Lbmttw/p/16844897.html可以参考这篇博客。我们直接来看代码：　

 1 def conv_backward_naive(dout, cache):
 2     dx, dw, db = None, None, None
 3     x, w, b, conv_param = cache
 4     N, C, H, W = x.shape
 5     F, _, HH, WW = w.shape
 6     stride = conv_param.get('stride', 1)
 7     pad = conv_param.get('pad', 0)
 8     x_pad = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant', constant_values=0)
 9     H_prime = 1 + (H + 2 * pad - HH) // stride
10     W_prime = 1 + (W + 2 * pad - WW) // stride
11     dx_pad = np.zeros_like(x_pad)
12     dx = np.zeros_like(x)
13     dw = np.zeros_like(w)
14     db = np.zeros_like(b)
15     for n in range(N):
16         for f in range(F):
17             db[f] += dout[n, f].sum()
18             for j in range(0, H_prime):
19                 for i in range(0, W_prime):
20                     dw[f] += x_pad[n, :, j * stride:j * stride + HH, i * stride:i * stride + WW] * dout[n, f, j, i]
21                     dx_pad[n, :, j * stride:j * stride + HH, i * stride:i * stride + WW] += w[f] * dout[n, f, j, i]
22     dx = dx_pad[:, :, pad:pad+H, pad:pad+W]
23     return dx, dw, db

conv_backward_naive

　　在这里，与前面全连接层的反向传播一样，仍然需要我们传入上游梯度，以及该层对应的缓存参数进行运算，最后输出的结果是对于x,w,b的梯度；这里的方法与前面全连接层的类似，仍然是计算梯度要针对于每一个卷积核部分单独计算而已。