voj 1754 spfa

最优贸易

最优贸易

描述

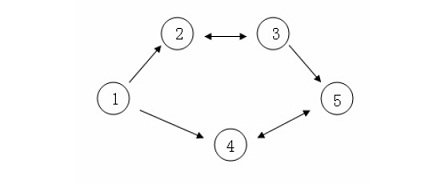
C 国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。任意两个 城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路，一部分 为双向通行的道路，双向通行的道路在统计条数时也计为 1 条。 C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价 格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。 商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息 之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 C 国 n 个城 市的标号从 1~ n，阿龙决定从 1 号城市出发，并最终在 n 号城市结束自己的旅行。在旅游的 过程中，任何城市可以重复经过多次，但不要求经过所有 n 个城市。阿龙通过这样的贸易方 式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品——水晶球，并在之后经过的另 一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游，他决定 这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。 假设 C 国有 5 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路 为单向通行，双向箭头表示这条道路为双向通行。

假设 1~n 号城市的水晶球价格分别为 4，3，5，6，1。 阿龙可以选择如下一条线路：1->2->3->5，并在 2 号城市以 3 的价格买入水晶球，在 3 号城市以 5的价格卖出水晶球，赚取的旅费数为 2。 阿龙也可以选择如下一条线路 1->4->5->4->5，并在第 1 次到达 5 号城市时以 1 的价格 买入水晶球，在第 2 次到达 4 号城市时以 6 的价格卖出水晶球，赚取的旅费数为 5。

现在给出 n个城市的水晶球价格，m条道路的信息（每条道路所连接的两个城市的编号 以及该条道路的通行情况） 。请你告诉阿龙，他最多能赚取多少旅费。

格式

输入格式

第一行包含 2 个正整数 n 和 m，中间用一个空格隔开，分别表示城市的数目和道路的 数目。 第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城 市的商品价格。 接下来 m行， 每行有 3 个正整数， x， y， z， 每两个整数之间用一个空格隔开。 如果 z=1， 表示这条道路是城市 x到城市 y之间的单向道路；如果 z=2，表示这条道路为城市 x 和城市 y之间的双向道路。

输出格式

输出共1 行， 包含 1 个整数， 表示最多能赚取的旅费。 如果没有进行贸易， 则输出 0。

样例1

样例输入1

5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2

样例输出1

5

限制

每个测试点1s

输入数据保证 1 号城市可以到达n 号城市。 对于 10%的数据，1≤n≤6。 对于 30%的数据，1≤n≤100。 对于 50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。 对于 100%的数据，1≤n≤100000，1≤m≤500000，1≤x，y≤n，1≤z≤2，1≤各城市 水晶球价格≤100。

来源

NOIP 2009

首先我们知道一定要先买完之后才能进行卖的操作，假设我们在k点买了水晶球，那么卖点m一定是在某一条k-->N的路径上的某一个点，因为最后的终点是N,反之从N也一定能到达这个卖点m,所以我们有了思路.

我们可以枚举所有点为买点，显然这是从1开始跑一下spfa找到每条路径的最小权值德文操作。

我们找到买点还需要找到最大的卖点，我们发现对于每个买点k，其最大卖点就是从N-->k的路径最大权值，显然也可以反向跑一下spfa!

一开始想跑dij发现不满足低级的贪心需求，所以还是sfpa吧。

#include<bits/stdc++.h>
using namespace std;
#define pb push_back
#define inf 0x3f3f3f3f
int N,M,C[100005];
vector<int> g1[100005],g2[100005];
int d1[100005],d2[100005];
bool vis[100005];
void spfa()
{
    memset(d1,inf,sizeof(d1));
    memset(d2,0,sizeof(d2));
    queue<int> Q;
    Q.push(1);
    vis[1]=1;
    d1[1]=C[1];
    while(!Q.empty()){
        int u=Q.front(); Q.pop();
        vis[u]=0;
        for(int i=0;i<g1[u].size();i++){ int x=g1[u][i];
            if(d1[x]>min(d1[u],C[x])){
                d1[x]=min(d1[u],C[x]);
                if(!vis[x]) { Q.push(x); vis[x]=1;}
            }
        }
    }

memset(vis,0,sizeof(vis));
    while(!Q.empty()) Q.pop();
    Q.push(N);
    vis[N]=1;
    d2[N]=C[N];
    while(!Q.empty()){
      int u=Q.front();  Q.pop();
      vis[u]=0;
      for(int i=0;i<g2[u].size();i++){int x=g2[u][i];
      if(d2[x]<max(d2[u],C[x])){
           d2[x]=max(d2[u],C[x]);
           if(!vis[x]) {Q.push(x); vis[x]=1;}
      }
      }
    }
    int ans=0;  bool pd=false;
for(int i=1;i<=N;++i)
if(d1[i]!=inf&&d2[i]!=0)   {pd=1;ans=max(ans,abs(d1[i]-d2[i]));}
if(!pd) ans=0;
cout<<ans<<endl;
}
int main()
{
    int i,j,k;
    int a,b,c;
    cin>>N>>M;
    for(i=1;i<=N;++i) scanf("%d",&C[i]);
    for(i=1;i<=M;++i){
        scanf("%d%d%d",&a,&b,&c);
        g1[a].pb(b);
        g2[b].pb(a);
        if(c==2){
            g1[b].pb(a);
            g2[a].pb(b);
        }
    }
    spfa();
    return 0;
}