7. B+树

一、B+树是应文件系统所需而产生的一种B树的变形树

1. 定义（使用阶数m来定义）

1. 除了根结点外，其他非终端结点最多有m个关键字，最少有⌈m/2⌉个关键字
2. 结点中的每个关键字对应一个子树
3. 所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字

4. 所有的叶子节点包含了全部的关键字以及指向含有这些关键字记录的指针，并且：

   • 同一叶子节点中的关键字按大小顺序排列
   • 相邻的叶子节点顺序链接（相当于是构成了一个顺序链表）
   • 所有叶子节点在同一层

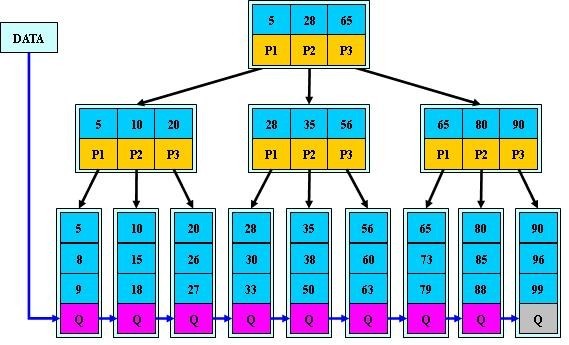
2. 和B树的区别

对于非终端结点，关键字的个数与其子树的个数相同；不像B树，子树的个数总比关键字的个数多1。

所有的关键字及相应的指针都在叶子结点中；不像B树，有的关键字是在内部结点中。（换句话说，在B+树中，内部结点仅仅起到索引的作用。在搜索过程中，如果待查询的关键字和内部结点的关键字一致，那么搜索过程不停止，而是继续向下搜索这个分支）

1. 关键字的数量不同：B+树中，对于非终端结点，关键字的个数与其子树的个数相同；而B树中，关键字的个数比子树的个数少1。
2. 存储的位置不同：B+树中的数据都存储在叶子结点上，也就是其所有叶子结点的数据组合起来就是完整的数据；而B树的数据存储在每一个结点中。
3. 非终端结点的构造不同：B+树的非终端结点仅仅存储着关键字信息和指向孩子的指针（这里的指针指的是磁盘块的偏移量），也就是说内部结点仅仅包含着索引信息。
4. 查询不同：B树在找到具体的数值以后，则结束；而B+树则需要通过索引找到叶子结点中的数据才结束，也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径。

二、关于B+树的面试题

1. 为何B+树用于数据库索引？

B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题。B树的其非终端结点同样存储着数据，因此如果我们要找到具体的数据，就需要进行一次中序遍历。正是为了解决这个问题，B+树应运而生。

B+树的数据都存储在叶子结点中，非终端结点均为索引，方便扫库，只需要遍历叶子结点即可实现整棵树的遍历。所以B+树更加适合在区间查询的情况，而且在数据库中基于范围的查询是非常频繁的，所以通常B+树用于数据库索引。

2. 为何相比于B树，B+树在文件系统和数据库系统中更具优势？

①B+树的磁盘读写代价更低 
B+树的非终端结点并没有指向关键字具体信息的指针，因此其内部结点相对B树更小。如果把同一非终端结点的所有关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说I/O读写次数也就降低了。

举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶B树(一个结点最多8个关键字)的非终端结点需要2个盘快。而B+树非终端结点只需要1个盘快。当需要把非终端结点读入内存中的时候，B树就比B+树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。

②B+树的查询效率更加稳定 
由于非终端结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路径。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

③B+树更有利于对数据库的扫描 
B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题，而B+树只需要遍历叶子节点就可以解决对全部关键字信息的扫描，所以对于数据库中频繁使用的范围查询，B+树有着更高的性能。