《编译原理》画 DAG 图与求优化后的 4 元式代码- 例题解析

DAG 图（Directed Acylic Graph）无环路有向图

（一）基本块

基本块是指程序中一顺序执行的语句序列，其中只有一个入口语句（第一个语句）和一个出口语句（最后一个语句）

对于一个基本块来说，执行时只能从其入口语句进入，从其出口语句退出

语句
出口语句	任何控制转移四元式
入口语句	所转向的目标语句

（二）划分基本块的步骤

1、求四元式序列中各个基本块的入口语句。

① 程序的第一个语句
② 能由条件或无条件转移语句转移到的语句
③ 紧跟在条件转移语句后面的语句

2、对每一入口语句，构造所属的基本块，该基本块由：

1）该入口语句到下一入口语句（不包括下一入口语句）之间的语句序列组成
2）该入口语句到一转移语句（包括该转移语句）之间的语句序列组成
3）该入口语句到一停语句（包括该停语句）之间的语句序列组成

3、凡是未包含在某一基本块中的语句，都是程序中控制流程不可达的语句，可删除它们。

例题：

对于下面给出的求最大公因子的程序，可以根据基本块的构造规则与其划分基本块

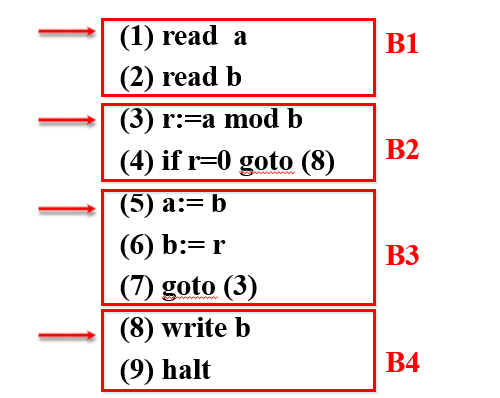
基本块构造步骤：

（1）：由规则 (1) 中的 ① 可知语句 (1) 是一个入口语句
（2）：由规则 (1) 中的 ② 可知，语句 (3) 和 (8) 均是人口语句
（3）：由规则 (1) 中的 ③ 可知，语句 (5) 是二个人口语句，可以用 “+” 在人口语句的左侧作标记。
（4）：由规则 (2) 可以划分该程序为四个基本块，它们分别是：

语句 (1)、(2) 组成的基本块 B₁
语句 (3)、(4) 组成的基本块 B₂
语句 (5)、(6) 和 (7) 组成的基本块 B₃
语句 (8) .(9) 组成的基本块 B₄

程序中在代码段左侧对各个基本块进行了标记。

（三）程序控制流程流图

定义： 以基本块为结点，控制程序流向作为有向边，画出的有向图称为流图。

特点：

具有唯一首结点的有向图
从首结点开始到流图中任何结点都有通路

如果一个结点的基本块的入口语句是程序的第一条语句，则称此结点为首结点

程序控制流程流图的表示

一个控制流程图可表示成一个三元组：
G=(N，E，n₀ )

N：所有结点(基本块)集；
E：所有有向边集；
n₀ ：首结点。

有向边：

当下述条件有一个成立时，从结点i有一有向边引向结点 j：

① 基本块 j 在程序的位置紧跟在i后，且 i 的出口语句不是无条件转移或停语句
② i 的出口是 goto(S) 或 if goto(S)，而 (S) 是 j 的入口语句

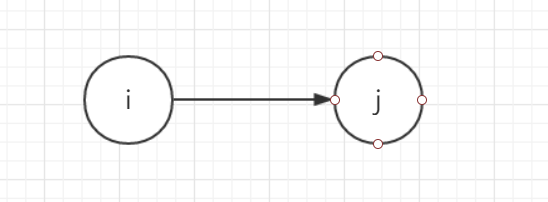
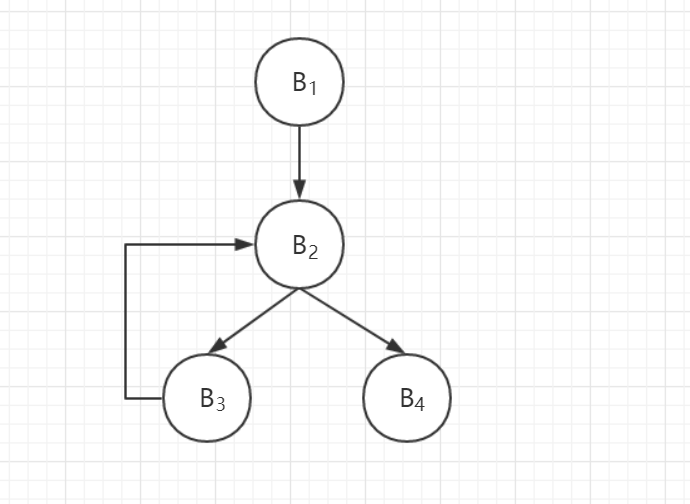
构造程序控制流图

对程序基本块：

构造以下程序控制流图：

（四）基本块的 DAG 表示

DAG Directed Acyclic Graph 无环路有向图

定义：

(1) 在一个有向图中，若结点 n_i 有弧指向结点 n_j，则 n_i 是 n_j 的父结点，n_j 是 n_i 的子结点；

(2) 若 n1,n2,…,nk 间存在有向弧 n1→n2→…→nk，则称 n1 到 nk 之间存在一条通路，若有 nk=n1，则称该通路为环路；

(3) 若有向图中任意通路都不是环路，则称该图为无环路有向图（DAG）

用来描述基本块的 DAG：

(1) 图的叶结点以一标识符或常数做标记，表示该结点代表该变量或常数的值。

(2) 图的内部结点以一运算符作为标记；

(3) 图中各个结点上可能附加一个或多个标识符，表示这些标识符具有该结点所代表的值，简称附标。

四元式对应的 DAG 结点形式

按其四元式对应结点的后继个数分成四种类型：0型、1型、2型、3型

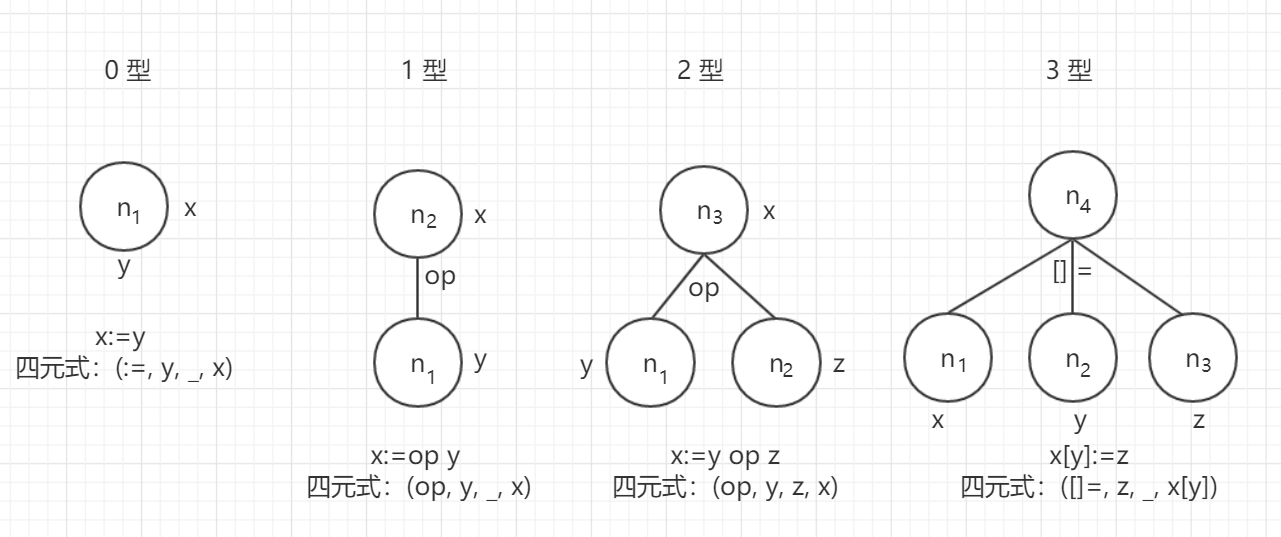
（五）DAG 图构造例题

对于基本块 P

（1）S₀ := 2
（2）S₄ := 2
（3）S₁ := 1.5
（4）S₂ := T-C
（5）S₃ := T+C
（6）S₅ := S₃
（7）R := 2/S₃
（8）S₆ := R
（9）H := R*S₂

（1）试用 DAG 进行优化并重写基本块
（2）假定只有 R，H 在基本块出口是活跃的，试写出优化后的 4 元式序列
（只需要还原活跃变量）

解析：

（1）画出 DAG 图如下：

画图的步骤就是：根据基本块，一部一部组装

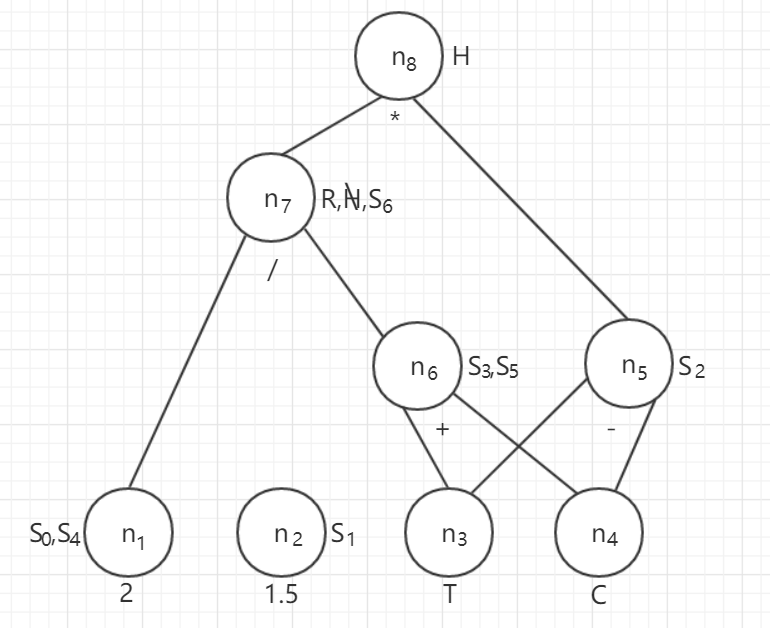
（2）假定只有 R，H 在基本块出口是活跃的，试写出优化后的 4 元式序列
（只需要还原活跃变量）

优化后的 4 元式代码可以写为：
（1）S₂ := T-C
（2）S₃ := T+C
（3）R := 2/S₃
（4）H := R*S₂

解释：

与原来的基本块相比较可以看出：

原基本块中的 (2) 和 (7) 中的已知量都已经合并。因为 (2) 中 S₄ := 2，(7) 中用 2，所以合并。
(5) 和 (8) 中的公共子表达式 T+C 只在 (5) 中计算一次，在 (8) 中直接引用其结果，所以删除了多余运算。
(6) 中的无用赋值已被删除。S₅ := S₃，S₅ 后面没有再用，所以就和 S₃ 一起表示。

除了可以应用 DAG 进行上述的优化外，还可以从基本块的 DAG 中得到一些其他信息：

DAG 叶结点上标记的标识符是在该基本块之前的基本块内被定值，并在该基本块内被引用的标识符。
DAG 各结点上的附加标识符是在基本块内被定值，并可以在基本块后被引用的标识符。

如果确认某结点的一个附加标记在基本块后不会被引用，则该标识符的定值语句可以作为死代码被删除。

假设上面例子中 S₀~S₆。在基本块后面都不会被引用只有 R, H 在基本块出口是活跃的则优化后的四元式序列可以写为：
（1）S₂ := T-C
（2）S₃ := T+C
（3）R := 2/S₃
（4）H := R*S₂