解题报告：hdu 2073 无限的路

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2073

Problem Description

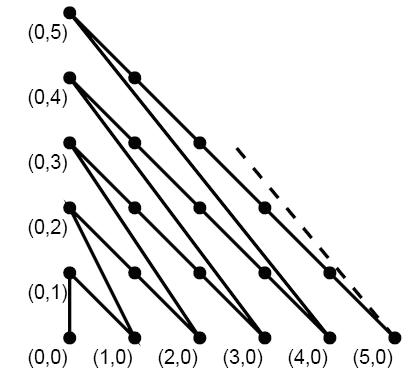甜甜从小就喜欢画图画，最近他买了一支智能画笔，由于刚刚接触，所以甜甜只会用它来画直线，于是他就在平面直角坐标系中画出如下的图形：甜甜的好朋友蜜蜜发现上面的图还是有点规则的，于是他问甜甜：在你画的图中，我给你两个点，请你算一算连接两点的折线长度（即沿折线走的路线长度）吧。

Input

第一个数是正整数N（≤100）。代表数据的组数。 每组数据由四个非负整数组成x1，y1，x2，y2；所有的数都不会大于100。

Output

对于每组数据，输出两点(x1,y1),(x2,y2)之间的折线距离。注意输出结果精确到小数点后3位。

Sample Input

5

0 0 0 1

0 0 1 0

2 3 3 1

99 99 9 9

5 5 5 5

Sample Output

1.000

2.414

10.646

54985.047

0.000

解题思路：这又是一道规律题，每一点都保存前面的值,求两点之间的距离就是各点的和值相减得到的绝对值就行了。仔细观察图片可以得出计算两点之间的距离可以拆分为两部分组成，一个是sqrt(2)的倍数，另一个是sqrt[i*i+(i+1)*(i+1)]，其中i是从0~（不包括）x+y（点（x，y）），发现规律后再敲一遍代码，思路清晰。

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 double as(int x,int y)//计算(0,0)到(x,y)的折线距离
 {
     double t=sqrt(),ans=;
     for(int i=;i<x+y;i++)//由规律得到先对sqrt(2)进行相乘
         ans+=t*i;
     ans+=t*x;//加上此点的横坐标x乘以t即可
     for(int i=;i<x+y;i++)//相邻边的平方和
         ans+=sqrt(i*i+(i+)*(i+));//再加上这个规律
     return ans;
 }
 int main()
 {
     int N,x1,y1,x2,y2;//两个坐标点
     cin>>N;
     while(N--){
         cin>>x1>>y1>>x2>>y2;
         printf("%.3f\n",fabs(as(x2,y2)-as(x1,y1)));//相减的绝对值
     }
     return ;
 }