hdu 6035(树形dp）

题意：给你棵树，树上每个节点都有颜色，每条路径上有m种颜色  问你所有路径上出现的颜色的和

思路：答案求的是每种颜色对路径的贡献  我们可以反过来每种颜色不经过的路径的条数

假设根节点的颜色为x  我们就可以知道不过x颜色的路径一定不经过这个根节点 和不经过这个子树中颜色为x的节点

所有树形dp。。。。。。。

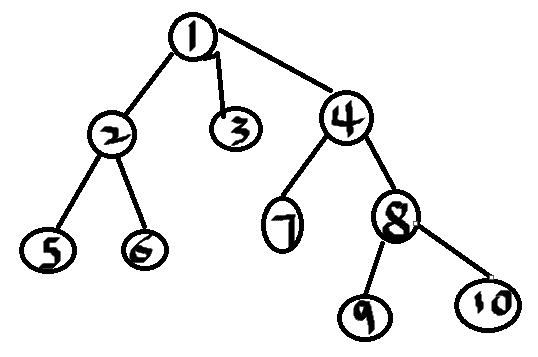
son[u]统计的是以u的根节点的子树的大小  节点的颜色为a[i]   sum[a[i]]为在以i节点为根节点颜色a[i]的子树大小， 比如 1 8节点的颜色相同  x颜色没有经过的节点为1的儿子-sum[a[8]];

sum[a[8]]是可以在DFS中过程得到的 没有经过的点有y个  路径就有y*(y-1)/2;

所有我们在DFS一遍就能求出所有颜色没有经过的路径数目

答案就是所有的颜色经过所有的路径-所有的点没有经过的路径数目

我感觉dfs解释的有点牵强  具体看代码把 比较好理解

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cstdlib>
 #include<string.h>
 #include<set>
 #include<vector>
 #include<queue>
 #include<stack>
 #include<map>
 #include<cmath>
 typedef long long ll;
 typedef unsigned long long LL;
 using namespace std;
 const double PI=acos(-1.0);
 const double eps=0.0000000001;
 const int N=+;
 int a[N],b[N];
 int n,m;
 int tot;
 int head[N];
 ll ans;
 int son[N];
 int sum[N];
 struct node{
     int to,next;
 }edge[N<<];
 void init(){
     memset(head,-,sizeof(head));
     memset(sum,,sizeof(sum));
     tot=;
 }
 void add(int u,int v){
     edge[tot].to=v;
     edge[tot].next=head[u];
     head[u]=tot++;
 }
 void DFS(int u,int fa){
     son[u]=;
     ll t=sum[a[u]];
     ll c=;
     for(int i=head[u];i!=-;i=edge[i].next){
         int v=edge[i].to;
         if(v==fa)continue;
         DFS(v,u);
         son[u]=son[v]+son[u];
         ll temp=son[v]-(sum[a[u]]-t);
         t=sum[a[u]];
         c=c+temp;
         ans=ans-(temp-)*temp/;
     }
     sum[a[u]]+=c+;
 }
 int main(){
     int tt=;
     while(scanf("%d",&n)!=EOF){
         init();
         for(int i=;i<=n;i++)scanf("%d",&a[i]);
         for(int i=;i<n;i++){
             int u,v;
             scanf("%d%d",&u,&v);
             add(u,v);
             add(v,u);
         }
         ans=(ll)n*(n-)*n/;
         DFS(,);
         for(int i=;i<=n;i++){
             ll temp=n-sum[i];
             ans=ans-(temp-)*temp/;
         }
         printf("Case #%d: %lld\n", tt++, ans);
     }
 }