HDU1693 Eat the Trees —— 插头DP

题目链接：https://vjudge.net/problem/HDU-1693

Eat the Trees

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4505    Accepted Submission(s): 2290

Problem Description

Most of us know that in the game called DotA(Defense of the Ancient), Pudge is a strong hero in the first period of the game. When the game goes to end however, Pudge is not a strong hero any more.
So Pudge’s teammates give him a new assignment—Eat the Trees!

The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.

Now Pudge has a question, how many ways are there to eat the trees?
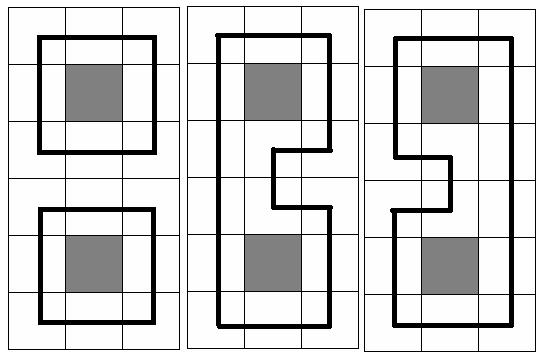
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))

 

Input

The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.

 

Output

For each case, you should print the desired number of ways in one line. It is guaranteed, that it does not exceed 2⁶³ – 1. Use the format in the sample.

 

Sample Input

2
6 3
1 1 1
1 0 1
1 1 1
1 1 1
1 0 1
1 1 1
2 4
1 1 1 1
1 1 1 1

 

Sample Output

Case 1: There are 3 ways to eat the trees.
Case 2: There are 2 ways to eat the trees.

 

Source

2008 “Sunline Cup” National Invitational Contest

 

Recommend

wangye

题意：

用一个或者多个回路去经过所有空格子，问总共有多少种情况？

题解：

有关路径的插头DP。

1.由于只需要记录轮廓线上m+1个位置的插头情况（0或1），且m<=11，2^11 = 2048，故可以用二进制对轮廓线的信息进行压缩。

2.接着就是人工枚举了。

对于如何维护轮廓线的理解：

1.对于棋盘。我们需要将其开始下标设为1（方便维护轮廓线）。

2.将要处理第i行第1列的时候，它的左插头的信息记录在第0位，它的上插头的信息刚好记录在第1位。

3.当处理完第i行第1列的时候，我们就把它的左插头改为下插头，上插头改为右插头。这样，对于第i行第2列来说，它的左插头记录在第1位，上插头记录在第2位。所以可以总结出：对于当前要转移的格子a[i][j]，它的左插头的信息记录在第j-1位，它的上插头记录在第j位。

4.当转移完第i行最后一个格子的时候，左插头就位于轮廓线的最后位置，即其信息记录在最高位。而我们在转到下一行第一列的时候，由于a[i+1][1]的左插头是记录在第0位的，所以就需要把最高位的移到第0位，后面的位又往后移动一位，即左移。我们又知道：第一列的格子是没有左插头的，所以，在转行的时候，有效的轮廓线是没有左插头轮廓线，我们取这些有效的轮廓线，并对其压缩信息左移一位即可。

写法一：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = 1e5;

 int n, m, Map[][];
 LL dp[][][<<];

 int main()
 {
     int T, kase = ;
     scanf("%d", &T);
     while(T--)
     {
         scanf("%d%d", &n, &m);
         for(int i = ; i<=n; i++)
         for(int j = ; j<=m; j++)
             scanf("%d", &Map[i][j]);

         memset(dp, , sizeof(dp));
         dp[][m][] = ;      //初始状态
         for(int i = ; i<=n; i++)
         {
             //可知转移完行末的格子后，左插头在轮廓线上最后一个位置，即其信息记录在最后一个位
             //由于第一列的格子肯定没有左插头，所以只需枚举到(1<<m)-1，以去除掉含有左插头的情况。
             for(int s = ; s<(<<m); s++)
                 dp[i][][s<<] = dp[i-][m][s];

             for(int j = ; j<=m; j++)
             {
                 for(int s = ; s<(<<m+); s++) //枚举上一个格子的所以状态，即当前格子的轮廓线
                 {
                     int up = <<j;  //上插头
                     int left = <<(j-);    //左插头
                     bool have_up = s&up;
                     bool have_left = s&left;

                     if(!Map[i][j])  //当前格子不可行
                     {
                         if( !have_up && !have_left )  //当没有插头时，才能转移
                             dp[i][j][s] += dp[i][j-][s];
                     }
                     else        //当前格子可行
                     {
                         if( !have_up && !have_left )    //两个格子都不存在，新建分量
                         {
                             dp[i][j][s^up^left] += dp[i][j-][s];
                         }
                         else if( have_up && !have_left )    //有上插头无左插头
                         {
                             dp[i][j][s] += dp[i][j-][s];   //往右延伸
                             dp[i][j][s^up^left] += dp[i][j-][s];   //往下延伸
                         }
                         else if( !have_up && have_left ) //无上插头有左插头
                         {
                             dp[i][j][s] += dp[i][j-][s];   //往下延伸
                             dp[i][j][s^up^left] += dp[i][j-][s]; //往右延伸
                         }
                         else    //两个插头都存在，只能合并分量
                         {
                             dp[i][j][s^up^left] += dp[i][j-][s];
                         }
                     }
                 }
             }
         }
         printf("Case %d: There are %lld ways to eat the trees.\n", ++kase, dp[n][m][]);
     }
 }

写法二（写法一的简写）：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = 1e5;

 int n, m, Map[][];
 LL dp[][][<<];

 int main()
 {
     int T, kase = ;
     scanf("%d", &T);
     while(T--)
     {
         scanf("%d%d", &n, &m);
         for(int i = ; i<=n; i++)
         for(int j = ; j<=m; j++)
             scanf("%d", &Map[i][j]);

         memset(dp, , sizeof(dp));
         dp[][m][] = ;      //初始状态
         for(int i = ; i<=n; i++)
         {
             //可知转移完行末的格子后，左插头在轮廓线上最后一个位置，即其信息记录在最后一个位
             //由于第一列的格子肯定没有左插头，所以只需枚举到(1<<m)-1，以去除掉含有左插头的情况。
             for(int s = ; s<(<<m); s++)
                 dp[i][][s<<] = dp[i-][m][s];

             for(int j = ; j<=m; j++)
             {
                 for(int s = ; s<(<<m+); s++) //枚举上一个格子的所以状态，即当前格子的轮廓线
                 {
                     int up = <<j;  //上插头
                     int left = <<(j-);    //左插头
                     bool have_up = s&up;
                     bool have_left = s&left;

                     if(!Map[i][j])  //当前格子不可行
                     {
                         if( !have_up && !have_left )  //当没有插头时，才能转移
                             dp[i][j][s] += dp[i][j-][s];
                     }
                     else        //当前格子可行
                     {
                         dp[i][j][s^up^left] += dp[i][j-][s];
                         if( (have_up&&!have_left) || (!have_up&&have_left) )
                             dp[i][j][s] += dp[i][j-][s];
                     }
                 }
             }
         }
         printf("Case %d: There are %lld ways to eat the trees.\n", ++kase, dp[n][m][]);
     }
 }

对写法一用哈希表优化了一下，但是过不了，差不出错误。先放着：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = 1e5;
 const int HASH = 1e4;

 int n, m, Map[][];

 struct
 {
     int size, head[HASH], next[MAXN];
     int state[MAXN];
     LL sum[MAXN];

     void init()
     {
         size = ;
         memset(head, -, sizeof(head));
     }

     void insert(int status, LL Sum)
     {
         int u = status%HASH;
         for(int i = head[u]; i!=-; i = next[i])
         {
             if(state[i]==status)
             {
                 sum[i] += Sum;
                 return;
             }
         }
         state[size] = status;   //头插法
         sum[size] = Sum;
         next[size] = head[u];
         head[u] = size++;
     }

 }Hash_map[];

 void transfer(int i, int j, int cur)
 {
     for(int k = ; k<Hash_map[cur].size; k++)
     {
         int s = Hash_map[cur].state[k];
         LL Sum = Hash_map[cur].sum[k];

         int up = <<j;
         int left = <<(j-);
         bool have_up = s&up;
         bool have_left = s&left;

         if(!Map[i][j])
         {
             Hash_map[cur^].insert(s<<(j==m), Sum);
         }
         else
         {
             if( !have_up && !have_left )
             {
                 if(Map[i+][j] && Map[i][j+])
                     Hash_map[cur^].insert((s^up^left)<<(j==m), Sum);
             }
             else if( have_up && !have_left )    //有上插头无左插头
             {
                 if(Map[i][j+])
                     Hash_map[cur^].insert(s<<(j==m), Sum);
                 if(Map[i+][j])
                     Hash_map[cur^].insert((s^up^left)<<(j==m), Sum);
             }
             else if( !have_up && have_left ) //无上插头有左插头
             {
                 if(Map[i][j+])
                     Hash_map[cur^].insert((s^up^left)<<(j==m), Sum);
                 if(Map[i+][j])
                     Hash_map[cur^].insert(s<<(j==m), Sum);
             }
             else
             {
                 Hash_map[cur^].insert((s^up^left)<<(j==m), Sum);
             }
         }
     }
 }

 int main()
 {
     int T, kase = ;
     scanf("%d", &T);
     while(T--)
     {
         scanf("%d%d", &n, &m);
         memset(Map, , sizeof(Map));
         for(int i = ; i<=n; i++)
         for(int j = ; j<=m; j++)
             scanf("%d", &Map[i][j]);

         int cur = ;
         Hash_map[cur].init();
         Hash_map[cur].insert(, );
         for(int i = ; i<=n; i++)
         {
             for(int j = ; j<=m; j++)
             {
                 Hash_map[cur^].init();
                 transfer(i, j, cur);
                 cur ^= ;
             }
         }
         printf("Case %d: There are %lld ways to eat the trees.\n", ++kase, Hash_map[cur].sum[]);
     }
 }