这是我见过最通俗易懂的SVD（奇异值分解）算法介绍

线性代数是机器学习领域的基础，其中一个最重要的概念是奇异值分解（SVD），本文尽可能简洁的介绍SVD（奇异值分解）算法的基础理解，以及它在现实世界中的应用。

SVD是最广泛使用的无监督学习算法之一，它在许多推荐系统和降维系统中居于核心位置，这些系统是全球公司如谷歌、Netflix、Facebook、YouTube等的核心技术。

简单来说，SVD是将一个任意矩阵分解为三个矩阵。所以如果我们有一个矩阵A，那么它的SVD可以表示为：

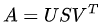
A是矩阵，U是的正交矩阵，是的非负对角矩阵，是的正交矩阵。

U也被称为左奇异向量，S为奇异值，V为右奇异向量。

带维度的奇异值分解：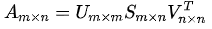

用矩阵表示奇异值分解：

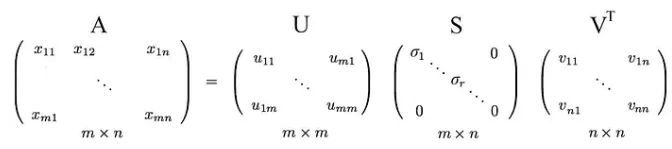
我们通常将具有较大特征值的向量排列在前，而较小特征值的向量则排在后面。

特征值与向量的对应关系：

与特征值分解相比，奇异值分解可以应用于非方阵。在SVD中，U和 V 对于任何矩阵都是可逆的，并且它们是正交归一的，这是我们所喜爱的特性。虽然这里不进行证明，但我们可以告诉你，奇异值比特征值在数值上更稳定。

为了更好地理解，我们通过一个例子演示SVD。

假设我们有非方阵A：

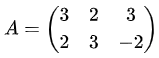
我们计算矩阵与转置矩阵的乘积，有：

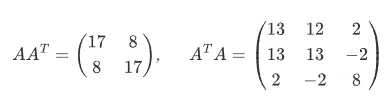
求解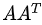的特征值和特征向量：

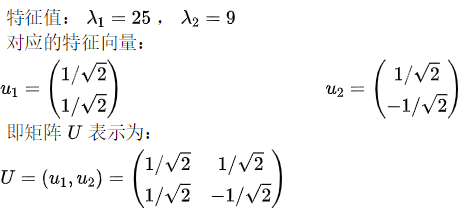
求解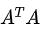的特征值和特征向量：

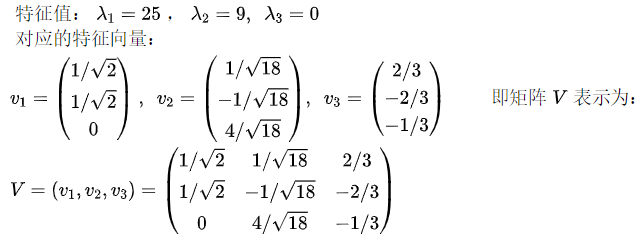
奇异值是正特征值的平方根，即5和3。因此非方阵A的SVD分解为：

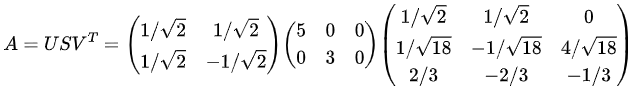
SVD分解证明

最后一个方程等价于求矩阵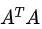的特征向量，我们只需将所有特征向量放入一个矩阵中，矩阵S则是包含特征值的对角矩阵。

SVD的另一种表述

SVD降维

SVD应用

1.图像降维

2.特征脸

3.降低噪声

结论

我真的觉得奇异值分解（SVD）被低估了。它是线性代数中一个非常重要的基础概念，而且它的应用非常酷！相信我，我们看到的只是 SVD 众多用途中的一小部分。有什么问题，欢迎讨论！

原文链接：这是我见过最通俗易懂的SVD（奇异值分解）算法介绍