N-gram基本原理
N-gram模型是一种语言模型(Language Model,LM),语言模型是一个基于概率的判别模型,它的输入是一句话(单词的顺序序列),输出是这句话的概率,即这些单词的联合概率(joint probability)。

N-gram本身也指一个由N个单词组成的集合,考虑单词的先后顺序,且不要求单词之间互不相同。常用的有 Bi-gram (N=2N=2N=2) 和 Tri-gram (N=3N=3N=3),一般已经够用了。例如在上面这句话里,我可以分解的 Bi-gram 和 Tri-gram :
Bi-gram : {I, love}, {love, deep}, {love, deep}, {deep, learning}
Tri-gram : {I, love, deep}, {love, deep, learning}N-gram中的概率计算

联合概率的简单推导过程:A,B,C三个有顺序的句子。
由于
P(C/(A,B))=P(A,B,C)/P(A,B)
P(B/A) = P(A,B)/P(B)
所以
P(C/(A,B))=P(A,B,C)/(P(B/A) *P(B))
P(A,B,C) = P(C/(A,B))*P(B/A) *P(B)
所以我们可以很容易的得到上面的多个单词的联合概率,但是由于存在参数空间过大等问题,我们可以仅仅考虑之前的一个或者几个词的前提条件的联合概率,可以降低时间复杂度,减少计算量。

然后通过极大似然函数求解上面的概率值
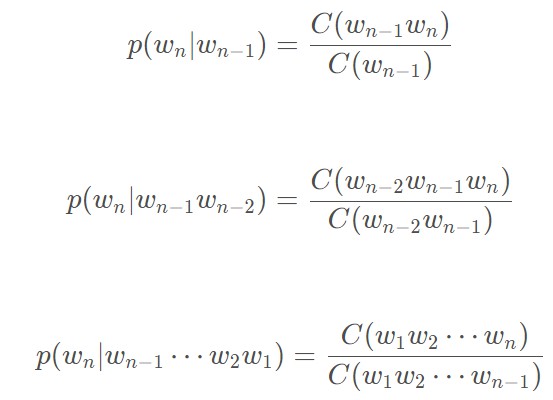
是从整个数据库中去计算上述的概率值,而不是一整句话。
1、可以用于词性标注,类似成多分类的情况:
例如:我爱中国!
判断爱的词性可以通过P(词性i/(名词我出现,爱字出现))=P(名词我出现,爱字不同的词性)/P(名词的我出现,爱字所有出现的次数)
2、可以用于垃圾短信分类:

- 步骤一:给短信的每个句子断句。
- 步骤二:用N-gram判断每个句子是否垃圾短信中的敏感句子。
- 步骤三:若敏感句子个数超过一定阈值,认为整个邮件是垃圾短信。
3、用于分词作用
在NLP中,分词的效果很大程度上影响着模型的性能,因此分词甚至可以说是最重要的工程。用N-gram可以实现一个简单的分词器(Tokenizer)。同样地,将分词理解为多分类问题:X表示有待分词的句子,Yi表示该句子的分词方案:
X="我爱深度学习"
Y1={"我","爱深","度学习"}
Y2={"我爱","深","度学","习"}
Y3={"我","爱","深度学习"}
p(Y1)=p(我)p(爱深∣我)p(度学习∣爱深)
p(Y2)=p(我爱)p(深∣我爱)p(度学∣深)p(习∣度学)
p(Y3)=p(我)p(爱∣我)p(深度学习∣爱)
三个概率中,“我爱”可能在语料库中比较常见,因此p(爱∣我)p(爱|我)p(爱∣我)会比较大,然而“我爱深”这样的组合比较少见,
于是p(爱深∣我)p(爱深|我)p(爱深∣我)和p(深∣我爱)p(深|我爱)p(深∣我爱)都比较小 ,因此第三种分词方案最佳。
语音识别和机器翻译中也用到。
N-gram中的数据平滑方法
由于N-gram的N越大,模型效果越好。这在直观意义上是说得通的,毕竟依赖的词越多,我们获得的信息量越多,对未来的预测就越准确。然而,语言是有极强的创造性的(Creative),当N变大时,更容易出现这样的状况:某些n-gram从未出现过,这就是稀疏问题。
n-gram最大的问题就是稀疏问题(Sparsity)。例如,在bi-gram中,若词库中有20k个词,那么两两组合就有近2亿个组合。其中的很多组合在语料库中都没有出现,根据极大似然估计得到的组合概率将会是0,从而整个句子的概率就会为0。最后的结果是,我们的模型只能计算零星的几个句子的概率,而大部分的句子算得的概率是0,这显然是不合理的。
因此,我们要进行数据平滑(data Smoothing),数据平滑的目的有两个:一个是使所有的N-gram概率之和为1,使所有的n-gram概率都不为0。它的本质,是重新分配整个概率空间,使已经出现过的n-gram的概率降低,补充给未曾出现过的n-gram。


为了解决稀疏问题和参数空间过大的问题,从机器学习的角度看N-gram模型:


vi*hi代表利用神经网络学习出来的预测值,利用预测值与真实的概率值的差值作为损失函数。
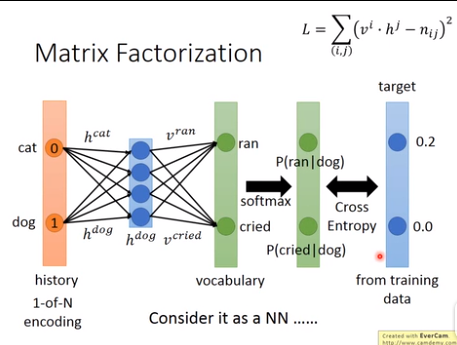
v和h通过上述这种网络结构进行学习,然后经过softmax函数计算出概率值然后和目标值做差进行更新参数v,h。
每一个神经元在上一个单词的前提下预测此单词的概率,最终把所有的计算出来,相乘就是最终的结果。在RNN上的应用
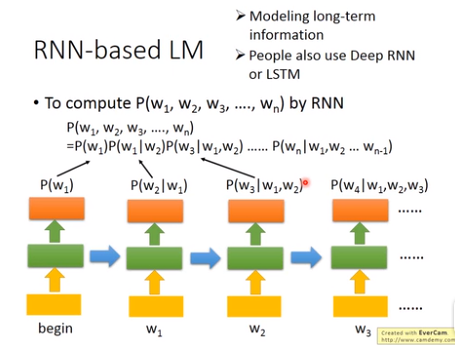
RNN结构比神经网络结构好是因为可以减少参数。
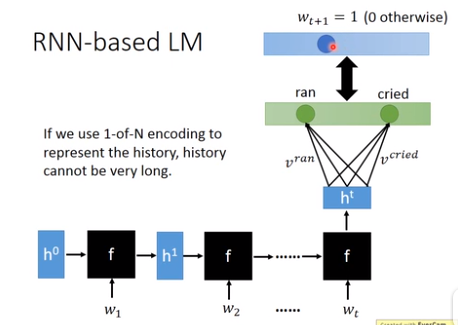
N-gram基本原理的更多相关文章
- Ognl表达式基本原理和使用方法
Ognl表达式基本原理和使用方法 1.Ognl表达式语言 1.1.概述 OGNL表达式 OGNL是Object Graphic Navigation Language(对象图导航语言)的缩写,他是一个 ...
- Android自定义控件之基本原理
前言: 在日常的Android开发中会经常和控件打交道,有时Android提供的控件未必能满足业务的需求,这个时候就需要我们实现自定义一些控件,今天先大致了解一下自定义控件的要求和实现的基本原理. 自 ...
- HMM基本原理及其实现(隐马尔科夫模型)
HMM(隐马尔科夫模型)基本原理及其实现 HMM基本原理 Markov链:如果一个过程的“将来”仅依赖“现在”而不依赖“过去”,则此过程具有马尔可夫性,或称此过程为马尔可夫过程.马尔可夫链是时间和状态 ...
- 动态令牌-(OTP,HOTP,TOTP)-基本原理
名词解释和基本介绍 OTP 是 One-Time Password的简写,表示一次性密码. HOTP 是HMAC-based One-Time Password的简写,表示基于HMAC算法加密的一次性 ...
- ZooKeeper基本原理
ZooKeeper简介 ZooKeeper是一个开放源码的分布式应用程序协调服务,它包含一个简单的原语集,分布式应用程序可以基于它实现同步服务,配置维护和命名服务等. ZooKeeper设计目的 1. ...
- GBDT的基本原理
这里以二元分类为例子,给出最基本原理的解释 GBDT 是多棵树的输出预测值的累加 GBDT的树都是 回归树 而不是分类树 分类树 分裂的时候选取使得误差下降最多的分裂 计算的技巧 最终分裂收益按照下面 ...
- 全文检索引擎 Solr 部署与基本原理
全文检索引擎 Solr 部署与基本原理 搜索引擎Solr环境搭建实例 关于 solr , schema.xml 的配置说明 全文检索引擎Solr系列-–全文检索基本原理 一.搜索引擎Solr环境搭建实 ...
- 相机位姿估计0:基本原理之如何解PNP问题
关键词:相机位姿估计 PNP问题求解 用途:各种位姿估计 文章类型:原理 @Author:VShawn(singlex@foxmail.com) @Date:2016-11-18 @Lab: CvLa ...
- geohash基本原理
geohash基本原理是将地球理解为一个二维平面,将平面递归分解成更小的子块,每个子块在一定经纬度范围内拥有相同的编码,这种方式简单粗暴,可以满足对小规模的数据进行经纬度的检索 目录: 经纬度常识 认 ...
- Struts框架——(一)用Servlet + JSP演示Struts基本原理
一. 用Servlet + JSP演示Struts基本原理 struts是开源项目.它通过采用 Java Servlet/JSP 技术,实现了基于Java EE Web应用的MVC的应用框架.Stru ...
随机推荐
- uniapp权限判断
写法如下 // 检查是否有写入外部存储的权限 function writeExternalStoragePermission() { return new Promise((resolve, reje ...
- Flutter Stream的使用
Flutter Stream的使用 首先,来了解一下stream是什么 异步数据事件的来源. 流提供了一种接收一系列事件的方法.每个事件要么是一个数据事件,也称为流的元素,要么是一个错误 事件,即某事 ...
- Springboot-actuator的常用endpoint的使用说明
目的 监控并管理应用程序监控:让我们去发现和了解程序的运行状况各种指标管理:比如说通过Actuator去做一个shutdown功能,通过访问一个特定的url去操作,默认是不开启的,另外 还可以在运行的 ...
- java正则表达式(find()和 matches())
1.find()方法是部分匹配,是查找输入串中与模式匹配的子串,如果该匹配的串有组还可以使用group()函数. matches()是全部匹配,是将整个输入串与模式匹配,如果要验证一个输入的数据是否为 ...
- 管理员应了解的 SIEM解决方案七大功能 !
SIEM解决方案已成为企业网络安全武器库中不可或缺的一部分.但由于SIEM功能过于复杂且架构难以理解,企业往往SIEM的潜在功能.遗憾的是,他们忽视的潜在功能正是解开企业网络合规的重要部分. 例如, ...
- Unity 3D更换默认脚本编辑器VisualStudio
由于VisualStudio 30天试用到期了,所有不能编辑Unity 3D脚本.需要更换成Notepad++ 打开Unity 3D顶部菜单 点击编辑(Editor)->Preferences- ...
- Qt音视频开发45-音视频类结构体参数的设计
一.前言 视频监控内核组件重构和完善花了一年多时间,整个组件个人认为设计的最好的部分就是各种结构体参数的设计,而且分门别类,有枚举值,也有窗体相关的结构体参数,解码相关的结构体参数,同时将部分常用的结 ...
- IM开发者的零基础通信技术入门(十二):上网卡顿?网络掉线?一文即懂!
[来源申明]本文引用了微信公众号"鲜枣课堂"的<上网慢?经常掉线?这篇文章告诉你该怎么办!>文章内容.为了更好的内容呈现,即时通讯网在引用和收录时内容有改动,转载时请注 ...
- ConcurrentHashMap源码分析-JDK18
前言 ConcurrentHashMap是一个线程安全的HashMap,主要用于解决HashMap中并发问题. 在ConcurrentHashMap之前,也有线程安全的HashMap,比如HashTa ...
- WPFMediaKit --WPF项目中 调用摄像头拍照
<Window x:Class="WpfApp1.MainWindow" xmlns="http://schemas.microsoft.com/winfx/200 ...
