Python3-递归函数

什么是递归？

递归，就是函数在运行的过程中调用自己。

代码示例

def recursion(n):

    print(n)

    recursion(n+)

recursion()

出现的效果就是，这个函数在不断的调用自己，每次调用就n+1,相当于循环了。

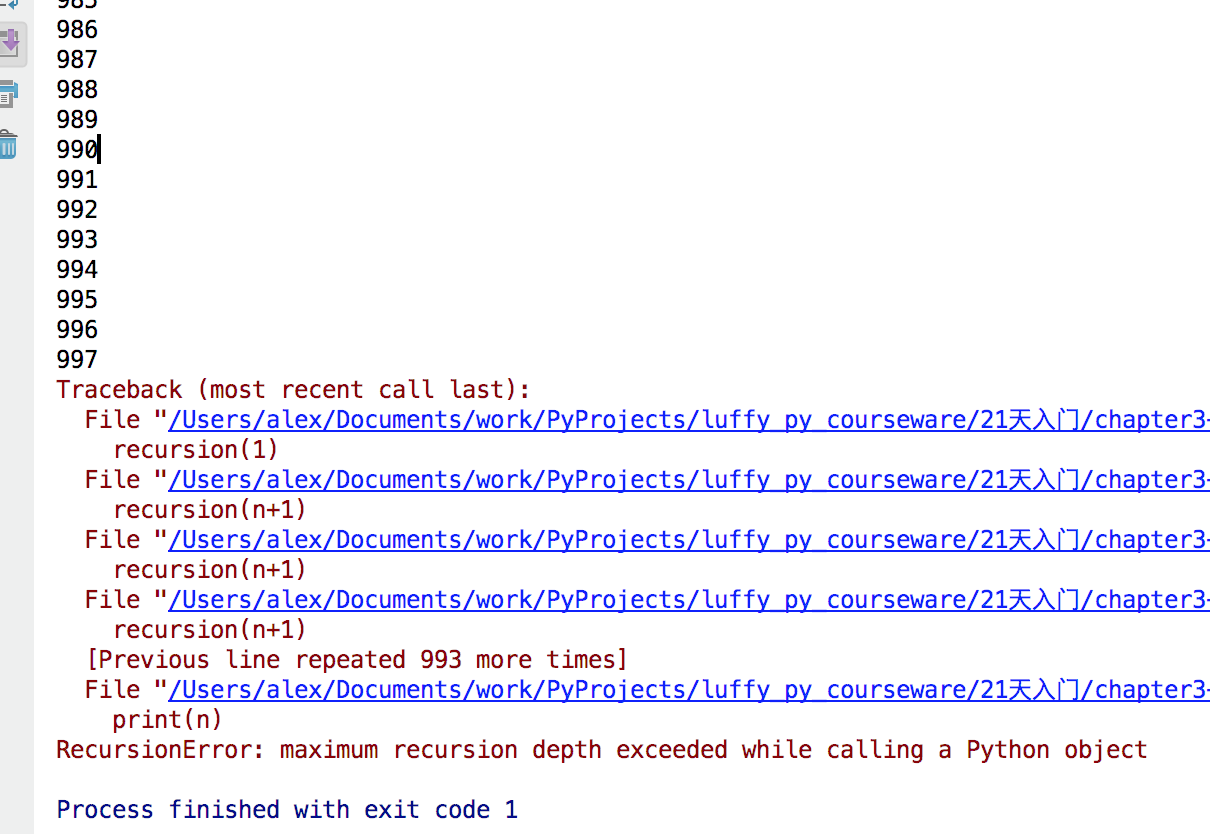
可是为何执行了900多次就出错了呢？还说超过了最大递归深度限制，为什么要限制呢？

通俗来讲，是因为每个函数在调用自己的时候还没有退出，占内存，多了肯定会导致内存崩溃。

本质上讲呢，在计算机中，函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出。

递归的特点

让我们通过现象来看本质，下面是是用递归写的，让10不断除以2，直到0为止。

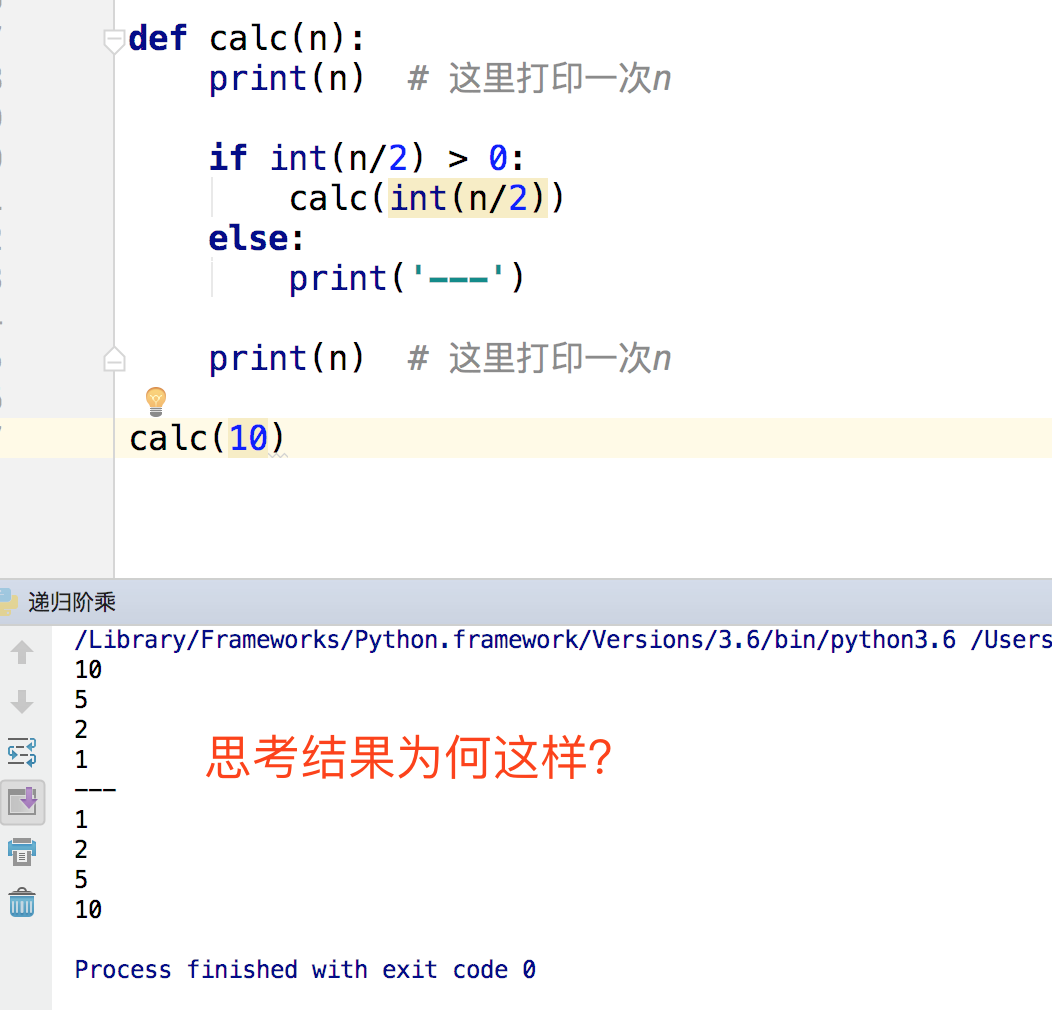
打印的是1，然后最里层的函数就结束了，结束后会返回到之前调用它的位置。即上一层，上一层打印的是2，再就是5，再就是10，即最外层函数，然后结束，总结，这个递归就是一层层进去，还要一层层出来。

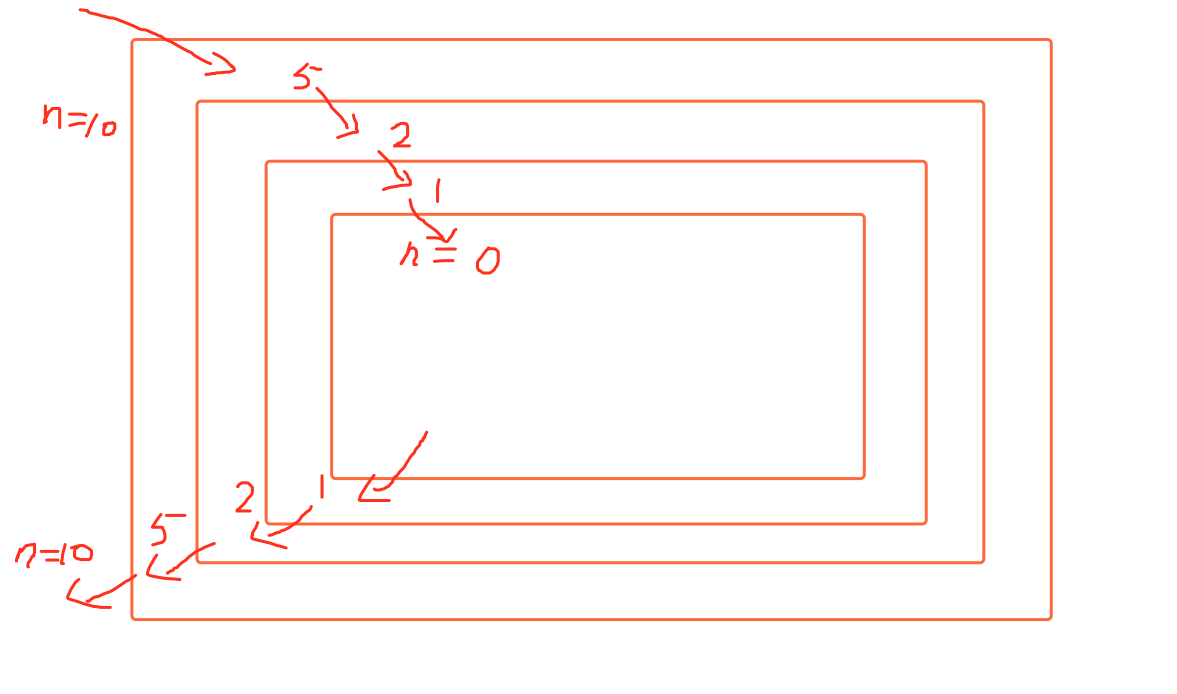
通过上面的例子，我们可以总结递归几个特点：

必须有一个明确的结束条件，要不就会变成死循环了，最终撑爆系统
每次进入更深一层递归时，问题规模相比上次递归都应有所减少
递归执行效率不高，递归层次过多会导致栈溢出

递归有什么用呢？

可以用于解决很多算法问题，把复杂的问题分成一个个小问题，一一解决。

比如求斐波那契数列、汉诺塔、多级评论树、二分查找、求阶乘等。用递归求斐波那契数列、汉诺塔对初学者来讲可能理解起来不太容易，所以我们用阶乘和二分查找来给大家演示一下。

求阶乘

任何大于1的自然数n阶乘表示方法：
n!=1×2×3×……×n
或
n!=n×(n-1)!

即举例：4! = 4x3x2x1 = 24

用递归代码来实现

def factorial(n):

    if n == : #是0的时候，就运算完了

        return

    return n * factorial(n-) # 每次递归相乘，n值都较之前小1

d = factorial()

print(d)

2分查找

在一个已排序的数组data_set中，使用二分查找n，假如这个数组的范围是[low...high]，我们要的n就在这个范围里。查找的方法是拿low到high的正中间的值，我们假设是mid，来跟n相比，如果mid>n，说明我们要查找的n在前数组data_set的前半部，否则就在后半部。无论是在前半部还是后半部，将那部分再次折半查找，重复这个过程，知道查找到n值所在的地方。

data_set = list(range())

def b_search(n,low,high,d):

    mid = int((low+high)/) # 找到列表中间的值

    if low == high:

        print("not find")

        return

    if d[mid] > n: # 列表中间值>n, 代数要找的数据在左边

        print("go left:",low,high,d[mid])

        b_search(n,low,mid,d) # 去左边找

    elif d[mid] < n: # 代数要找的数据在左边

        print("go right:",low,high,d[mid])

        b_search(n,mid+,high,d) # 去右边找

    else:

        print("find it ", d[mid])

b_search(, ,len(data_set),data_set)

go right:

go right:

go right:

go right:

go right:

go right:

not find

最多将会操作7次，其实因为每一次我们都抛掉当前确定的区间的一半的区间作为不可能解部分，那么相当于求最多操作次数，就是在区间内，最多将有多少个一半可以抛去、那么就是将100一直除以2，直到不能除为止。

那么这个运算过程，其实就是相当于求了一个log2（100）≈7。

补充：

在讲特性时，我们说递归效率不高，因为每递归一次，就多了一层栈，递归次数太多还会导致栈溢出，这也是为什么python会默认限制递归次数的原因。但有一种方式是可以实现递归过程中不产生多层栈的，即尾递归，

尾递归

在函数最尾部有return，return值是递归形式调用，且返回值与上一层函数无任何依赖。

尾递归例子

def calc(n):

    print(n - )

    if n > -:

        return calc(n-)

我们之前求的阶乘是尾递归么？

def factorial(n):

    if n == : #是0的时候，就运算完了

        return

    return n * factorial(n-) # 每次递归相乘，n值都较之前小1

d = factorial()

print(d)

上面的这种递归计算最终的return操作是乘法操作。所以不是尾递归。因为每个活跃期的返回值都依赖于用n乘以下一个活跃期的返回值，因此每次调用产生的栈帧将不得不保存在栈上直到下一个子调用的返回值确定。