直接插入排序算法的C++实现

直接插入算法：每趟将一个待排序的关键字按照其值的大小插入到已经排好的部分有序序列的适当位置上，直到所有待排序的关键字都被插入到有序序列中为止。

理论上，在直接插入排序中第二层循环是可以提前结束的，即某个元素在寻找自己合适位置时并未循环遍历到序列最前端。

这是直接插入排序和简单选择排序最大的不同。也是直接插入排序和简单选择排序同为时间复杂度O(n²)，但是直接插入排序效率更高的原因。

尤其是在待排序数据基本有序的时候，这种优势将极其明显。甚至此时直接插入排序要比时间复杂度为O(nlogn)的排序算法更加高效。

#include<iostream>
#include<string>
using namespace std;

template <typename T>
void insertSelectionSort(T arr[],int n){
    //不用考虑第0个元素，因为插入排序初始情况下，第0个元素自身就是有序的
    for(int i=;i<n;i++){
        //寻找arr[i]合适的插入位置
        //每次比较的是当前元素和当前元素的前一个元素的比较，故判断条件是j>0而不是j>=0
        for(int j=i;j>&&arr[j-]>arr[j];j--)
            swap(arr[j],arr[j-]);
    }
}

int main(){
    int a[]={,,,,,,,,,};
    insertSelectionSort(a,);
    for(int i=;i<;i++)
        cout<<a[i]<<" ";
    cout<<endl;

    float b[]={3.3f,2.2f,1.1f};
    insertSelectionSort(b,);
    for(int j=;j<;j++)
        cout<<b[j]<<" ";
    cout<<endl;

    string c[]={"D","C","B","A"};
    insertSelectionSort(c,);
    for(int k=;k<;k++)
        cout<<c[k]<<" ";
    cout<<endl;

    return ;
}

输出结果：

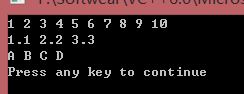
但是，如果我们进行算法性能测试，我们会发现上面的代码并未将这种效率高的优势显示出来。

原因是在这段代码中存在大量的数值交换，而每一次数值交换都包括三次赋值的操作，在本例中还包括访问数组索引所在位置的时间，这些是比简单的比较耗时更多的存在。

所以我们可以对上面关键代码进行优化。

---

template <typename T>
void insertSelectionSort(T arr[],int n){

    for(int i=;i<n;i++){
        //将待排序的关键字复制出来，拿它与它前面的元素进行比较
        T e=arr[i];
        //需要把j的定义拿到for循环的外面，因为最后要在索引j指定的位置（比较后的目标位置）插入复制出来的关键字e
        int j;
        for(j=i;j>&&arr[j-]>e;j--)
            //将比待排序关键字的大的关键字依次后移
            arr[j]=arr[j-];

        arr[j]=e;
    }
}

在这里我们不再调用swap函数进行数值的交换，而是全都是用赋值语句完成相应的操作。

就大大优化了算法。

需要说明一下的是：对于直接插入排序，一趟排序后并不能确保一个关键字到达其最终位置。