洛谷P2150 寿司晚宴
解：发现每个质数只能属于一个人，于是想到每个质数有三种情况：属于a，属于b，都不属于。
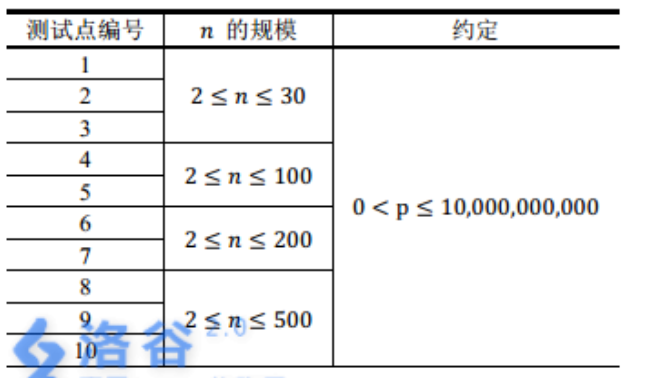
然后考虑状压每个人的质数集合，可以得到30分。
转移就是外层枚举每个数，内层枚举每个人的状态，然后看能否转移。能转移就转移。
考虑优化：有个套路是大于√的质数最多只有一个。于是单独考虑那些，先把不含那些的转移出来放到数组f中。
然后每次外层枚举一个质数，中层枚举它的倍数，内层枚举两个人的状态。
每个质数可以属于a或者属于b或者都不属于。考虑到转移属于a的时候我们不可避免的会算到都不属于(除非再开一维记录)，于是容斥一波。
属于a和属于b因为要分开转移多次(中层枚举倍数)，于是用g，h数组分别转移。
最后f = g + h - f(容斥掉都不属于)。
其实感觉多开一维好想一点......。
#include <bits/stdc++.h> typedef long long LL;
const int N = , M = ; int n, sta[N], p[N], top, last[N], id[N], stk[N], tp;
LL f[][M][M], g[][M][M], MO, h[][M][M], F[M][M];
bool vis[N]; inline void Add(LL &a, const LL &b) {
a += b;
while(a >= MO) a -= MO;
while(a < ) a += MO;
return;
} inline void getp(int n) {
for(int i = ; i <= n; i++) {
if(!vis[i]) {
p[++top] = i;
id[i] = top;
last[i] = i;
}
for(int j = ; j <= top && i * p[j] <= n; j++) {
vis[i * p[j]] = ;
last[i * p[j]] = p[j];
if(i % p[j] == ) break;
}
}
return;
} int main() { //freopen("in.in", "r", stdin); scanf("%d%lld", &n, &MO);
getp(n); int m = ;
while(m < top && p[m + ] <= ) m++;
int lm = << m; for(int i = ; i <= n; i++) {
int x = i, y;
while(x > ) {
y = last[x];
if(id[y] <= m) sta[i] |= ( << (id[y] - ));
else sta[i] |= ( << m);
while(x % y == ) x /= y;
}
} LL ans = ;
f[][][] = ;
for(int i = ; i <= n; i++) {
memset(f[(i + ) & ], , sizeof(f[]));
if((sta[i] & (lm - )) != sta[i]) {
stk[++tp] = i;
memcpy(f[(i + ) & ], f[i & ], sizeof(f[i & ]));
continue;
}
for(int s = ; s < lm; s++) {
for(int t = ; t < lm; t++) {
if((s & t) || (!f[i & ][s][t])) continue;
/// f[i][s][t]
Add(f[(i + ) & ][s][t], f[i & ][s][t]);
if((sta[i] & t) == ) {
Add(f[(i + ) & ][s | sta[i]][t], f[i & ][s][t]);
}
if((sta[i] & s) == ) {
Add(f[(i + ) & ][s][t | sta[i]], f[i & ][s][t]);
}
}
}
} for(int s = ; s < lm; s++) {
for(int t = ; t < lm; t++) {
if(s & t) continue;
Add(F[s][t], f[(n + ) & ][s][t]);
}
} for(int i = ; i <= tp; i++) {
if(vis[stk[i]]) {
continue;
} memcpy(g[], F, sizeof(F));
memcpy(h[], F, sizeof(F));
int time = ;
for(int x = stk[i]; x <= n; x += stk[i], time++) {
memset(g[(time + ) & ], , sizeof(g[]));
memset(h[(time + ) & ], , sizeof(h[])); for(int s = ; s < lm; s++) {
for(int t = ; t < lm; t++) {
if(s & t) continue;
Add(g[(time + ) & ][s][t], g[time & ][s][t]);
Add(h[(time + ) & ][s][t], h[time & ][s][t]);
if((sta[time] & t) == ) {
Add(g[(time + ) & ][s | sta[time]][t], g[time & ][s][t]);
}
if((sta[time] & s) == ) {
Add(h[(time + ) & ][s][t | sta[time]], h[time & ][s][t]);
}
}
}
}
for(int s = ; s < lm; s++) {
for(int t = ; t < lm; t++) {
if(s & t) continue;
F[s][t] = -F[s][t];
Add(F[s][t], g[time & ][s][t]);
Add(F[s][t], h[time & ][s][t]);
}
}
} for(int s = ; s < lm; s++) {
for(int t = ; t < lm; t++) {
if(s & t) continue;
Add(ans, F[s][t]);
}
} printf("%lld\n", ans);
return ;
}
AC代码(容斥)
#include <bits/stdc++.h> typedef long long LL;
const int N = , M = ; int n, sta[N], p[N], top, last[N], id[N], stk[N], tp;
LL f[][M][M], g[][M][M][], MO, h[][M][M][], F[M][M];
bool vis[N]; inline void Add(LL &a, const LL &b) {
a += b;
while(a >= MO) a -= MO;
while(a < ) a += MO;
return;
} inline void getp(int n) {
for(int i = ; i <= n; i++) {
if(!vis[i]) {
p[++top] = i;
id[i] = top;
last[i] = i;
}
for(int j = ; j <= top && i * p[j] <= n; j++) {
vis[i * p[j]] = ;
last[i * p[j]] = p[j];
if(i % p[j] == ) break;
}
}
return;
} int main() { //freopen("in.in", "r", stdin); scanf("%d%lld", &n, &MO);
getp(n); int m = ;
while(m < top && p[m + ] <= ) m++;
int lm = << m; for(int i = ; i <= n; i++) {
int x = i, y;
while(x > ) {
y = last[x];
if(id[y] <= m) sta[i] |= ( << (id[y] - ));
else sta[i] |= ( << m);
while(x % y == ) x /= y;
}
} LL ans = ;
f[][][] = ;
for(int i = ; i <= n; i++) {
memset(f[(i + ) & ], , sizeof(f[]));
if((sta[i] & (lm - )) != sta[i]) {
stk[++tp] = i;
memcpy(f[(i + ) & ], f[i & ], sizeof(f[i & ]));
continue;
}
for(int s = ; s < lm; s++) {
for(int t = ; t < lm; t++) {
if((s & t) || (!f[i & ][s][t])) continue;
/// f[i][s][t]
Add(f[(i + ) & ][s][t], f[i & ][s][t]);
if((sta[i] & t) == ) {
Add(f[(i + ) & ][s | sta[i]][t], f[i & ][s][t]);
}
if((sta[i] & s) == ) {
Add(f[(i + ) & ][s][t | sta[i]], f[i & ][s][t]);
}
}
}
} for(int s = ; s < lm; s++) {
for(int t = ; t < lm; t++) {
if(s & t) continue;
Add(F[s][t], f[(n + ) & ][s][t]);
}
} for(int i = ; i <= tp; i++) {
if(vis[stk[i]]) {
continue;
} //memcpy(g[1], F, sizeof(F));
//memcpy(h[1], F, sizeof(F));
for(int s = ; s < lm; s++) {
for(int t = ; t < lm; t++) {
g[][s][t][] = F[s][t];
g[][s][t][] = ;
h[][s][t][] = F[s][t];
h[][s][t][] = ;
}
} int time = ;
for(int x = stk[i]; x <= n; x += stk[i], time++) {
memset(g[(time + ) & ], , sizeof(g[]));
memset(h[(time + ) & ], , sizeof(h[])); for(int s = ; s < lm; s++) {
for(int t = ; t < lm; t++) {
if(s & t) continue;
Add(g[(time + ) & ][s][t][], g[time & ][s][t][]);
Add(g[(time + ) & ][s][t][], g[time & ][s][t][]);
Add(h[(time + ) & ][s][t][], h[time & ][s][t][]);
Add(h[(time + ) & ][s][t][], h[time & ][s][t][]);
if((sta[time] & t) == ) {
Add(g[(time + ) & ][s | sta[time]][t][], g[time & ][s][t][]);
Add(g[(time + ) & ][s | sta[time]][t][], g[time & ][s][t][]);
}
if((sta[time] & s) == ) {
Add(h[(time + ) & ][s][t | sta[time]][], h[time & ][s][t][]);
Add(h[(time + ) & ][s][t | sta[time]][], h[time & ][s][t][]);
}
}
}
}
for(int s = ; s < lm; s++) {
for(int t = ; t < lm; t++) {
if(s & t) continue;
//F[s][t] = -F[s][t];
//F[s][t] = 0;
Add(F[s][t], g[time & ][s][t][]);
Add(F[s][t], h[time & ][s][t][]);
}
}
} for(int s = ; s < lm; s++) {
for(int t = ; t < lm; t++) {
if(s & t) continue;
Add(ans, F[s][t]);
}
} printf("%lld\n", ans);
return ;
}
AC代码(多开一维)
洛谷P2150 寿司晚宴的更多相关文章
- 洛谷$P2150\ [NOI2015]$寿司晚宴 $dp$
正解:$dp$ 解题报告: 传送门$QwQ$. 遇事不决写$dp$($bushi$.讲道理这题一看就感觉除了$dp$也没啥很好的算法能做了,于是考虑$dp$呗 先看部分分?$30pts$发现质因数个数 ...
- UOJ #129 / BZOJ 4197 / 洛谷 P2150 - [NOI2015]寿司晚宴 （状压dp+数论+容斥）
题面传送门 题意: 你有一个集合 \(S={2,3,\dots,n}\) 你要选择两个集合 \(A\) 和 \(B\),满足: \(A \subseteq S\),\(B \subseteq S\), ...
- 【Luogu】P2150寿司晚宴（状压DP）
题目链接 反正……我是没什么想法了,全程看题解 (或者说自己想了半天错解) 因为大于根n的质数最多只会在一个数里出现一种,所以可以把数拆成两部分:小数的二进制集合和大数. 然后把大数一样的放到一起DP ...
- BZO4197 & 洛谷2150 & UOJ129：[NOI2015]寿司晚宴——题解
https://www.lydsy.com/JudgeOnline/problem.php?id=4197 https://www.luogu.org/problemnew/show/P2150 ht ...
- 【洛谷P3749】[六省联考2017]寿司餐厅（网络流）
洛谷 题意: 给出\(n\)份寿司,现可以选取任意多次连续区间内的寿司,对于区间\([l,r]\),那么贡献为\(\sum_{i=l}^r \sum_{j=i}^rd_{i,j}\)(对于相同的\(d ...
- 【BZOJ-4197】寿司晚宴 状压DP
4197: [Noi2015]寿司晚宴 Time Limit: 10 Sec Memory Limit: 512 MBSubmit: 694 Solved: 440[Submit][Status] ...
- 洛谷1640 bzoj1854游戏 匈牙利就是又短又快
bzoj炸了,靠离线版题目做了两道(过过样例什么的还是轻松的)但是交不了,正巧洛谷有个"大牛分站",就转回洛谷做题了 水题先行,一道傻逼匈牙利 其实本来的思路是搜索然后发现写出来类 ...
- [BZOJ4197][Noi2015]寿司晚宴
4197: [Noi2015]寿司晚宴 Time Limit: 10 Sec Memory Limit: 512 MBSubmit: 412 Solved: 279[Submit][Status] ...
- 洛谷P1352 codevs1380 没有上司的舞会——S.B.S.
没有上司的舞会 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 钻石 Diamond 题目描述 Description Ural大学有N个职员,编号为1~N.他们有 ...
随机推荐
- js 判断字符串中是否包含某个字符串的方法实例
String对象的方法 方法一: indexOf() (推荐) var str = "123"; console.log(str.indexOf("3") ...
- Laravel数据库操作的三种方式
http://blog.csdn.net/zls986992484/article/details/52824962
- RabbitMQ在Ubuntu 16.04下的安装与配置
安装执行如下命令: echo 'deb http://www.rabbitmq.com/debian/ testing main' | sudo tee /etc/apt/sources.list.d ...
- case when 空值判断
在对数据库进行查询时,遇到了一个问题:查询结果中的某一列需要判断另一列是否为空的来确定值,自然就想到了case when,于是写出了下面的SQL(其他部分省略): (case date when nu ...
- LODOP 获取打印设计代码不带INIT初始化语句
前面的博文生成JS代码模版和文档式模版,生成的是带初始化语句的模版,如果想要打印多个,可以循环多个任务,什么是一个任务,可查看本博客相关博文:Lodop打印语句最基本结构介绍(什么是一个任务)一个任务 ...
- Scss - 简单笔记
原文链接:scss 教程 手头上疯狂在用 scss,虽然可以在里面写原生的 css, 但是为了保持风格的一致性,还是滚去看了看 scss 文档. 一.变量 变量的引入是 scss 的一个核心特性,变量 ...
- 1.rabbitmq高可用方案
采用标准集群模式 HAPROXY + rabbitmq 2个 ram 和 一个 disk 节点 主机规划: 192.168.157.128 haproxy keepalive 主 ram节点 1 ...
- git 强制推送
Git 强制推送方法(一般不建议使用) $ git push -u origin master -f
- xshell使用rz/sz完成文件上传下载
yum -y install lrzsz 安装lrzsz 使用rz完成文件上传 使用sz完成文件下载
- Linux(Centos)下调整分区大小（以home和根分区为例）
在安装新系统的时候,有时候没法预估或者说错误的划分了分区大小,常常会导致我们后面的操作出现极大地不方便,比如某个分区分的太小了,导致 软件安装的时候会报安装空间不够,这就很麻烦.在这里我就记录一下 ...