MT【270】含参绝对值函数最大之二
已知$f(x)=2ax\cos^2x+(a-1)\cos x-1,a>0$,记$|f(x)|$的最大值为$A$,
1)求A.
2)证明:$|-2a\sin 2x+(1-a)\sin x|\le 2A$

分析:(1)

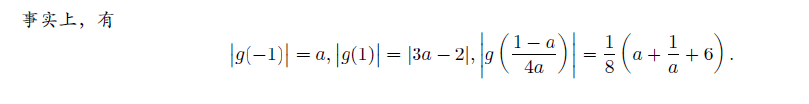
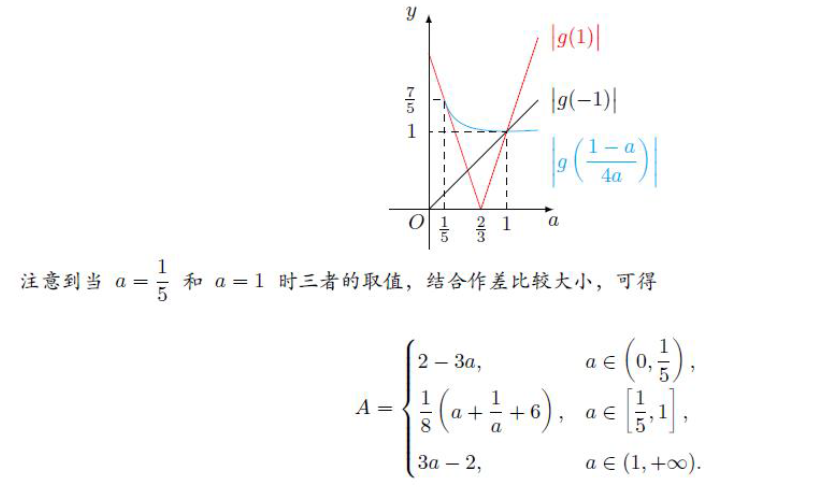
(2)

注:第一题做法一般是分类讨论,这里通过图像可以化简计算,老实讨论可以参考这题
MT【270】含参绝对值函数最大之二的更多相关文章
- MT【289】含参绝对值的最大值之三
已知$a>0$,函数$f(x)=e^x+3ax^2-2e x-a+1$,(1)若$f(x)$在$[0,1]$上单调递减,求$a$的取值范围.(2)$|f(x)|\le1$对任意$x\in[0,1 ...
- Java 解惑:Random 种子的作用、含参与不含参构造函数区别
Random 通常用来作为随机数生成器,它有两个构造方法: Random random = new Random(); Random random2 = new Random(50); 1.不含参构造 ...
- Java Random 含参与不含参构造函数的区别
##Random 通常用来作为随机数生成器,它有两个构造方法: Random random = new Random(); Random random2 = new Random(50); 1.不含参 ...
- MT【269】含参函数绝对值最大
设函数$f(x)=ax^2+(2b+1)x-a-2$($a,b\in\mathcal R$,$a\neq 0$). (1) 若$a=-2$,求函数$y=|f(x)|$在$[0,1]$上的最大值$M(b ...
- Python学习之高阶函数--嵌套函数、函数装饰器、含参函数装饰器
玩了一晚上王者,突然觉得该学习,然后大晚上的搞出来这道练习题,凌晨一点写博客(之所以这么晚就赶忙写是因为怕第二天看自己程序都忘了咋写的了),我太难了o(╥﹏╥)o 言归正传,练习题要求:构造类似京东的 ...
- iOS,object-c传参c语言的二维数组
有那么一瞬间,懒得用NSArray,NSNumber,NSValue等一大堆蛋疼的转换,所以就定义了一个C的二维数组,反正OC支持C混编,可是蛋疼往往是传递的,这里不疼了,哪里就要疼,想把一个c的二维 ...
- MT【9】绝对值二次函数
解答: 评:容易用绝对值不等式证明当$x\in[1,5]$时$|x^2+px+q|\ge2$
- [leetcode]270. Closest Binary Search Tree Value二叉搜索树中找target的最接近值
Given a non-empty binary search tree and a target value, find the value in the BST that is closest t ...
- 270. Closest Binary Search Tree Value 二叉搜索树中,距离目标值最近的节点
[抄题]: Given a non-empty binary search tree and a target value, find the value in the BST that is clo ...
随机推荐
- 反射reflect
JAVA反射机制是在运行状态中,对于任意一个类,都能够知道这个类的所有属性和方法:对于任意一个对象,都能够调用它的任意方法和属性:这种动态获取信息以及动态调用对象方法的功能称为java语言的反射机制. ...
- p151开映射札记
1. 如何理解这句话? 2.连续有什么用? 3.为什么区间包含,经过算子T还是包含? 谢谢 谢谢学长 我懂了 1.2. 3有点儿模糊 1.连续等价于开集原像是开集,而可逆算子的逆的原像就是的 ...
- semantic-ui 输入框
1.标准输入框 semantic-ui中定义输入框需要将input标签包含于另外一个标签内,外层标签的class为ui input,注意外层标签可以是div,span.p.i. <div cla ...
- Ubuntu16系统中安装htpasswd
htpasswd是Apache附带的程序, htpasswd生成包含用户名和密码的文本文件, 每行内容格式为“用户名:密码”, 用于用户文件的基本身份认证. 当用户浏览某些网页的时候, 浏览器会提示输 ...
- Jquery模拟多选框(checkbox)
代码如下: <!DOCTYPE html> <html> <head> <meta charset="utf-8"> <tit ...
- VMWARE中NAT下获取不到IP
1.编辑-虚拟网络编辑器-dhcp设置 2.虚拟机-可移动设备-网络适配器-设置,注意:这里一定要选nat,当初我就是选了桥接,死活上不去,搞了2个小时.
- memcach 命令行
1. cmd上登录memcache # telnet 127.0.0.1 11211 2. 列出所有items stats items 3. 通过itemid获取key 接下来基于列出的i ...
- ERP行业内幕看了这五个问题全懂了
ERP系统是现代企业实现信息化管理的必经之路.但很多管理人员或已经在用ERP的人员,其实并不太懂ERP系统是什么意思,有哪些好处等,导致实际使用过程中经常大材小用,或者“英雄无用武之地”.所以,为了更 ...
- thymeleaf 简易使用范例
thymeleaf 范例: <!DOCTYPE html> <html lang="en" xmlns:th="http://www.w3.org/19 ...
- 五、同一台MySQL服务器启动多个端口-为读写分离做准备
一.安装数据库 https://www.cnblogs.com/huiyi0521/p/10113280.html 二.使用 mysql 命令为 root 用户授权 mysql 远程连接服务 mysq ...
