<数据结构与算法分析>读书笔记--数学知识复习

数学知识复习是《数据结构与算法分析》的第一章引论的第二小节，之所以放在后面，是因为我对数学确实有些恐惧感。不过再怎么恐惧也是要面对的。

一、指数

基本公式:

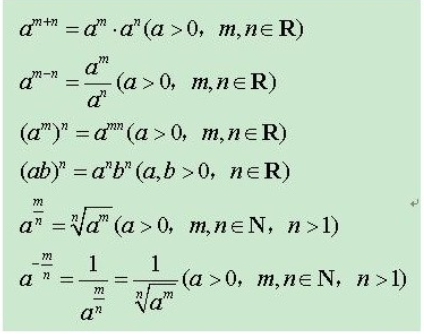
二、对数

在计算机科学中除非有特别的声明，否则所有的对数都是以2为底的。

定义:X^A=B 当且仅当logxB=A。

由该定义可以推出几个方便的等式。

定理1:

logaB=logcB/logcA; A，B，C>0，A不等于1

定理2:

logAB=logA+logB；A，B大于0

三、级数

最容易记忆的公式:

四、模运算

如果N整除A-B，那么就说A与B模N同余，记为A===B（mod N）。直观地看，这意味着无论是A还是B被N去除，所得余数都是相同的。于是，81===61====1(mod 10)。如同等号的情况一样，若A===B(mod N)，则A+C====B+C（mode N）以及AD===BD（mod N）

五、证明方法

证明数据结构分析中的结论的两种最常用的方法是归纳法证明和反证法证明。证明一个定理不成立的最好的方法是举出一个反例。

1.归纳法证明

由归纳法进行的证明有两个标准的部分。第一步是证明基准情形，就是确定定理对某个小的值的正确性；这一步总是很简单。接着，进行归纳假设。一般说来，它指的是假设定理对直到某个有限数k的所有的情况都是成立的。然后使用这个假设证明定理对下一个值(通常是k+1)也是成立的。至此定理得证(在k是有限的情形下)。

2.反证法证明

反证法证明是通过假设定理不成立，然后证明该假设导致某个已知的性质不成立，从而原假设是错误的。一个经典的例子是证明存在无穷多个素数。为了证明这个结论，我们假设定理不成立。于是，存在某个最大的素数Pk。令P1，P2，....，Pk是依序排列的所有素数并考虑:

N=P1P2P3..Pk+1

显然，N是比Pk大的数，根据假设N不是素数。可是，P1，P2，....,Pk都不能整除N，因为除得的结果总有余数1.这就产生一个矛盾，因为每个整数或者是素数，或者是素数的乘积。

因此，Pk是最大素数的原假设是不成立的，这正意味着定理成立。

未完待续，接下来我要看相关的学习视频，接下来会有补充的。