洛谷【P2458】[SDOI2006]保安站岗 题解 树上DP

题目描述

五一来临，某地下超市为了便于疏通和指挥密集的人员和车辆，以免造成超市内的混乱和拥挤，准备临时从外单位调用部分保安来维持交通秩序。

已知整个地下超市的所有通道呈一棵树的形状；某些通道之间可以互相望见。总经理要求所有通道的每个端点（树的顶点）都要有人全天候看守，在不同的通道端点安排保安所需的费用不同。

一个保安一旦站在某个通道的其中一个端点，那么他除了能看守住他所站的那个端点，也能看到这个通道的另一个端点，所以一个保安可能同时能看守住多个端点（树的结点），因此没有必要在每个通道的端点都安排保安。

编程任务：

请你帮助超市经理策划安排，在能看守全部通道端点的前提下，使得花费的经费最少。

输入输出格式

输入：

第\(1\)行 \(n\)，表示树中结点的数目。

第\(2\)行至第\(n+1\)行，每行描述每个通道端点的信息，依次为：该结点标号\(i（0<i<=n）\)，在该结点安置保安所需的经费\(k（<=10000）\)，该边的儿子数\(m\)，接下来\(m\)个数，分别是这个节点的\(m\)个儿子的标号\(r1，r2，...，rm\)。

对于一个\(n（0 < n <= 1500）\)个结点的树，结点标号在\(1\)到\(n\)之间，且标号不重复。

输出:

最少的经费。

如右图的输入数据示例

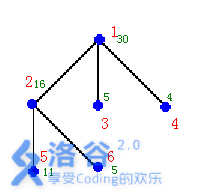
输入输出样例

输入样例#1：

6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

输出样例#1：

25

说明

样例说明：在结点\(2，3，4\)安置\(3\)个保安能看守所有的\(6\)个结点，需要的经费最小：\(25\)

---

根据题目描述很容易想到是树上\(DP\)，但是有很多需要考虑到的东西：

首先容易被坑的一点：

• 很可能会直接想到两种状态：当前点占用和不占用。
• 在这种情况下会很容易就作出如下的判断
  • \(F[u][1]+=min\{F[v][0],F[v][1]\};\)（当前点占用的转移）
  • \(F[u][0]+=F[v][1];\)（当前点不占用的转移）

然后就会第一时间\(w\)\(\bar a\)掉这个题目。

为什么呢？因为这个转移中，我们忽略了子节点对父节点的影响，子节点的选中也可以控制父节点，所以我们的状态应该有三个：

• 当前点被占用（子节点选啥都可以，直接取最小值）
• 当前点没有被占用（父节点占用并控制该点，所以可以把子节点里面已经独立可用的都挖过来）
• 当前点没有被占用，但是子节点中存在有已经被占用的点
  • 这个转移相对不是很好考虑，怎么确认子节点中谁被占用呢？
  • 我们先考虑不管子节点有没有被占用的，直接先取两种转移状态最小值临时存起来
  • 然后一一比较，看哪一个子节点变成占用态消耗最少，答案取min
  • 复杂度\(O(n)\)

实际上算是树上\(DP\)的一种常用套路吧，不过本蒻以前没有掌握，被这个题目好好教育了一下。

Code：

#include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 1510
#define INF 0x3f3f3f3f
using namespace std;
int cnt,head[MAXN],deep[MAXN];
int n,vis[MAXN],arr[MAXN],size[MAXN],f[MAXN][4];
struct edge{
	int nxt;
	int to;
}e[MAXN<<1];
void dfs(int u,int fa){
	f[u][1]=arr[u];//预先处理被占用的情况
	int sum=0;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v!=fa){
			//对子树的处理
			dfs(v,u);
			f[u][1]+=min(f[v][1],min(f[v][2],f[v][3]));
			sum+=min(f[v][1],f[v][2]);
		}
	}
	f[u][3]=sum,f[u][2]=INF;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v!=fa){
			f[u][2]=min(f[u][2],sum-min(f[v][1],f[v][2])+f[v][1]);
		}
	}
//	printf("f[%d][1]=%d f[%d][2]=%d f[%d][3]=%d\n",u,f[u][1],u,f[u][2],u,f[u][3]);
	return;
}

inline void add(int from,int to){
	e[++cnt].nxt=head[from];
	e[cnt].to=to;
	head[from]=cnt;
}

int main(){
	int u,v,m;
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		scanf("%d",&u);
		scanf("%d%d",&arr[u],&m);
		for(int j=1;j<=m;++j){
			scanf("%d",&v);
			add(u,v);
			add(v,u);
		}
	}//arr记录价格
	//f[i][1]->本节点占用时子树最小花费
	//f[i][2]->本节点不占用但被控制时子树最小花费
	//f[i][3]->本节点完全不受控制时子树最小花费
	dfs(1,0);
//	for(int i=1;i<=n;++i){
//		printf("size %d = %d\n",i,size[i]);
//	}
//	size保存子树大小
	printf("%d\n",min(f[1][1],f[1][2]));
	return 0;
}