《Unity3D 实战核心技术详解》书中关于矩阵的错误

最近一直在学习实时渲染，不免要接触线性代数。而渲染中，一定会用到矩阵，当我再次去复习我之前看的书时，发现《Unity3D 实战核心技术详解》关于矩阵就有几处错误 ，特标注出来。

书的第一章《3D数学与Unity》，1.3.2讲矩阵缩放、1.3.3讲矩阵的旋转。缩放是一个矩阵，后面旋转针对绕三个不同的轴的旋转矩阵（x、y、z），总共4个矩阵，其中3个是错误的，只有一个绕y轴旋转是正确的。我不确定是印刷问题，还是作者本身对矩阵了解和掌握的就不深入，但出现这样的低级错误实属不该。

我直接上图片，不然口说无凭。

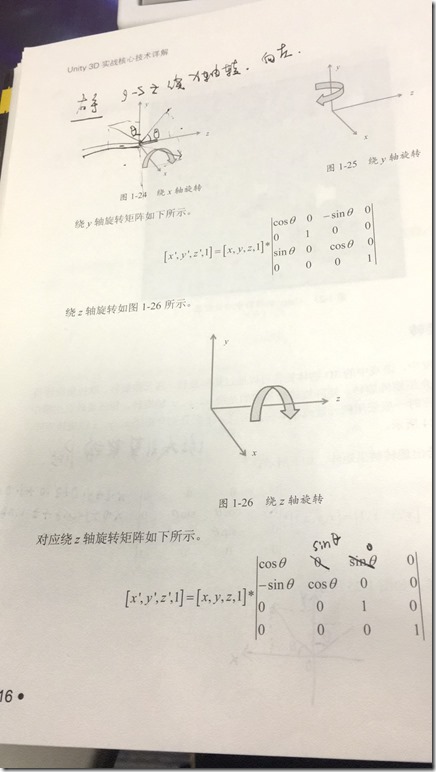
如第一张图所示，如果缩放的矩阵如书中所注，那么x’= x·Sx + y 而不是期望的 x.Sx，同理绕x轴旋转，那么x轴的坐标应当是不动的，也就是除了第一列的第一个为1外，其余应该为0，而第二行居然出现了1，那x’= x + y了，这根本就不是旋转了啊 ，绕z轴旋转的就更离谱了…

好了，矩阵确实麻烦，但它却是理解和学习3D必不可少的知识。如果判断一个矩阵是否正确呢？这里我推荐《程序员的数学3 —— 线性代数》这本书中的一个方法，如下图所示。

注意看画线的部分，我正是掌握了书中这个简单的方法，再去看有“错误”的那本书的矩阵时，一眼就发现矩阵是错的。希望这个小技巧和方法能帮助到你：

将输入的列向量放倒，然后将对应的元素分别相乘。

再额外补充一句，我之前也看孟岩在CSDN上写的那三篇《理解矩阵》，里面提及的书有：

《数学：它的内容、方法和意义》

《线性代数五讲》

《数学概观》

《数学拾遗》

《重温微积分》

《计算机图形学 —— 几何工具算法详解》

因为作者非数学系的专业人士，所以它的描述可能存在不准确的地方，但那是他自己的理解，能帮助到不理解矩阵的人，我觉得也是很有价值的。毕竟大部分人只是需要了解矩阵到底是什么东东，好奇为什么要用矩阵呢，至于矩阵更深层次的研究可能就不是那么在意了。科普有科普的作用，专业有专业的必要。

其实我觉得关于矩阵，看维基百科上的定义已经写的很清晰、明了了，仔细研究透，也就有个大概的了解了。链接地址  https://zh.wikipedia.org/wiki/矩阵 

那矩阵到底是什么，以我目前的理解和认知，矩阵就是映射，矩阵就是映射，矩阵就是映射（重要的事情说三遍！）。

这里推荐几个我觉得非常好的视频给大家，更直观，进一步降低学习门槛。

【官方双语/合集】线性代数的本质 - 系列合集（用直观的动画、简洁的语言来讲述线性代码，你值得观看！）

https://www.bilibili.com/video/av6731067/index_1.html

麻省理工公开课：线性代数
http://open.163.com/special/opencourse/daishu.html

Introduction to Linear Algebra, Fifth Edition（2016） —— 线性代数教程评价最高的书，没有之一
http://math.mit.edu/~gs/linearalgebra/

Linear Algebra Done Wrong （Sergei Treil）
https://www.math.brown.edu/~treil/papers/LADW/LADW.html

陶哲轩在UCLA的linear algebra讲义 （通过阮一峰的博客了解到，他是40岁以下最聪明的美国科学家，24岁便被聘为正教授）
http://www.math.ucla.edu/~tao/resource/general/115a.3.02f/

最后扯点题外话，买书尽量买豆瓣上评价高的或者官方出品的（有口碑和品质保障），不然反而被误导了，读书有风险，吸收需谨慎（也可以说尽信书不如无书）。

这里我推荐一本书：《游戏引擎架构》，写书的作者本身的品质有保障，译者的水平也是杠杠的。

虽然我指出书中关于矩阵部分的三个错误（点积那部分不知道是印刷错误还是什么原因，存在错误），但本书其它章节依旧值得去阅读，给出的代码也并不算复杂，毕竟作者长期奋战在一线，网上也有很多他录制的视频。更多是吸收他实战的经验，理论部分我建议泛泛看一看，再找本更专业（评价更高）的书去查阅，这本书的理论写的并不好。