DCT变换、DCT反变换、分块DCT变换

一、引言

DCT变换的全称是离散余弦变换(Discrete Cosine Transform)，主要用于将数据或图像的压缩，能够将空域的信号转换到频域上，具有良好的去相关性的性能。DCT变换本身是无损的，但是在图像编码等领域给接下来的量化、哈弗曼编码等创造了很好的条件，同时，由于DCT变换时对称的，所以，我们可以在量化编码后利用DCT反变换，在接收端恢复原始的图像信息。DCT变换在当前的图像分析已经压缩领域有着极为广大的用途，我们常见的JPEG静态图像编码以及MJPEG、MPEG动态编码等标准中都使用了DCT变换。

---

二、一维DCT变换

一维DCT变换时二维DCT变换的基础，所以我们先来讨论下一维DCT变换。一维DCT变换共有8种形式，其中最常用的是第二种形式，由于其运算简单、适用范围广。我们在这里只讨论这种形式，其表达式如下：

其中，f(i)为原始的信号，F(u)是DCT变换后的系数，N为原始信号的点数，c(u)可以认为是一个补偿系数，可以使DCT变换矩阵为正交矩阵。

---

三、二维DCT变换

二维DCT变换其实是在一维DCT变换的基础上在做了一次DCT变换，其公式如下：

由公式我们可以看出，上面只讨论了二维图像数据为方阵的情况，在实际应用中，如果不是方阵的数据一般都是补齐之后再做变换的，重构之后可以去掉补齐的部分，得到原始的图像信息，这个尝试一下，应该比较容易理解。

另外，由于DCT变换高度的对称性，在使用Matlab进行相关的运算时，我们可以使用更简单的矩阵处理方式：

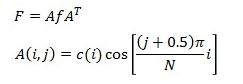
接下来利用Matlab对这个过程进行仿真处理：

 1 clear;
 2 clc;
 3 X=round(rand(4)*100)   %产生随机矩阵
 4 A=zeros(4);
 5 for i=0:3
 6     for j=0:3
 7         if i==0
 8             a=sqrt(1/4);
 9         else
10             a=sqrt(2/4);
11         end
12         A(i+1,j+1)=a*cos(pi*(j+0.5)*i/4);
13     end
14 end
15 Y=A*X*A'        %DCT变换
16 YY=dct2(X)      %Matlab自带的dct变换

运行结果为：

 1 X =
 2
 3     42    66    68    66
 4     92     4    76    17
 5     79    85    74    71
 6     96    93    39     3
 7
 8
 9 Y =
10
11   242.7500   48.4317   -9.7500   23.5052
12   -12.6428  -54.0659    7.4278   22.7950
13    -6.2500   10.7158  -19.7500  -38.8046
14    40.6852  -38.7050  -11.4653  -45.9341
15
16
17 YY =
18
19   242.7500   48.4317   -9.7500   23.5052
20   -12.6428  -54.0659    7.4278   22.7950
21    -6.2500   10.7158  -19.7500  -38.8046
22    40.6852  -38.7050  -11.4653  -45.9341

由上面的结果我们可以看出，我们采用的公式的方法和Matlab自带的dct变化方法结果是一致的，所以验证了我们方法的正确性。

如果原始信号是图像等相关性较大的数据的时候，我们可以发现在变换之后，系数较大的集中在左上角，而右下角的几乎都是0，其中左上角的是低频分量，右下角的是高频分量，低频系数体现的是图像中目标的轮廓和灰度分布特性，高频系数体现的是目标形状的细节信息。DCT变换之后，能量主要集中在低频分量处，这也是DCT变换去相关性的一个体现。

之后在量化和编码阶段，我们可以采用“Z”字形编码，这样就可以得到大量的连续的0，这大大简化了编码的过程。

---

四、二维DCT反变换

在图像的接收端，根据DCT变化的可逆性，我们可以通过DCT反变换恢复出原始的图像信息，其公式如下：

同样的道理，我们利用之前的矩阵运算公司可以推导出DCT反变换相应的矩阵形式：

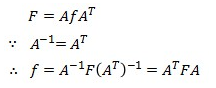
下面我们用Matlab对这个过程进行仿真：

 1 clear;
 2 clc;
 3 X=[
 4     61    19    50    20
 5     82    26    61    45
 6     89    90    82    43
 7     93    59    53    97] %原始的数据
 8 A=zeros(4);
 9 for i=0:3
10     for j=0:3
11         if i==0
12             a=sqrt(1/4);
13         else
14             a=sqrt(2/4);
15         end
16         A(i+1,j+1)=a*cos(pi*(j+0.5)*i/4); %生成变换矩阵
17     end
18 end
19 Y=A*X*A'   %DCT变换后的矩阵
20 X1=A'*Y*A  %DCT反变换恢复的矩阵

运行结果为：

 1 X =
 2
 3     61    19    50    20
 4     82    26    61    45
 5     89    90    82    43
 6     93    59    53    97
 7
 8
 9 Y =
10
11   242.5000   32.1613   22.5000   33.2212
12   -61.8263    7.9246  -10.7344   30.6881
13   -16.5000  -14.7549   22.5000   -6.8770
14     8.8322   16.6881  -35.0610   -6.9246
15
16
17 X1 =
18
19    61.0000   19.0000   50.0000   20.0000
20    82.0000   26.0000   61.0000   45.0000
21    89.0000   90.0000   82.0000   43.0000
22    93.0000   59.0000   53.0000   97.0000

我们可以看到反变换后无损的恢复了原始信息，所以证明了方法的正确性。但是在实际过程中，需要量化编码或者直接舍弃高频分量等处理，所以会出现一定程度的误差，这个是不可避免的。

---

五、分块DCT变换

在实际的图像处理中，DCT变换的复杂度其实是比较高的，所以通常的做法是，将图像进行分块，然后在每一块中对图像进行DCT变换和反变换，在合并分块，从而提升变换的效率。具体的分块过程中，随着子块的变大，算法复杂度急速上升，但是采用较大的分块会明显减少图像分块效应，所以，这里面需要做一个折中，在通常使用时，大都采用的是8*8的分块。

Matlab的 blkproc 函数可以帮我们很方便的进行分块处理，下面给出我们的处理过程：

 1 clear;
 2 clc;
 3
 4 X=imread('pepper.bmp');
 5 X=double(X);
 6 [a,b]=size(X);
 7 Y=blkproc(X,[8 8],'dct2');
 8 X1=blkproc(Y,[8 8],'idct2');
 9
10 figure
11 subplot(1,3,1);
12 imshow(uint8(X));
13 title('原始图');
14
15 subplot(1,3,2);
16 imshow(uint8(Y));
17 title('分块DCT变换图');
18
19 subplot(1,3,3);
20 imshow(uint8(X1));
21 title('分块DCT恢复图');
22
23 Y1=dct2(X);
24 X10=idct2(Y1);
25
26 figure
27 subplot(1,3,1);
28 imshow(uint8(X));
29 title('原始图');
30
31 subplot(1,3,2);
32 imshow(uint8(Y1));
33 title('DCT变换图');
34
35 subplot(1,3,3);
36 imshow(uint8(X10));
37 title('DCT反变换恢复图');

运行结果为：

从图中，我们可以明显看出DCT变换与分块DCT变换在使用时的区别。

---

六、小结

DCT、DWT等是图像处理的基础知识，之前一直有用到，但是没怎么好好整理下，今天在做稀疏编码的时候正好有用到，就顺便整了下，希望能够给后来者一些提示。

转自：https://www.cnblogs.com/lzhen/p/3947600.html