HGOI20180813 (NOIP2018 提高组 Day2 模拟试题)
省常中省选提高Day2 继续

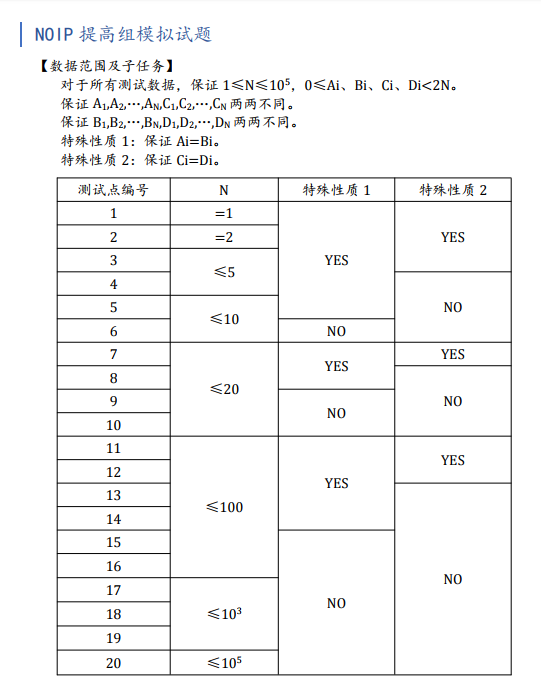
第一题就考了贪心,正解95pts的贪心策略第一印象是想到的,但是被自己否定掉了qwq,然后打了
不是正解的贪心,样例5没过(可怜)思路如下:先找出每个门对应可以通过的人数是多少,每个人能通过多少门逃走
然后枚举能通过门最少的点优先选,合法门里面可以通过这扇门逃走人数最少的一扇门,这样做(57pts)
贴下代码:
# include <bits/stdc++.h>
using namespace std;
const int MAXN=;
struct rec{
int x,y,cnt;
bool flag;
};
rec a[MAXN],b[MAXN];
inline bool cmp(rec a,rec b)
{
if (a.y!=b.y) return a.y<b.y;
else return a.x<b.x;
}
inline bool cmpa(rec a,rec b)
{
if (a.cnt!=b.cnt) return a.cnt>b.cnt;
else if (a.x!=b.x) return a.x<b.x;
else return a.y<b.y;
}
int main()
{
//freopen("guide.in","r",stdin);
// freopen("guide.out","w",stdout);
int num; scanf("%d",&num);
int n; scanf("%d",&n);
for (register int i=;i<=n;i++) {
scanf("%d%d",&a[i].x,&a[i].y);
a[i].x++;a[i].y++;
a[i].cnt=;a[i].flag=true;
}
for (register int i=;i<=n;i++) {
scanf("%d%d",&b[i].x,&b[i].y);
b[i].x++;b[i].y++;
b[i].flag=true;
b[i].cnt=;
}
for (register int i=;i<=n;i++) {
for (register int j=;j<=n;j++)
if (b[j].x>=a[i].x&&b[j].y>=a[i].y) b[j].cnt++,a[i].cnt++;
}
int ans=;
int yy=;
for (register int i=;i<=n;i++) {
int maxx=,minn=INT_MAX,p=-,w;
for (register int j=;j<=n;j++)
if (a[j].flag) {
if (a[j].cnt<=minn) {
minn=a[j].cnt; w=j;
}else if (a[j].cnt==minn&&a[j].x>a[w].x){
minn=a[j].cnt; w=j;
}else if (a[j].cnt==minn&&a[j].x==a[w].x&&a[j].y>a[w].x){
minn=a[j].cnt; w=j;
}
}
a[w].flag=false;
minn=INT_MAX;
for (register int j=;j<=n;j++)
if (b[j].flag&&b[j].x>=a[w].x&&b[j].y>=a[w].x&&b[j].cnt<=minn)
if (b[j].cnt<minn){
p=j; minn=b[j].cnt;
} else if (b[j].x>b[p].x) {
p=j; minn=b[j].cnt;
} else if (b[j].x==b[p].x&&b[j].y>b[p].x) {
p=j; minn=b[j].cnt;
}
if (p==-) continue;
b[p].flag=false; ans++;
for (int j=;j<=n;j++) if (a[j].x<=b[p].x&&a[j].y<=b[p].y) a[j].cnt--;
for (int j=;j<=n;j++) if (b[j].x<=a[w].x&&b[j].y<=a[w].y) b[j].cnt--;
}
printf("%d\n",ans);
return ;
}
正解是什么呢?
其实出奇的简单,从左到右扫每一个门,然后找这个门前面合法的y坐标最小的人。这样可以过95pts。
但是这里开了O2优化所以我们考虑stl优化O(n2)的初始化维护:set
#include<bits/stdc++.h>
using namespace std;
const int MAXN = ;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); }
template <typename T> void read(T &x) {
x = ; int f = ;
char c = getchar();
for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
for (; isdigit(c); c = getchar()) x = x * + c - '';
x *= f;
}
template <typename T> void write(T x) {
if (x < ) x = -x, putchar('-');
if (x > ) write(x / );
putchar(x % + '');
}
template <typename T> void writeln(T x) {
write(x);
puts("");
}
set <int> st;
bool type[MAXN]; int pos[MAXN];
int main() {
freopen("guide.in", "r", stdin);
freopen("guide.out", "w", stdout);
int num; read(num);
int n; read(n);
for (int i = ; i <= n; i++) {
int x, y; read(x), read(y);
type[x] = true, pos[x] = y;//type[x]表示x坐标的这个位置是人(true)还是人(false)
}
for (int i = ; i <= n; i++) {
int x, y; read(x), read(y);
type[x] = false, pos[x] = y;
}
int ans = ;
for (int i = ; i < * n; i++) {
if (type[i]) st.insert(pos[i]);//如果x坐标这个位置是人,那么塞入set(待门来找)
else {
set <int> :: iterator tmp = st.lower_bound(pos[i]);//tmp指向这个门前面下面离这个门最近的人之后的那个位置
if (tmp == st.begin()) continue;//如果没找到就continue
tmp--; ans++; //累加答案
st.erase(tmp);//注意tmp是指这个门前面下面离这个门最近的人之后的那个位置而不是人的位置刚好比人的位置多1,所以tmp--才是指向那个人
}
}
writeln(ans);
return ;
}


看数据范围这道题是dfs,需要注意这样一个性质:
不管怎么换行中的数字是不会发生除了顺序的变化的,那么我们就暴力找出每一次交换,看看个数是否相同,如果相同就是合法
如果不同就是不合法就不对应的,这是可行性剪枝。(首先你要保证每行的个数一样,才能最终判断)
既然暴力判断交换那么就不用记录状态了,直接回溯暴力判断是否是中心对称即可
#include<bits/stdc++.h>
using namespace std;
const int MAXN = ;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); }
template <typename T> void read(T &x) {
x = ; int f = ;
char c = getchar();
for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
for (; isdigit(c); c = getchar()) x = x * + c - '';
x *= f;
}
template <typename T> void write(T x) {
if (x < ) x = -x, putchar('-');
if (x > ) write(x / );
putchar(x % + '');
}
template <typename T> void writeln(T x) {
write(x);
puts("");
}
int n, m;
char mp[MAXN][MAXN];
int rnum[MAXN], cnum[MAXN];
bool visrow[MAXN], viscol[MAXN], solved;
bool row[MAXN][MAXN], col[MAXN][MAXN];
void check() {
for (int i = ; i <= n; i++)
for (int j = ; j <= m; j++)
if (mp[rnum[i]][cnum[j]] != mp[rnum[n - i + ]][cnum[m - j + ]]) return;
printf("YES\n");
solved = true;
}
void workc(int pos, int type) {
if (solved) return;
if (pos == ) {
check();
return;
}
if (type) {
for (int i = ; i <= m; i++) {
viscol[i] = true;
cnum[pos] = i;
workc(pos - , );
viscol[i] = false;
}
} else {
for (int i = ; i <= m; i++) {
if (viscol[i]) continue;
for (int j = i + ; j <= m; j++)
if (!viscol[j] && col[i][j]) {
viscol[i] = true;
viscol[j] = true;
cnum[pos] = i;
cnum[m + - pos] = j;
workc(pos - , );
viscol[i] = false;
viscol[j] = false;
}
return;
}
}
}
void workr(int pos, int type) {
if (solved) return;
if (pos == ) {
workc((m + ) / , m & );
return;
}
if (type) {
for (int i = ; i <= n; i++) {
visrow[i] = true;
rnum[pos] = i;
workr(pos - , );
visrow[i] = false;
}
} else {
for (int i = ; i <= n; i++) {
if (visrow[i]) continue;
for (int j = i + ; j <= n; j++)
if (!visrow[j] && row[i][j]) {
visrow[i] = true;
visrow[j] = true;
rnum[pos] = i;
rnum[n + - pos] = j;
workr(pos - , );
visrow[i] = false;
visrow[j] = false;
}
return;
}
}
}
int main() {
freopen("fragment.in", "r", stdin);
freopen("fragment.out", "w", stdout);
int T, num; read(num), read(T);
while (T--) {
read(n), read(m);
for (int i = ; i <= n; i++)
scanf("%s", mp[i] + );
for (int i = ; i <= n; i++)
for (int j = ; j <= n; j++) {
static char x[MAXN], y[MAXN];
for (int k = ; k <= m; k++) {
x[k] = mp[i][k];
y[k] = mp[j][k];
}
sort(x + , x + m + );
sort(y + , y + m + );
row[i][j] = true;
for (int k = ; k <= m; k++)
if (x[k] != y[k]) row[i][j] = false;
}
for (int i = ; i <= m; i++)
for (int j = ; j <= m; j++) {
static char x[MAXN], y[MAXN];
for (int k = ; k <= n; k++) {
x[k] = mp[k][i];
y[k] = mp[k][j];
}
sort(x + , x + n + );
sort(y + , y + n + );
col[i][j] = true;
for (int k = ; k <= n; k++)
if (x[k] != y[k]) col[i][j] = false;
}
solved = false;
workr((n + ) / , n & );
if (!solved) printf("NO\n");
}
return ;
}

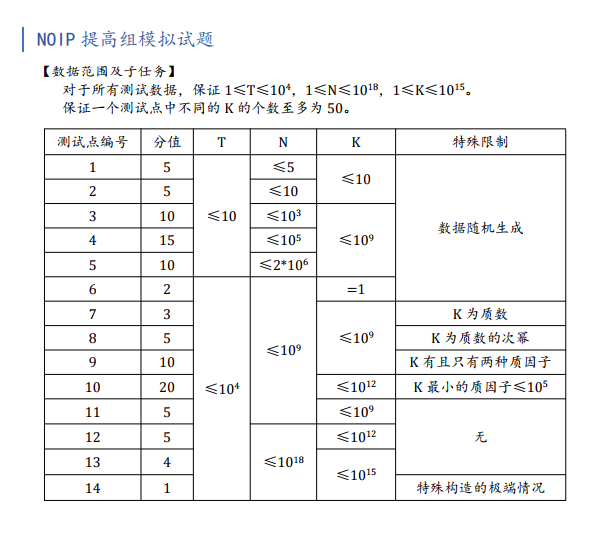
由于在K天之后必须所有的旅者都要回到他的家乡所以这n个人的初始序列按照题意模拟必须要是多个环,
且这些环的长度必须是k的质因数,那么这个问题就转变为对K进行质因数分解求出的所有质因数的多重集求和恰为n是否合法
我们现在考虑这个问题,
显然输入的K可能会有重复所以我们并不用每次对K都分解质因数,所以我们用memk[i]记录当前都多少不同种类的K ,q为当前数目
设当前是在memk数组中的第pos个K是当前的K那么p[pos][ ]为mem[pos]的质因数,个数记为cnt[pos]
讲了一大坨就是这个程序:
read(n), read(k);//读入n k
int pos = ; //找之前算过的k
for (int i = ; i <= q; i++)
if (memk[i] == k) pos = i; //找K
if (pos == ) {//没找到qwq
pos = ++q;
memk[q] = k;
long long tmp = k; //分解质因数tmp=k
for (int i = ; 1ll * prime[i] * prime[i] <= tmp; i++)
if (tmp % prime[i] == ) {
p[pos][++cnt[pos]] = prime[i];
while (tmp % prime[i] == ) tmp /= prime[i];
}
if (tmp != ) p[pos][++cnt[pos]] = tmp;//分解质因数
我们来讨论几种简单的情况
cnt[pos]=1那么如果这个仅存的质因数被n整除那么久不行,否则行
bool flg = false;
for (int i = ; i <= cnt[pos]; i++)//依次检测
if (n % p[pos][i] == ) {//行,那么就是true
printf("YES\n");
flg = true;
break;
}
if (flg) continue;
if (cnt[pos] <= ) {//否则就是false
printf("NO\n");
continue;
}
cnt[pos]=2的情况就是ax+by=n求是否存在正数解(a,b)那么就是ex_gcd
这里是ex_gcd的板子(求ax+by=gcd(a,b)求(x,y)的值)
void exgcd(long long a, long long b, long long &x, long long &y) {
if (b == ) {
x = ;
y = ;
return;
}
long long q = a / b, r = a % b;
exgcd(b, r, y, x);
y -= q * x;
}
考虑这样一个问题 已知xp1+yp2=gcd(p1,p2)=1求xp1+yp2=n的解
令x‘p1+y'p2=n成立,xp1+yp2=1成立
那么就有n(xp1+yp2)=n 所以nxp1+nyp2=n;
所以x'=nx,y'=ny,最小化y'(但是保证大于0)才可能让x’尽可能大直到x>0;
根据定理可知y‘最小为ny%p1,
证明的话就是那 一直从y中拿p1到不能拿为止这个时候就是y-[y/p1]*p1就是就是y%p1,加个n就是ny%p1
所以这里的p1放在全局看就是第一个质因数,p2就是第二个质因数
程序的话就是这样:
if (cnt[pos] == ) {
long long x = , y = ;
exgcd(p[pos][], p[pos][], x, y);
y = (y % p[pos][] + p[pos][]) % p[pos][];//求出最小的y
long long tmp = y * (n % p[pos][]) % p[pos][] * p[pos][]; //求出最大的x
if (tmp <= n) printf("YES\n"); //若最大的n不大于n就是true
else printf("NO\n");//否则是false
continue;
}
cnt[pos]>3怎办?
我们设dist[pos][i]表示第pos个数用所有除第一个质因子外乱加求和(带自定义权求和)得到的sum值%i最小是多少
我们考虑这样一个问题
n=xp1+y(x是p1的系数y是乱加求和sum和)显然要想n分解成立那么y必须要不大于n%p1,解释的话就是如果多了那么不用加y直接进加x就行了
这样我们可以用一个形如堆优化dijkstra算法就行求出最小的sum%i的值
if (cnt[pos] >= ) {
for (int i = ; i < p[pos][]; i++)
dist[pos][i] = INF;
static priority_queue <info> Heap;
dist[pos][] = ; Heap.push((info) {, });
//info有两个值dist和home,dist表示乱加数值的和,home表示%i后的余数
static bool vis[MAXN];
memset(vis, false, sizeof(vis));
while (!Heap.empty()) {
while (!Heap.empty() && vis[Heap.top().home]) Heap.pop();
if (Heap.empty()) break;
info tmp = Heap.top(); Heap.pop();
for (int i = ; i <= cnt[pos]; i++) {
int dest = (tmp.home + p[pos][i]) % p[pos][]; //乱加
if (dist[pos][dest] > tmp.dist + p[pos][i]) {
dist[pos][dest] = tmp.dist + p[pos][i];
Heap.push((info) {dist[pos][dest], dest});
}
}
}
}
}
判断的话就是这样:
int tmp = n % p[pos][];//就是y
if (dist[pos][tmp] <= n) printf("YES\n");//有乱加的sum%y<=n就一定可以
else printf("NO\n");
那么std如下:
#include<bits/stdc++.h>
using namespace std;
const int MAXQ = ;
const int MAXLOG = ;
const int MAXN = ;
const int MAXP = 2e6 + ;
const int MAXV = 3.2e7 + ;
const long long INF = 4e18;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); }
template <typename T> void read(T &x) {
x = ; int f = ;
char c = getchar();
for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
for (; isdigit(c); c = getchar()) x = x * + c - '';
x *= f;
}
template <typename T> void write(T x) {
if (x < ) x = -x, putchar('-');
if (x > ) write(x / );
putchar(x % + '');
}
template <typename T> void writeln(T x) {
write(x);
puts("");
}
int q; long long memk[MAXQ];
int tot, prime[MAXP], f[MAXV];
int cnt[MAXQ]; long long p[MAXQ][MAXLOG];
long long dist[MAXQ][MAXN];
struct info {long long dist; int home; };
bool operator < (info a, info b) {
return a.dist > b.dist;
}
void exgcd(long long a, long long b, long long &x, long long &y) {
if (b == ) {
x = ;
y = ;
return;
}
long long q = a / b, r = a % b;
exgcd(b, r, y, x);
y -= q * x;
}
int main() {
freopen("fantasy.in", "r", stdin);
freopen("fantasy.out", "w", stdout);
int num; read(num);
for (int i = ; i < MAXV; i++) {
if (f[i] == ) prime[++tot] = f[i] = i;
for (int j = ; j <= tot && prime[j] <= f[i]; j++) {
int tmp = prime[j] * i;
if (tmp >= MAXV) break;
f[tmp] = prime[j];
}
}
int T; read(T);
while (T--) {
long long n, k;
read(n), read(k);
int pos = ;
for (int i = ; i <= q; i++)
if (memk[i] == k) pos = i;
if (pos == ) {
pos = ++q;
memk[q] = k;
long long tmp = k;
for (int i = ; 1ll * prime[i] * prime[i] <= tmp; i++)
if (tmp % prime[i] == ) {
p[pos][++cnt[pos]] = prime[i];
while (tmp % prime[i] == ) tmp /= prime[i];
}
if (tmp != ) p[pos][++cnt[pos]] = tmp;
if (cnt[pos] >= ) {
for (int i = ; i < p[pos][]; i++)
dist[pos][i] = INF;
static priority_queue <info> Heap;
dist[pos][] = ; Heap.push((info) {, });
static bool vis[MAXN];
memset(vis, false, sizeof(vis));
while (!Heap.empty()) {
while (!Heap.empty() && vis[Heap.top().home]) Heap.pop();
if (Heap.empty()) break;
info tmp = Heap.top(); Heap.pop();
for (int i = ; i <= cnt[pos]; i++) {
int dest = (tmp.home + p[pos][i]) % p[pos][];
if (dist[pos][dest] > tmp.dist + p[pos][i]) {
dist[pos][dest] = tmp.dist + p[pos][i];
Heap.push((info) {dist[pos][dest], dest});
}
}
}
}
}
bool flg = false;
for (int i = ; i <= cnt[pos]; i++)
if (n % p[pos][i] == ) {
printf("YES\n");
flg = true;
break;
}
if (flg) continue;
if (cnt[pos] <= ) {
printf("NO\n");
continue;
}
if (cnt[pos] == ) {
long long x = , y = ;
exgcd(p[pos][], p[pos][], x, y);
y = (y % p[pos][] + p[pos][]) % p[pos][];
long long tmp = y * (n % p[pos][]) % p[pos][] * p[pos][];
if (tmp <= n) printf("YES\n");
else printf("NO\n");
continue;
}
int tmp = n % p[pos][];
if (dist[pos][tmp] <= n) printf("YES\n");
else printf("NO\n");
}
return ;
}
HGOI20180813 (NOIP2018 提高组 Day2 模拟试题)的更多相关文章
- HGOI20180812 (NOIP2018 提高组 Day1 模拟试题)
前缀数组其实就是有序的,那么答案显然是 我们尝试求出通项公式: 证明如下: 因为 所以: 解之得: 更加通俗的写法如下: 易知 令 那么, (错位相减) 由易知等式代入得, 所以, 所以程 ...
- NOIP2018提高组Day2 解题报告
前言 关于\(NOIP2018\),详见此博客:NOIP2018学军中学游记(11.09~11.11). \(Day2\)的题目和\(Day1\)比起来,真的是难了很多啊. \(T1\):旅行(点此看 ...
- 冲刺NOIP2015提高组复赛模拟试题(五)2.道路修建
2.道路修建 描述 Description liouzhou_101最悲痛的回忆就是NOI2011的道路修建,当时开了系统堆栈,结果无限RE… 出于某种报复心理,就把那题神奇了一下: 在 Z星球上有N ...
- CCF-NOIP-2018 提高组(复赛) 模拟试题(四)
T1 贪吃蛇 [问题描述] 贪吃蛇是一个好玩的游戏.在本题中,你需要对这个游戏进行模拟. 这个游戏在一个 \(n\) 行 \(m\) 列的二维棋盘上进行. 我们用 \((x, y)\) 来表示第 \( ...
- CCF-NOIP-2018 提高组(复赛) 模拟试题(九)(2018 CSYZ长沙一中)
T1 Circle [问题描述] 小 w 的男朋友送给小 w 一个 n 个点 m 条边的图,并且刁难小 w 要她找出点数最少的正环. 小 w 不会做,于是向你求助. [输入格式] 第一行两个整数\(n ...
- CCF-NOIP-2018 提高组(复赛) 模拟试题(七)
T1 Adjoin [问题描述] 定义一种合法的\(0-1\)串:串中任何一个数字都与\(1\)相邻.例如长度为$ 3 的 0-1 $串中,\(101\)是非法的,因为两边的\(1\)没有相邻的\(1 ...
- CCF-NOIP-2018 提高组(复赛) 模拟试题(一)
T1 帽子戏法 问题描述 小 Y 有一个\(n*n*n\)的"帽子立方体" ,即一个\(n\)层的立方体,每层的帽子都 可以排成\(n*n\)的矩阵. "帽子立方体&qu ...
- 破译情报-NOIP2016提高组复赛模拟试题
[题目描述] 最近国安人员截获了一份 RB 国的秘密情报, 全文都是经过加密的,每个单 词都很长.破译人员想到先把单词化简一下,方法是把每个单词尽量取短些的前 缀,但所取的前缀不能是其他单词的前缀. ...
- 冲刺NOIP2015提高组复赛模拟试题(五) 3.破坏基地
3.破坏基地 描述 Description 在Z国和W国之间一直战火不断. 好不容易,W国的间谍把完整的Z国的军事基地的地图到手了. 于是W国决定再次出击,一举击破Z国的防线. W国认真研究了Z国的地 ...
随机推荐
- 20155307实验八 《网络对抗》 Web基础
20155307实验八 <网络对抗> Web基础 实验过程 Web前端:HTML 使用netstat -aptn查看80端口是否被占用(上次实验设置为Apache使用80端口),如果被占用 ...
- 20155320 Exp6 信息搜集与漏洞扫描
20155320 Exp6 信息搜集与漏洞扫描 [实验后回答问题] (1)哪些组织负责DNS,IP的管理. 全球根服务器均由美国政府授权的ICANN统一管理,负责全球的域名根服务器.DNS和IP地址管 ...
- JavaEE笔记(十二)
代理的三种配置 beans配置文件 <?xml version="1.0" encoding="UTF-8"?> <beans xmlns=& ...
- 【Qt】QOpenGLWidget展示蒙版效果
关键代码是派生QOpenGLWidget,覆写paintEvent函数 QPainter p; p.begin(this); p.drawImage(QPoint(, ), m_Img); QLine ...
- 您需要来自XXX的权限才能对此文件夹进行更改
解决办法: cmd命令:del/f/s/q 文件夹
- C语言与数据库操作入门(Win版)
C语言与数据库操作入门(Win版) 2017年12月10日 17:30:17 阅读数:1387 数据库,DataBase,学C语言的是不是想说,很想爱她却并不容易呢?不用着急,C语言也可以操作数据库的 ...
- JS基础内容小结(event 鼠标键盘事件)(三)
var ev=ev||event 兼容性处理 得到焦点为 onfocus 失去焦点 onblur return false能阻止部分函数的执行 obj.select 选择指定元素里的文本内容 ———— ...
- CSS技巧收集——毛玻璃效果
先上 demo和 源码 其实毛玻璃的模糊效果技术上比较简单,只是用到了 css 滤镜(filter)中的 blur 属性.但是要做一个好的毛玻璃效果,需要注意很多细节. 比如我们需要将上图中页面中间的 ...
- OpenGL学习(2)——绘制三角形(补)
对上一篇的补充,通过绘制三角形来完成矩形的绘制.此外,完成章节后练习. 绘制矩形 一个矩形由两个三角形组成,因此绘制矩形需要绘制两个三角形,一共6个顶点,其中2个顶点重复画了两次. 为了减小开销,仅储 ...
- 剑指offer——滑动窗口的最大值
给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值.例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6, ...
