洛谷 P2224 [HNOI2001]产品加工 解题报告

P2224 [HNOI2001]产品加工

题目描述

某加工厂有A、B两台机器，来加工的产品可以由其中任何一台机器完成，或者两台机器共同完成。由于受到机器性能和产品特性的限制，不同的机器加工同一产品所需的时间会不同，若同时由两台机器共同进行加工，所完成任务又会不同。某一天，加工厂接到n个产品加工的任务，每个任务的工作量不尽一样。

你的任务就是：已知每个任务在A机器上加工所需的时间t1, B机器上加工所需的时间t2及由两台机器共同加工所需的时间t3，请你合理安排任务的调度顺序，使完成所有n个任务的总时间最少。

输入输出格式

输入格式：

（输入文件共n+1行）

第1行为 n。 n是任务总数（1≤n≤6000）

第i+1行为3个[0，5]之间的非负整数t1,t2,t3，分别表示第i个任务在A机器上加工、B机器上加工、两台机器共同加工所需要的时间。如果所给的时间t1或t2为0表示任务不能在该台机器上加工，如果t3为0表示任务不能同时由两台机器加工。

输出格式：

最少完成时间

---

这个DP没见过的话估计很难想出来。

时间肯定要压进去一维，但这两个机器是并行的，看起来非常难存储与转移状态。

思考方向我没什么想法，只好直接介绍方法了。

令\(dp[i][j]\)代表前\(i\)件物品全部处理时\(A\)机器用时\(j\)时\(B\)机器的最小用时。

注意两台机器的状态被拆成了里面和外面。

转移

\(dp[i][j]=min(dp[i-1][j]-c_{iA},dp[i-1][j]+c_{iB},dp[i-1][j-c_{iC}]+c_{iC})\)

空间会爆，所以采用滚动数组优化。

这题还卡常，所以如果特判不存在或者每次清0滚动数组会T，解决方法是读入是直接把0赋值成inf，注意inf不要太大，否则可能会爆int

但还是会T，我们加上时间的上界优化

---

2018.6.28 晚 21.50更新

同机房的神犇发现了一个问题，在这里提一下。

在转移同时操作（操作3）时为什么这样是合法的

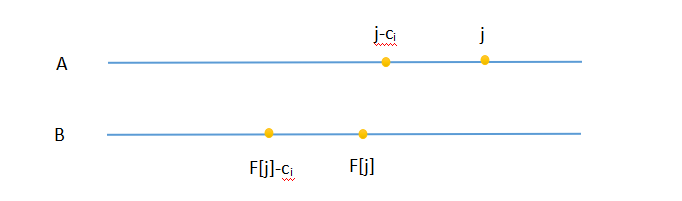
确实，看起来并不是并行的。

这么理解，我们其实并不关心这个方案是怎么放的。

所以我们把所有的并行操作放在一起最前面就行啦

把\(dp[i][j]\)数组的意义改一下。

\(dp[i][j]\)表示在\(j\)时刻一共运行了\(max(j,dp[i][j])\)时间时处理完所有物品的最小值

他的解释方法产品加工

---

Code:

#include <cstdio>
#include <cstring>
int max(int x,int y){return x>y?x:y;}
int min(int x,int y){return x<y?x:y;}
const int inf=30010;
int n,c[3],dp[inf],ans=inf,r;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n*5;i++)
        dp[i]=inf;
    dp[0]=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d",c,c+1,c+2);
        r+=max(c[0],max(c[1],c[2]));
        if(!c[0]) c[0]=inf;
        if(!c[1]) c[1]=inf;
        if(!c[2]) c[2]=inf;
        for(int j=r;j>=0;j--)
        {
            dp[j]+=c[1];
            if(j>=c[0])
                dp[j]=min(dp[j],dp[j-c[0]]);
            if(j>=c[2])
                dp[j]=min(dp[j],dp[j-c[2]]+c[2]);
        }
    }
    for(int i=0;i<=r;i++)
        ans=min(ans,max(dp[i],i));
    printf("%d\n",ans);
    return 0;
}

---

2018.6.28