HDU-6514 Monitor（二维前缀和+差分）

http://acm.hdu.edu.cn/showproblem.php?pid=6514

Problem Description

Xiaoteng has a large area of land for growing crops, and the land can be seen as a rectangle of n×m. 
But recently Xiaoteng found that his crops were often stolen by a group of people, so he decided to install some monitors to find all the people and then negotiate with them.
However, Xiao Teng bought bad monitors, each monitor can only monitor the crops inside a rectangle. There are p monitors installed by Xiaoteng, and the rectangle monitored by each monitor is known. 
Xiao Teng guess that the thieves would also steal q times of crops. he also guessed the range they were going to steal, which was also a rectangle. Xiao Teng wants to know if his monitors can see all the thieves at a time.

Input

There are mutiple test cases.
Each case starts with a line containing two integers n,m(1≤n,1≤m,n×m≤107) which represent the area of the land.
And the secend line contain a integer p(1≤p≤106) which represent the number of the monitor Xiaoteng has installed. This is followed by p lines each describing a rectangle. Each of these lines contains four intergers x1,y1,x2 and y2(1≤x1≤x2≤n,1≤y1≤y2≤m) ,meaning the lower left corner and upper right corner of the rectangle.
Next line contain a integer q(1≤q≤106) which represent the number of times that thieves will steal the crops.This is followed by q lines each describing a rectangle. Each of these lines contains four intergers x1,y1,x2 and y2(1≤x1≤x2≤n,1≤y1≤y2≤m),meaning the lower left corner and upper right corner of the rectangle.

Output

For each case you should print q lines.
Each line containing YES or NO mean the all thieves whether can be seen.

Sample Input

Sample Output

YES
NO

Hint

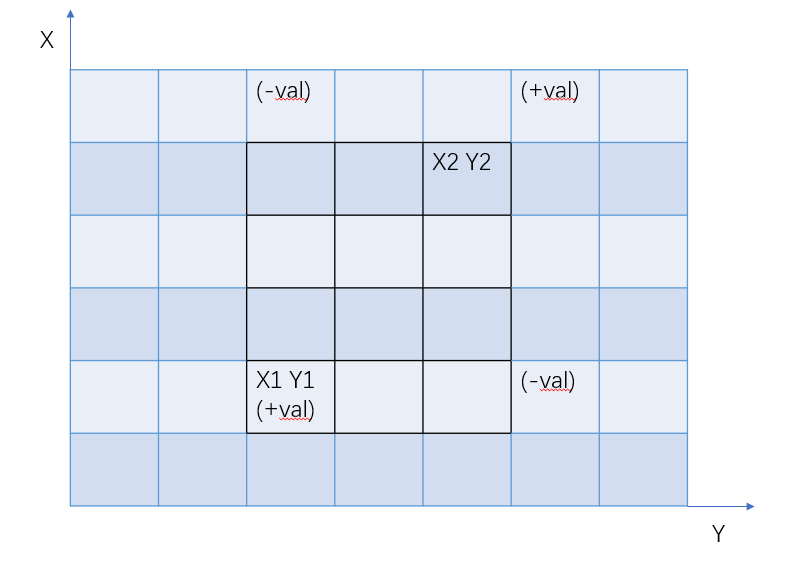
In the picture,the red solid rectangles mean the monitor Xiaoteng installed, and the blue dotted rectangles mean the area will be stolen.

(x1,y1)为矩形左下角,(x2,y2)为矩形右下角，竖直向上为x正方向，水平向右为y正方向

题意：

在一个面积不超过n*m的矩形上，有p个矩形A，问之后的q个矩形B能否被之前的A全部覆盖。

思路：

由于n*m,p,q的范围过大，于是考虑O(n*m+p+q)的做法，即二维前缀和+差分。

对于A类矩形(x1,y1,x2,y2)，我们只需要在(x1,y1),(x2+1,y2+1)处+1，在(x1,y2+1),(x2+1,y1)处-1 ，

之后对整个面积求一个前缀和，则大于0的地方就是被A类矩形覆盖的点。

把值大于0的地方变成1，再一次求一次前缀和，处理好后即可在O(1)的时间算出一个矩形内被覆盖的点的数量。
（详细见注释）

亮点：

二维数组化为一维

两次求前缀和，重新赋值

代码如下：

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <string>
 #include <math.h>
 #include <algorithm>
 #include <vector>
 #include <stack>
 #include <queue>
 #include <set>
 #include <map>
 #include <math.h>
 const int INF=0x3f3f3f3f;
 typedef long long LL;
 const int mod=1e9+;
 //const double PI=acos(-1);
 const int maxn=1e7+;
 using namespace std;

 int a[maxn];//二维化为一维
 int n,m;

 void Add(int x,int y,int val)//添加标记
 {
     if(x>n||y>m)
         return;
     a[(x-)*m+y]+=val;
 }

 int Query(int x,int y)//得到该处的值，主要用来处理边界0
 {
     if(x==||y==)
         return ;
     return a[(x-)*m+y];
 }

 void Sum()//求前缀和
 {
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=m;j++)
         {
             a[(i-)*m+j]+=Query(i,j-)+Query(i-,j)-Query(i-,j-);
         }
     }
 }

 int main()
 {
     while(~scanf("%d %d",&n,&m))
     {
         memset(a,,sizeof(a));
         int x1,x2,y1,y2;
         int p,q;
         scanf("%d",&p);
         while(p--)
         {
             scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
             Add(x1,y1,);
             Add(x2+,y2+,);
             Add(x1,y2+,-);
             Add(x2+,y1,-);
         }
         Sum();//第一次求二维前缀和，a[i]>0说明该处被覆盖过
         for(int i=;i<=n;i++)//将被覆盖的点重新赋值为1，便于判断
         {
             for(int j=;j<=m;j++)
             {
                 if(a[(i-)*m+j])
                     a[(i-)*m+j]=;
             }
         }
         Sum();//第二次求前缀和，得到的结果即为矩形内被染色的面积
         scanf("%d",&q);
         while(q--)
         {
             scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
             int ans=Query(x2,y2)-Query(x1-,y2)-Query(x2,y1-)+Query(x1-,y1-);//利用前缀和得出矩形内被染色的面积
             if(ans==(x2-x1+)*(y2-y1+))//看染色的面积是否等于矩形的总面积
                 printf("YES\n");
             else
                 printf("NO\n");
         }
     }
     return ;
 }