[Python]机器学习：PageRank原理与实现

前言

PageRank是TextRank的前身。顾名思义，TextRank用于文本重要性计算(语句排名)和文本摘要等NLP应用，而Page最初是因搜索引擎需要对网页的重要性计算和排名而诞生。本着追本溯源、知其然要知其所以然的目的，而进行实践层面的研究和实现。

网上博客很多，但真正把一件事情讲懂，讲清楚的，一直很少。我来试试，把原理和编程实现一并说个明白。

+  作者：Johnny Zen
+  单位：西华大学 计算机学院
+  博文地址：https://www.cnblogs.com/johnnyzen/p/10888248.html
+  CSDN警告：版权所有，侵权必究。

附一张手记以作纪念，哈哈~

一 PageRank原理

鸣谢

原理的部分概述、三个例子和公式推导，来源于博文：PageRank算法原理与实现

大部分配图与公式为本文博主通过markdown编辑。

1.1 PageRank概述

PageRank，又称网页排名、谷歌左侧排名，是一种由搜索引擎根据网页之间相互的超链接计算的技术，而作为网页排名的要素之一，以Google公司创办人拉里·佩奇（Larry Page）之姓来命名。Google用它来体现网页的相关性和重要性，在搜索引擎优化操作中是经常被用来评估网页优化的成效因素之一。

TextRank论文中对PageRank的一点建议：将最初PageRank基于无权边的图模型改进为有权图。通过有权边来表示两节点间的“强度”，进而可能提高模型效果。

In the context of Web surfing, it is unusual for a page to include multiple or partial links to another page, and hence the original PageRank definition for graph-based ranking is assuming unweighted graphs.However, in our model the graphs are build from natural language texts, and may include multiple or partial links between the units (vertices) that are extracted from text. It may be therefore useful to indicate and incorporate into the model the “strength” of the connection between two vertices Vi and Vj as a weight W(i,j) added to the corresponding edge that connects the two vertices.

1.2 PageRank原理

举个栗子

• ①假设一个由4个网页组成的群体：A，B，C和D。如果所有页面都只链接至A，那么A的PR（PageRank）值将是B，C及D的Pagerank总和。

那么，有：
$$ PR(A)=PR(B)+PR(C)+PR(D) $$

• ②假设一个由4个网页组成的群体：A，B，C和D。重新假设B链接到A和C，C只链接到A，并且D链接到全部其他的3个页面。

那么，有：
$$ PR(A)=PR(B)/2 + PR(C)/1 + PR(D)/3 $$

公式推导

+ S(Vi)：网页i的中重要性（PR值）
+ d：阻尼系数。其意义是，在任意时刻，用户到达某页面后并继续向后浏览的概率；该数值是根据上网者使用浏览器书签的平均频率估算而得，通常d=0.85
+ In(Vi)：存在指向网页i的链接的网页集合
+ Out(Vj)：网页j中的链接存在的链接指向的网页的集合。|Out(Vj)|是集合中元素的个数

换成我们容易理解的公式。 即

\[PA(A) = (1-d) + d*\begin{bmatrix} \frac{ PR(T_{_{1}}) }{ |Out(T_{_{1}})| } +\frac{ PR(T_{_{2}}) }{ |Out(T_{_{2}})| } + ... + \frac{ PR(T_{_{m}}) }{ |Out(T_{_{m}})| } \end{bmatrix}\quad
\]

\[TR(Ti) = (1-d) + d*\begin{bmatrix} \frac{ TR(T_{_{1}})*Similarity(Ti,T1) }{ |Out(T_{_{1}})| } +\frac{ PR(T_{_{2}})*Similarity(Ti,T2) }{ |Out(T_{_{2}})| } + ... + \frac{ PR(T_{_{m}})*Similarity(Ti,Tm) }{ |Out(T_{_{m}})| } \end{bmatrix}\quad
\]

• PR(A)：页面节点A的PR值。其中m，即 所有指向页面节点A的节点个数
• PA(Ti)：指向A的所有页面中的其中某一页面Ti的PR值
• d：阻尼系数
• |Out(Ti)|：Ti指向其它页面的个数 即 出度个数
• |In(Ti)|：指向Ti页面节点的个数 即 入度个数

公式版本2

\[ PA(A) = \frac{(1-d)}{d} + d*\begin{bmatrix}
\frac{ PR(T_{_{1}}) }{ |Out(T_{_{1}})| } +\frac{ PR(T_{_{2}}) }{ |Out(T_{_{2}})| } + ... + \frac{ PR(T_{_{m}}) }{ |Out(T_{_{m}})| } \end{bmatrix}\quad \]

其中，N为页面节点总数。

二 PageRank编程实践

• 举个例子。假设每个页面节点的初始PR值为1，阻尼系数d=0.5；页面关系如下：

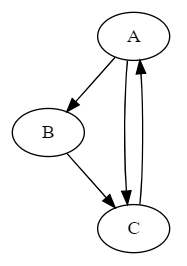
• PR(A)

\[PR(A) = 0.5 + 0.5*PR(C)=0.5+0.5*(1) = 1
\]

• PR(B)

\[PR(B) = 0.5 + 0.5*PR(A)/2 =0.5+0.5*(1/2)= 0.75
\]

• PR(C)

\[PR(C) = 0.5 + 0.5*(PR(A)/2 + PR(B)/1) = 0.5+0.5*(1/2+0.75)= 1.125
\]

• 不断迭(xun)代(huan)计算

什么时候迭代可以停止？PR收敛的时候。具体实施时，可以：①设置迭代过程中，两次PR计算的差值的停止阈值 ②设置最大迭代计算次数等

2.1 PageRank类设计

环境

python 3.6.2

• PageRank：class
  • init(self,pages=['A','B'],links=[(1,0),(0,1)],d=0.85)
  • getInputLinksList(self) # 获得每一页面节点对应的入度节点
    • 形如：[[2], [0], [0, 1]]
  • getOutputLinksList(self) # 获得每一页面节点对应的出度节点
    • 形如：[[1, 2], [2], [0]]
  • getCurrentPageRanks() # 获得当前pr值
    • 形如：[ 1.07692308 0.76923077 1.15384615]
  • iterOnce # [static] 对所有页面节点，迭代一次。需要传入当前pr值，返回 迭代后的pr值。
    • 形如：[ 1.07692308 0.76923077 1.15384615]
  • maxAbs(array) # [static] 获得数组array中绝对值最大的元素下标
  • train(self,maxIterationSize=100,threshold=0.0000001)

import numpy as np;

class PageRank:
    def __init__(self,pages=['A','B'],links=[(1,0),(0,1)],d=0.85):
        self.pages = pages;
        self.links = links;
        # 根据初始数据初始化其它参数
        self.dtype = np.float64; #精度更高
        self.d = d; # 阻尼系数
        self.pageRanks = np.array([ 1/(len(self.pages)) ]*len(self.pages)); # np.ones(len(self.pages), dtype = self.dtype); # 初始化每个页面PR值：1 or 1 / N or other 【利用numpy数组化，方便进行算术运算，原生python列表不支持此类运算】经过几组数据测试，此初始值确实不会影响最终的PR收敛值
        ## 记录每个节点的入度节点列表 (不定长二维数组)
        self.inputLinksList = [[]]*len(self.pages); #  创建不定长二维数组 [[], [], [], [],...,[]]
        for i in range(len(self.inputLinksList)):
            self.inputLinksList[i]=[];
            pass;
        # print("in:\n",self.inputLinksList)
        for item in self.links: # (n,m)：n指向m
        #     print(i)
            self.inputLinksList[item[1]].append(item[0]);
            pass;
        ## 记录每个节点的出度节点列表 (不定长二维数组)
        self.outputLinksList = [[]]*len(pages); #  创建不定长二维数组 [[], [], [], [],...,[]]
        for item in range(len(self.outputLinksList)):
            self.outputLinksList[item]=[];
            pass;
        # print("out:\n",self.outputLinksList)
        for item in self.links: # (n,m)：n指向m
        #     print(i)
            self.outputLinksList[item[0]].append(item[1]);
            pass;

    def getInputLinksList(self):
        # print("in:\n",self.inputLinksList)
        return self.inputLinksList;

    def getOutputLinksList(self):
        # print("out:\n",self.getOutputLinksList)
        return self.outputLinksList;

    def getCurrentPageRanks():
        return self.pageRanks;

    def getLinks():
        return self.links;

    def iterOnce(pageRanks,d,links,inputLinksList,outputLinksList): #迭代运算一次 [本函数可以抽离出栏单独使用，类似于静态方法]
        pageRanks = np.copy(pageRanks); #必须拷贝，否则后续影响传入地址pageRanks的值
        # print("input pageRanks:",pageRanks);
        # print("input d:",d);
        for i in range(0,len(pageRanks)):
            result = 0.0;
            for j in inputLinksList[i]: # inputLinksList[i]：第i个节点的(入度)节点[下标]列表
                # print (inputLinksList[i]);
                result += pageRanks[j]/len(outputLinksList[j]);
                # print("[",j,"] pageRanks[j]:",pageRanks[j]," len(outputLinksList[j]:",len(outputLinksList[j]));
                pass;
            # print("[",i,"] result:",result);
            pageRanks[i] = (1 - d) + d*result;
            # print("[",i,"] pr:",pageRanks[i]);
            pass;
        return pageRanks;

    def maxAbs(array): # 从数组中找绝对值最大者 [静态方法]
        max = 0; # 初始化 默认第一个为绝对值最小值的下标
        for i in range(0,len(array)):
            if abs(array[max]) < abs(array[i]):
                max = i;
                pass;
            pass;
        return max; # 返回下标

    def train(self,maxIterationSize=100,threshold=0.0000001): # 训练 threshold：阈值
        print("[PageRank.train]",0," self.pageRanks:",self.pageRanks);
        iteration=1;
        lastPageRanks = self.pageRanks; # pageRanks:上一批次  self.pageRanks：当前批次
        difPageRanks = np.array([100000.0]*len(self.pageRanks),dtype=self.dtype); # 初始化 当前批次各节点PR值与上一批次PR值的大小 [1000000000,1000000000, ...,1000000000]
        while iteration <= maxIterationSize:
            if ( abs(difPageRanks[PageRank.maxAbs(difPageRanks)]) < threshold ):
                break;
            self.pageRanks = PageRank.iterOnce(lastPageRanks,self.d,self.links,self.inputLinksList,self.outputLinksList);
            #【利用numpy数组化，方便进行加减算术运算，原生python列表不支持此类运算】
            difPageRanks = lastPageRanks - self.pageRanks ; # self.pageRanks在初始化__init__中已通过numpy向量化
            # print("[PageRank.train]",iteration," lastPageRanks:",lastPageRanks);
            print("[PageRank.train]",iteration," self.pageRanks:",self.pageRanks);
            # print("[PageRank.train]",iteration," difPageRanks:",difPageRanks);
            lastPageRanks = np.array(self.pageRanks);
            iteration += 1;
            pass;
        print("[PageRank.train] iteration:",iteration-1);#test
        print("[PageRank.train] difPageRanks:",difPageRanks) # test
        return self.pageRanks;

    pass; # end class

2.2 调用示例

``` python
# 用户初始化页面链接数据
#pages = ["A","B","C","D"];
#links = [(1,0),(1,2),(2,0),(3,0),(3,1),(3,2)]; # (n,m)：n指向m
pages = ["A","B","C"];
links = [(0,1),(0,2),(1,2),(2,0)]; # (n,m)：n指向m
d = 0.5; # 阻尼系数

pageRank = PageRank(pages,links,d);

pageRanks = pageRank.train(12,0.000000000001); # pageRanks:各节点的PR值

print("pageRanks:",pageRanks);

print("sum(pageRanks) :",np.sum(pageRanks));

print("getInputLinksList:",pageRank.getInputLinksList());

print("getOutputLinksList:",pageRank.getOutputLinksList());

``` python
// output ：PR初始值为1时
[PageRank.train] 0  self.pageRanks: [ 1.  1.  1.]
[PageRank.train] 1  self.pageRanks: [ 1.     0.75   1.125]
[PageRank.train] 2  self.pageRanks: [ 1.0625     0.765625   1.1484375]
[PageRank.train] 3  self.pageRanks: [ 1.07421875  0.76855469  1.15283203]
[PageRank.train] 4  self.pageRanks: [ 1.07641602  0.769104    1.15365601]
[PageRank.train] 5  self.pageRanks: [ 1.076828   0.769207   1.1538105]
[PageRank.train] 6  self.pageRanks: [ 1.07690525  0.76922631  1.15383947]
[PageRank.train] 7  self.pageRanks: [ 1.07691973  0.76922993  1.1538449 ]
[PageRank.train] 8  self.pageRanks: [ 1.07692245  0.76923061  1.15384592]
[PageRank.train] 9  self.pageRanks: [ 1.07692296  0.76923074  1.15384611]
[PageRank.train] 10  self.pageRanks: [ 1.07692305  0.76923076  1.15384615]
[PageRank.train] 11  self.pageRanks: [ 1.07692307  0.76923077  1.15384615]
[PageRank.train] 12  self.pageRanks: [ 1.07692308  0.76923077  1.15384615]
[PageRank.train] iteration: 12
[PageRank.train] difPageRanks: [ -3.35654704e-09  -8.39136760e-10  -1.25870514e-09]
pageRanks: [ 1.07692308  0.76923077  1.15384615]
sum(pageRanks) : 2.99999999874
getInputLinksList: [[2], [0], [0, 1]]
getOutputLinksList: [[1, 2], [2], [0]]

//output ：PR初始值为1/N时
[PageRank.train] 0  self.pageRanks: [ 0.33333333  0.33333333  0.33333333]
[PageRank.train] 1  self.pageRanks: [ 0.66666667  0.66666667  1.        ]
[PageRank.train] 2  self.pageRanks: [ 1.     0.75   1.125]
[PageRank.train] 3  self.pageRanks: [ 1.0625     0.765625   1.1484375]
[PageRank.train] 4  self.pageRanks: [ 1.07421875  0.76855469  1.15283203]
[PageRank.train] 5  self.pageRanks: [ 1.07641602  0.769104    1.15365601]
[PageRank.train] 6  self.pageRanks: [ 1.076828   0.769207   1.1538105]
[PageRank.train] 7  self.pageRanks: [ 1.07690525  0.76922631  1.15383947]
[PageRank.train] 8  self.pageRanks: [ 1.07691973  0.76922993  1.1538449 ]
[PageRank.train] 9  self.pageRanks: [ 1.07692245  0.76923061  1.15384592]
[PageRank.train] 10  self.pageRanks: [ 1.07692296  0.76923074  1.15384611]
[PageRank.train] 11  self.pageRanks: [ 1.07692305  0.76923076  1.15384615]
[PageRank.train] 12  self.pageRanks: [ 1.07692307  0.76923077  1.15384615]
[PageRank.train] iteration: 12
[PageRank.train] difPageRanks: [ -1.79015842e-08  -4.47539605e-09  -6.71309408e-09]
pageRanks: [ 1.07692307  0.76923077  1.15384615]
sum(pageRanks) : 2.99999999329
getInputLinksList: [[2], [0], [0, 1]]
getOutputLinksList: [[1, 2], [2], [0]]

留个小问题，如何证明/保证PageRank经过n次迭代以后，必然收敛？即 收敛一定会成立吗？试证明之。

三 文献

• 参考文献
  • PageRank算法原理与实现
• 推荐文献
  • Textrank算法介绍
  • 简易中文自动文摘系统（四）：TextRank算法实现
  • TextRank: Bringing Order into Text.
  • Python：创建二维不定长数组