洛谷P2569 (BZOJ1855)[SCOI2010]股票交易【单调队列优化DP】

Description

最近lxhgww又迷上了投资股票，通过一段时间的观察和学习，他总结出了股票行情的一些规律。通过一段时间的观察，lxhgww预测到了未来T天内某只股票的走势，第i天的股票买入价为每股APi，第i天的股票卖出价为每股BPi（数据保证对于每个i，都有APi>=BPi），但是每天不能无限制地交易，于是股票交易所规定第i天的一次买入至多只能购买ASi股，一次卖出至多只能卖出BSi股。另外，股票交易所还制定了两个规定。为了避免大家疯狂交易，股票交易所规定在两次交易（某一天的买入或者卖出均算是一次交易）之间，至少要间隔W天，也就是说如果在第i天发生了交易，那么从第i+1天到第i+W天，均不能发生交易。同时，为了避免垄断，股票交易所还规定在任何时间，一个人的手里的股票数不能超过MaxP。在第1天之前，lxhgww手里有一大笔钱（可以认为钱的数目无限），但是没有任何股票，当然，T天以后，lxhgww想要赚到最多的钱，聪明的程序员们，你们能帮助他吗？

Input

输入数据第一行包括3个整数，分别是T，MaxP，W。接下来T行，第i行代表第i-1天的股票走势，每行4个整数，分别表示APi，BPi，ASi，BSi。

Output

输出数据为一行，包括1个数字，表示lxhgww能赚到的最多的钱数。

Sample Input

5 2 0
2 1 1 1
2 1 1 1
3 2 1 1
4 3 1 1
5 4 1 1

Sample Output

HINT

对于30%的数据，0 < =W 对于50%的数据，0 < =W 对于100%的数据，0 < =W
对于所有的数据，1 < =BPi < =APi < =1000,1 < =ASi,BSi < =MaxP

题解：设f[i][j]表示第i天持有j股股票能获得的做大利润

对于买入，我们可以变形：

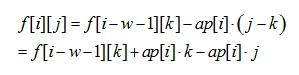
那么可以用单调队列维护f[i-w-1][k]+ap[i]*k（因为对于固定的i，ap[i]是固定的），这样f[i][j]就能做到O(1)计算，而不必枚举k。卖出也一样。

参考代码：

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

#define pii pair<int,int>

#define pil pair<int,ll>

#define mkp make_pair

#define fi first

#define se second

const int INF=0x3f3f3f3f;

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-') f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=(x<<)+(x<<)+ch-'';ch=getchar();}

    return x*f;

}

const int maxn=;

int n,m,w;

int dp[maxn][maxn],q[maxn];

int main()

{

    n=read();m=read();w=read();

    int ap,bp,as,bs,ans=;

    memset(dp,,sizeof(dp));

    for(int i=;i<=n;++i)

    {

        ap=read();bp=read();as=read();bs=read();

        for(int j=;j<=as;++j) dp[i][j]=-j*ap;//直接购买股票

        for(int j=;j<=m;++j) dp[i][j]=max(dp[i][j],dp[i-][j]);//未到第w+1天不能出售

        if(i<=w) continue;

        int l=,r=;

        for(int j=;j<=m;++j)//在之前的基础上买股票

        {

            while(l<r && q[l]<j-as) ++l;//把超出范围的去掉

            while(l<r&&dp[i-w-][q[r-]]+q[r-]*ap<=dp[i-w-][j]+j*ap) --r;

            q[r++]=j;

            if(l<r) dp[i][j]=max(dp[i][j],dp[i-w-][q[l]]+q[l]*ap-j*ap);

        }

        l=,r=;

        for(int j=m;j>=;--j)//在之前的基础上卖股票

        {

            while(l<r && q[l]>j+bs) ++l;

            while(l<r&&dp[i-w-][q[r-]]+q[r-]*bp<=dp[i-w-][j]+j*bp) --r;

            q[r++]=j;

            if(l<r) dp[i][j]=max(dp[i][j],dp[i-w-][q[l]]+q[l]*bp-j*bp);

        }

    }

    for(int i=;i<=m;++i) ans=max(ans,dp[n][i]);

    printf("%d\n",ans);

    return ;

}