CF 526F Max Mex(倍增求LCA+线段树路径合并)

Max Mex

题目地址：https://codeforces.com/contest/1084/problem/F

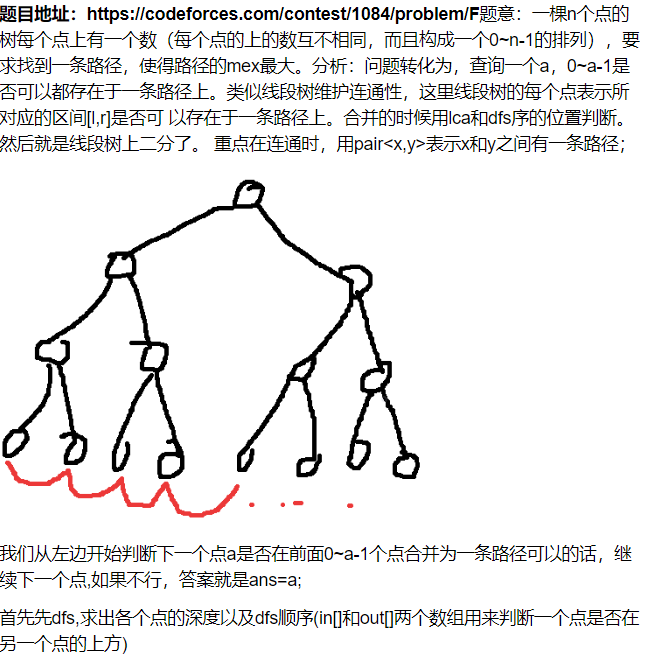
然后合并时注意分情况讨论：

---

参考代码：

 #include<bits/stdc++.h>
 using namespace std;
 #define pb push_back
 #define mkp make_pair
 #define fi first
 #define se second
 typedef long long ll;
 typedef pair<int,int> PII;
 const int INF=0x3f3f3f3f;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-') f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x*f;
 }
 const int maxn=2e5+;
 int n,q,typ,x,y,cnt,ans;
 int a[maxn],in[maxn],out[maxn];
 int dep[maxn],fc[],fa[][maxn];
 vector<int> G[maxn];
 PII res;

 inline void dfs(int u)
 {
     in[u]=++cnt;
     for(int i=;fc[i]<=dep[u];++i) fa[i][u]=fa[i-][fa[i-][u]];
     for(int i=,len=G[u].size();i<len;++i)
     {
         dep[G[u][i]]=dep[u]+;fa[][G[u][i]]=u;
         dfs(G[u][i]);
     }
     out[u]=++cnt;
 }

 inline int LCA(int x,int y)
 {
     if(dep[x]<dep[y]) swap(x,y);
     for(int i=,t=dep[x]-dep[y];t;++i)
         if(t&fc[i]) x=fa[i][x],t^=fc[i];
     for(int i=;~i;--i) if(fa[i][x]^fa[i][y])
         x=fa[i][x],y=fa[i][y];
     return x==y? x:fa[][x];
 }

 namespace Segment
 {
     #define ls (rt<<1)
     #define rs (rt<<1|1)
     PII T[maxn<<];

     bool anc(int x,int y){return in[x]<=in[y]&&out[x]>=out[y];}

     PII check(PII x,int y)
     {
         if(!x.fi || !y) return mkp(,);
         if(anc(x.fi,x.se)) swap(x.fi,x.se);
         if(anc(x.se,x.fi))
         {
             if(anc(x.fi,y)) return mkp(y,x.se);
             if(anc(x.se,y))
             {
                 if(anc(y,x.fi)) return x;
                 if(LCA(x.fi,y)==x.se) return mkp(x.fi,y);
                 return mkp(,);
             }
             return mkp(y,x.fi);
         }

         if(anc(x.fi,y)) return mkp(y,x.se);
         if(anc(x.se,y)) return mkp(x.fi,y);
         if(!anc(LCA(x.fi,x.se),y)) return mkp(,);
         if(!anc(y,x.fi) && !anc(y,x.se)) return mkp(,);
         return x;
     }

     PII merge(PII x,PII y)
     {
         if(x.fi==-) return y;
         x=check(x,y.fi);x=check(x,y.se);
         return x;
     }

     void update(int rt,int l,int r,int pos,int x)
     {
         if(l==r){T[rt]=mkp(x,x);return ;}
         int mid=l+r>>;
         if(pos<=mid) update(ls,l,mid,pos,x);
         else update(rs,mid+,r,pos,x);
         T[rt]=merge(T[ls],T[rs]);
     }

     bool query(int rt,int l,int r)
     {
         PII tmp=merge(res,T[rt]);
         if(tmp.fi){res=tmp;ans=r;return true;}
         if(l==r) return false;//
         int mid=l+r>>;
         if(query(ls,l,mid)) query(rs,mid+,r);
         return false;
     }
 }
 using namespace Segment;

 int main()
 {
     n=read(); fc[]=;
     for(int i=;i<=n;++i) a[i]=read()+;
     for(int i=;i<=n;++i) G[read()].pb(i);
     for(int i=;i<=;++i) fc[i]=fc[i-]<<;
     dfs();
     for(int i=;i<=n;++i) update(,,n,a[i],i);
     q=read();
     while(q--)
     {
         typ=read();
         if(typ==)
         {
             x=read();y=read();swap(a[x],a[y]);
             update(,,n,a[x],x);update(,,n,a[y],y);
         }
         else
         {
             res=mkp(-,);ans=;query(,,n);
             printf("%d\n",ans);
         }
     }

     return ;
 }

;