WebGL学习笔记（二）：WebGL坐标系及基础几何概念

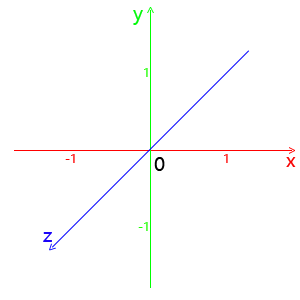
WebGL使用的是正交右手坐标系，且每个方向都有可使用的值的区间，超出该矩形区间的图像不会绘制：

• x轴最左边为-1，最右边为1；
• y轴最下边为-1，最上边为1；
• z轴朝向你的方向最大值为1，远离你的方向最大值为-1；

注：这些值与Canvas的尺寸无关，无论Canvas的长宽比是多少，WebGL的区间值都是一致的。

如图：

向量

点积

p1.x * p2.x + p1.y * p2.y + p1.z * p2.z

两个向量的分量相乘之后再相加的结果，该结果和两个向量的夹角相关；两个向量的点积为0时，表示这两个向量的夹角为90度，即相互垂直或正交，大于0时，表示夹角小于90度，小于0时，表示夹角大于90度；

叉乘

叉乘之后的结果不是一个标量，而是一个新的向量，该结果向量和用来运算叉乘的两个向量所在的平面垂直；该向量即三角形平面的法向量；

齐次坐标

我们表示一个3维空间的向量或点时，一般使用包含3个分量的Vector3来表示，而齐次坐标则多引入了一个分量；

之所以多引入一个分量，是为了在仿射变换中的运算更加的方便，更具体的解说请看下面的文章：

https://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html

https://blog.csdn.net/janestar/article/details/44244849

矩阵

在3D中，一般使用4x4的矩阵。

相乘

矩阵相乘在3D图形中是一个非常重要的运算，在3D中无论是移动、旋转还是缩放大小，都是通过在当前矩阵的基础上乘以一个新的矩阵来达到目的。

单位矩阵

可以理解为常量中的1，任何矩阵乘于单位矩阵都不变。

逆矩阵

逆矩阵可以理解为倒数，即当前矩阵乘于其逆矩阵的结果为单位矩阵，需要注意的是，只有方阵（行列数量相等）才有逆矩阵，同时不是所有的方阵都有逆矩阵。

引入逆矩阵的原因之一是用来实现矩阵的除法。比如有矩阵X，A，B，其中X*A = B，我们要求X矩阵的值。本能来说，我们只需要将B/A就可以得到X矩阵了。但是对于矩阵来说，不存在直接相除的概念。我们需要借助逆矩阵，间接实现矩阵的除法。具体的做法是等式两边在相同位置同时乘以矩阵A的逆矩阵，如下所示，X*A*（A的逆矩阵）=B*（A的逆矩阵）。由于A*（A的逆矩阵）=I，即单位矩阵，任何矩阵乘以单位矩阵的结果都是其本身。所以，我们可以得到X=B*（A的逆矩阵）。

转置矩阵

转置矩阵是指将行列互换之后的矩阵，和逆矩阵常用于法线变换。

仿射变换

矩阵的仿射变换包含了主要包含了平移、旋转和缩放。