洛谷 P5057 [CQOI2006]简单题 题解

P5057 [CQOI2006]简单题

题目描述

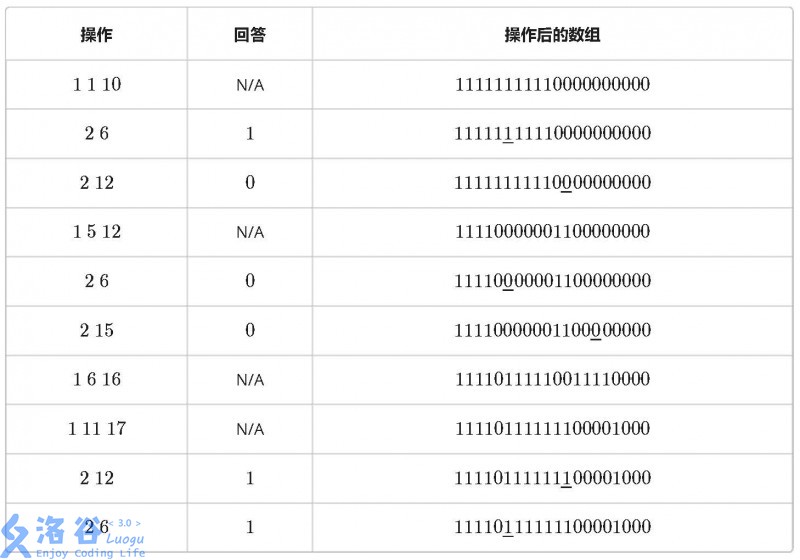
有一个 n 个元素的数组，每个元素初始均为 0。有 m 条指令，要么让其中一段连续序列数字反转——0 变 1，1 变 0（操作 1），要么询问某个元素的值（操作 2）。 例如当 n = 20 时，10 条指令如下：

输入格式

第一行包含两个整数 n, m，表示数组的长度和指令的条数； 以下 m 行，每行的第一个数 t 表示操作的种类：

若 t = 1，则接下来有两个数 L, R，表示区间 [L, R] 的每个数均反转； 若 t = 2，则接下来只有一个数 i，表示询问的下标。

输出格式

每个操作 2 输出一行（非 0 即 1），表示每次操作 2 的回答。

输入输出样例

输入 #1

20 10

1 1 10

2 6

2 12

1 5 12

2 6

2 15

1 6 16

1 11 17

2 12

2 6

输出 #1

1

0

0

0

1

1

说明/提示

对于 50% 的数据，\(1 ≤ n ≤ 10^3\),$ 1 ≤ m ≤ 10^4$； 对于 100% 的数据，\(1 ≤ n ≤ 10^5\), \(1 ≤ m ≤ 5 × 10^5\)，保证 L ≤ R。

【树状数组】

【思路】

树状数组

【题目大意】

区间反转和单点询问

【题目分析】

区间反转我首先想到了是线段树

用lazy标记某个区间反转过几次

但是我是抱着练习树状数组的目的

来做的这道题

所以必须用树状数组做!!!

不过树状数组该怎么办呢？

难不成枚举每一个点然后修改？

不对

这个时候情不自禁想到了那个优美的东西

差分

类似树状数组模板2的方法

差分一下下就可以很轻松标记翻转次数了

【核心思路】

树状数组维护差分数组

差分数组修改区间

只需要在区间左端点加上修改的值

在右端点之后减去修改的值就好了

求某个位置上的值

就是这个位置之前（包括这个位置）的和

也符合树状数组里面的sum

就不需要做差了

最后按照%2来输出就好了

因为翻转两次之后会回到原来的情况

【思路】

#include<iostream>
#include<cstdio>
#define int long long
using namespace std;
const int Max = 100006;
int a[Max];
int n,m;
int read()
{
	int sum = 0,fg = 1;
	char c = getchar();
	while(c < '0' || c > '9')
	{
		if(c == '-')fg = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9')
	{
		sum = sum * 10 + c - '0';
		c = getchar();
	}
	return sum * fg;
}

int lowbit(int x)
{
	return x & -x;
}

void add(int x,int y)
{
	while(x <= n)
	{
		a[x] += y;
		x += lowbit(x);
	}
}

int sum(int x)
{
	int ans = 0;
	while(x > 0)
	{
		ans += a[x];
		x -= lowbit(x);
	}
	return ans;
}

signed main()
{
	n = read(),m = read();
	for(register int i = 1;i <= m;++ i)
	{
		int t = read();
		if(t == 1)
		{
			int l = read(),r = read();
			add(l,1);
			add(r + 1,-1);
		}
		else
		{
			int qwq = read();
			cout << sum(qwq) % 2 << endl;
		}
	}
	return 0;
}

【线段树】

【思路】

线段树

首先感谢@大魔鬼灿灿 巨佬帮我滑鼠标

用树状数组做过了，但是还是可以用线段树做的

所以也拿线段树来做回顾一下线段树，

然后没想到调试了两个小时

【核心思路】

sum记录这个点被修改的次数

因为是区间修改和单点查询

所以线段树中只要不是叶子节点的sum就不需要求了

只用来lazy标记就可以了

然后该下放到叶子节点的时候就下发好了

最后输出记录的修改次数%2

【注意事项】

不管不是叶子节点的sum没问题

但是有的修改的时候却是单点修改

所以该sum++还是得sum++的

把全部节点的sum都当叶子节点的来处理

加上修改的次数

也就是lazy值就好了

【完整代码】

#include<iostream>
#include<cstdio>
#define lson (k << 1)
#define rson (k << 1 | 1)

using namespace std;

int read()
{
	int sum = 0,fg = 1;
	char c = getchar();
	while(c < '0' || c > '9'){if(c == '-')fg = -1;c = getchar();}
	while(c >= '0' && c <= '9'){sum = sum * 10 + c - '0';c = getchar();}
	return sum * fg;
}
const int Max = 100004;
struct node
{
	int l,r;
	int lazy;
	int sum;
}a[Max << 2];
int n,m;
int opx,opl,opr;

void build(int k,int l,int r)
{
	a[k].l = l;a[k].r = r;
	if(l == r)
		return;
	int mid = (l + r) >> 1;
	build(lson,l,mid);
	build(rson,mid + 1,r);
	return;
}

void down(int k)
{
	if(a[k].lazy)
	{
		a[lson].sum += a[k].lazy;
		a[rson].sum += a[k].lazy;
		a[lson].lazy += a[k].lazy;
		a[rson].lazy += a[k].lazy;
		a[k].lazy = 0;
	}
}

void change(int k)
{
	if(opl <= a[k].l && opr >= a[k].r)
	{
		a[k].lazy ++;
        a[k].sum++;
		return;
	}
	down(k);
	int mid = (a[k].l + a[k].r) >> 1;
	if(opl <= mid)change(lson);
	if(opr > mid)change(rson);
	a[k].sum = a[lson].sum + a[rson].sum;
}

void query(int k)
{
	if(a[k].l == opx && a[k].r == opx)
	{
		cout << a[k].sum % 2 << endl;
        return;
	}
	down(k);
	int mid = (a[k].l + a[k].r) >> 1;
	if(opx <= mid) query(lson);
	if(opx > mid) query(rson);
}

int main()
{
	n = read(),m = read();
	build(1,1,n);
	for(register int i = 1;i <= m;++ i)
	{
		int qwq = read();
		if(qwq == 1)
		{
			opl = read(),opr = read();
			change(1);
		}
		else
		{
			opx = read();query(1);
		}
	}
	return 0;
}