2553 ACM N皇后 回溯递归

题目：http://acm.hdu.edu.cn/showproblem.php?pid=2553
中文题目，题意很简单。
思路：听说这是学习递归的经典题目，就来试试，发现自己一点想法都没有，一遇到递归，就懵逼。于是看了别人的代码，自己一步一步的看了几遍，然后自己又敲了一遍。对回溯递归有了新的认识。
由题意可知，每一行有且仅有一颗棋子，curRow代表当前将要下棋的行数。下棋是一行一行的遍历，下完，再遍历下一行，每次下棋都要看是否符合题意：1，不能与其他棋子同行或同列，不能和其他棋子是对角线。所以就要对以及下棋的0到curRow-1行与第curRow行棋子比较。左对角线（行数-列数相等），右对角线（行数+列数相等）。
EG：n=3

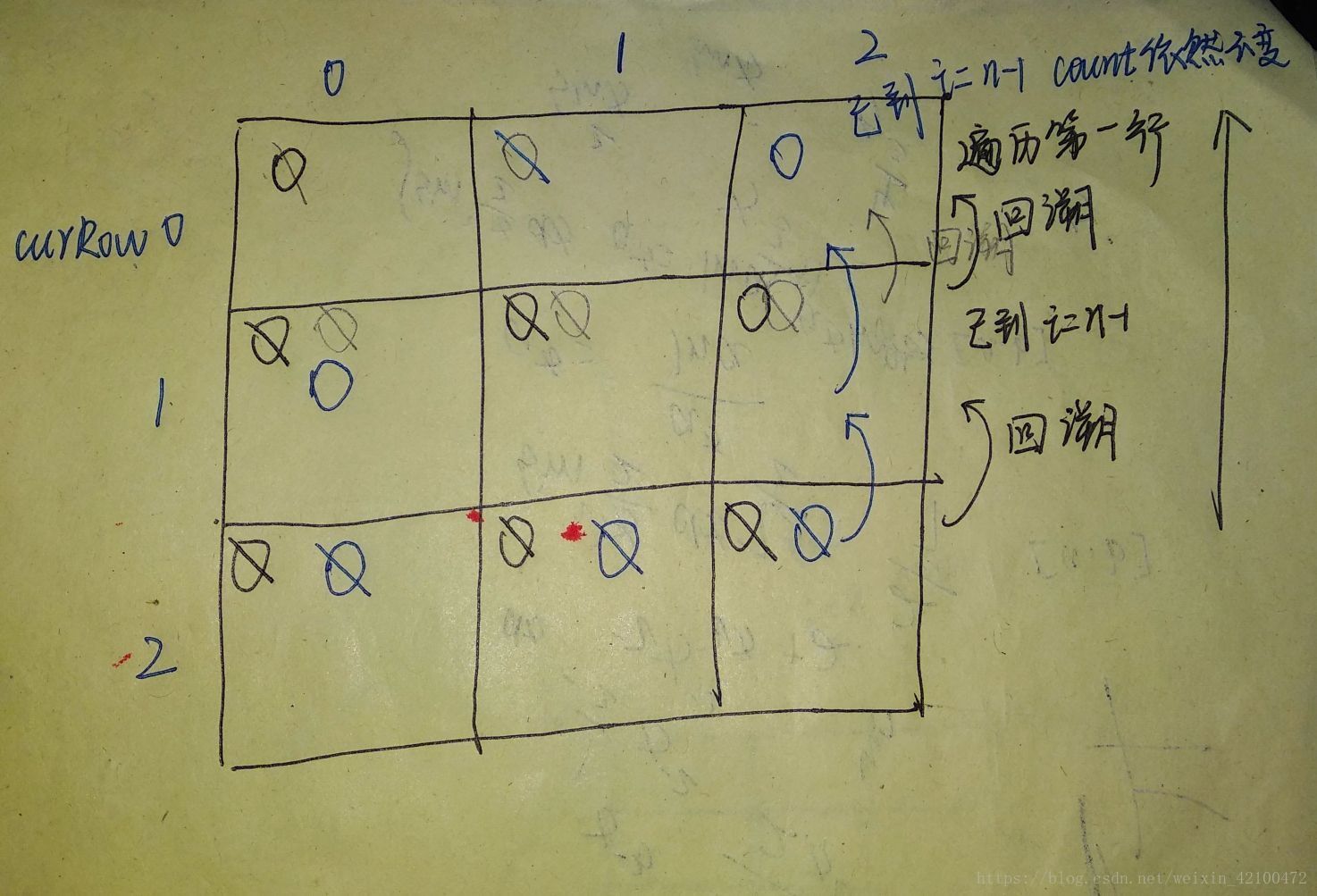
先是黑笔->铅笔->蓝笔

#include<stdio.h>
int row[11],count,N;//全局变量，不用单独传值
void search(int curRow)
{
    int i,j;
    if(curRow==N)
        count++;
    else
        for(i=0;i<N;i++)
        {
            row[curRow]=i;
            int ok=1;//找到符合题意的一局棋。
            for(j=0;j<curRow;j++)
                if(row[curRow]==row[j]||curRow-row[curRow]==j-row[j]||curRow+row[curRow]==j+row[j])
                {
                    ok=0;
                    break;
                }//一旦if条件成立，舍弃当前棋子，然后先在同一行中，选择下一列，如果同一行
                //每一列都不符合题意，那么回溯。
                if(ok)
                    search(curRow+1);//遍历下一行
        }
}
int main()
{
    int num[11];//从1开始记数，题意是1开始的。
    for(int i=1;i<=10;i++)
    {
        N=i;
        search(0);
        num[i]=count;
        count=0;
    }
    while(scanf("%d",&N)!=EOF&&N)
        printf("%d\n",num[N]);
}