Within K stops 最短路径 Cheapest Flights Within K Stops

2018-09-19 22:34:28

问题描述：

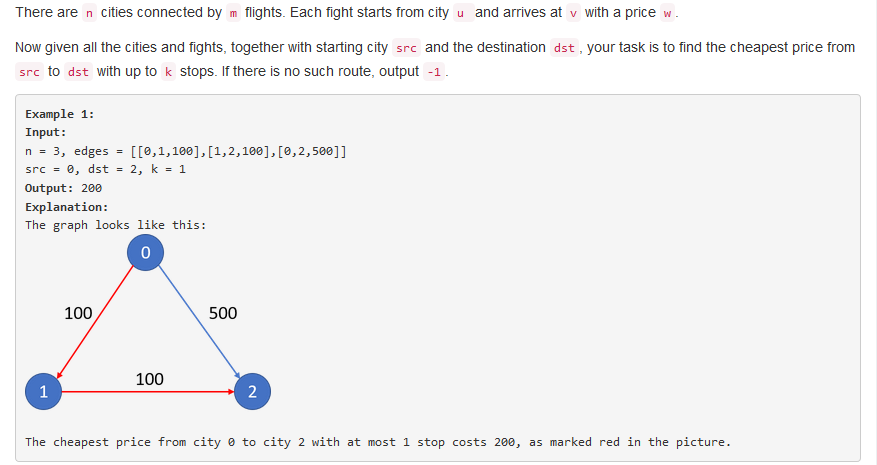
问题求解：

本题是典型的最短路径的扩展题，可以使用Bellman Ford算法进行求解，需要注意的是在Bellman Ford算法的时候需要额外申请一个数组来保存变量。

    int inf = (int)1e9;
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {
        // write your code here
        int[] dist = new int[n];
        Arrays.fill(dist, inf);
        dist[src] = 0;
        for (int i = 0; i <= K; i++) {
            int[] prev = Arrays.copyOf(dist, n);
            for (int[] e : flights) {
                int from = e[0];
                int to = e[1];
                int w = e[2];
                if (prev[to] > prev[from] + w) {
                    dist[to] = prev[from] + w;
                }
            }
        }
        return dist[dst] == inf ? -1 : dist[dst];
    }