洛谷 P4515 [COCI2009-2010#6] XOR

题意

平面直角坐标系中有一些等腰直角三角形，且直角边平行于坐标轴，直角顶点在右下方，求奇数次被覆盖的面积。N<=10。输入为x,y,r，分别表示三角形顶点的坐标与三角形的边长。

如：

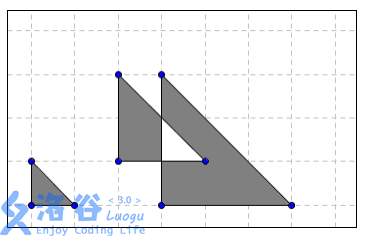总面积为0.5+2+4.5-0.5-0.5=6

---

思考

看到数据范围，就肯定是优美的暴力。

这题思路很清奇。首先我们要先求出任意几个三角形面积的交，但我们知道两个之间的关系就行了，因为这样特殊的三角形最后的交必然一模一样（只是缩放了）。

为了算出面积的交，我们先考虑算出最后交的三角形的边长，因为这样子平方一下除以二就是面积。

我们还知道，交的边长关于x,y,r一定是一次关系，至少是只有一次项，而且没有常数。我们不妨考虑这些三角形的y都相等。

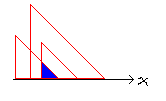如图，这种情况下的边长为max{0,min{xi+ri}-max{xi}}，即若有交，x+r一定要最小，这样所有三角形才能够到，再减去x最大的一个。若没交，不难证明结果小于0。

同样地，x都相等时边长为max{0,min{yi+ri}-max{yi}}，于是我们考虑合并起来。

经过打表（即我不会证明），我们发现最后的结果为max{0,min{xi+yi+ri}-max{xi}-max{yi}}。

这样完成了第一步。然后容斥考虑面积并。看看每个重叠的三角形对答案的贡献：

不难发现，若有n个三角形重叠，则数量上的贡献为(-2)^(n-1)，具体证明归纳法。

dfs一下即可。

代码

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long int ll;
 const ll maxn=;
 const ll inf=INT_MAX;
 ll max(ll x,ll y){return x>y?x:y;}
 ll x[maxn],y[maxn],r[maxn],n,ans;
 void dfs(ll s,ll maxx,ll maxy,ll maxc,ll g)
 {
     if(s==n+)
     {
         if(g>=)ans+=pow(-,g-)*max(,maxc-maxx-maxy)*max(,maxc-maxx-maxy);
         return;
     }
     dfs(s+,maxx,maxy,maxc,g);
     dfs(s+,max(maxx,x[s]),max(maxy,y[s]),min(maxc,x[s]+y[s]+r[s]),g+);
 }
 int main()
 {
     ios::sync_with_stdio(false);
     cin>>n;
     for(int i=;i<=n;++i)cin>>x[i]>>y[i]>>r[i];
     dfs(,,,inf,);
     cout<<fixed<<setprecision()<<double(ans)/<<endl;
     return ;
 }