POJ-2411 Mondriann's Dream (状压DP)

求把\(N*M(1\le N,M \le 11)\) 的棋盘分割成若干个\(1\times 2\) 的长方形，有多少种方案。例如当 \(N=2,M=4\)时，共有5种方案。当\(N=2,M=3\)时，有3种方案。

NM只有11，八九不离十可以状压了，反正得挨个铺，所以从上到下考虑。假如现在铺好了前\(i\) 层，基本思想就是从\(i\) 层的状态转移到\(i+1\)层的状态。但是该如何表示？观察一下铺满第 \(i\) 层的样子（必须保证第\(i\)层是满的，也就是说有的可以凸出来到\(i+1\)层但是要保证\(i\)层是满的）

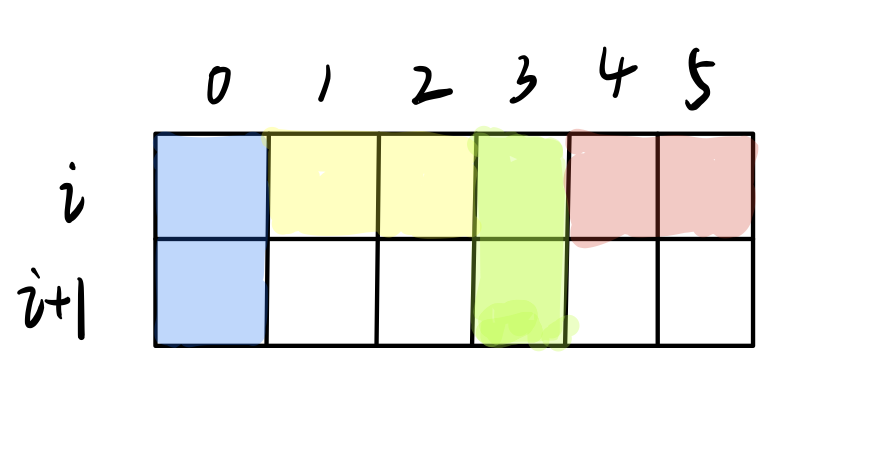
对于第 i 行中竖着放的，第 \(i+1\) 层要受到牵连，它必须补全竖着放置的上一半才行。但对于横着放的，第\(i+1\)层则无所谓。

所以我们可以用二进制中的 1 来表示他是否是竖着放置的上一半。为0则为其他状况。

\(d[i][j]\)表示第 \(i\) 的形态为\(j\) 时，前\(i\) 行分割方案的总数。 \(j\) 是用十进制整数记录的 \(m\) 位二进制数。考虑\(i+1\)行的状态\(k\)在满足什么情况下转移是合法的。

• \(j\)中为 1 的位，\(k\)中必须为0
• \(j\)中为 0 的位，\(k\)中可以为1，但 k 要是为 0，就必须是连续的偶数个0（想一想为什么)
  
  对于第一条，可以用 \(i\&j = 0\) 来判断，对于第二条，有\(z = i|j\)，那么 z 的二进制表示中，每一段连续的 0 都必须有偶数个。（这些0代表若干个横着的 \(1\times 2\) 长方形，奇数个0无法分割成这种形态。

#include <iostream>
#include <cstdio>
using namespace std;
int n,m;
long long f[12][1<<11];
bool in_s[1<<11];

int main(){
    while(cin>>n>>m && n){
        //先把合法状态筛出来，即二进制表示中每一段连续的0都有偶数个
        for(int i=0;i<1<<m;i++){
            bool cnt = 0,has_odd = 0;
            for(int j=0;j<m;j++)
                if(i >> j & 1)has_odd |= cnt,cnt=0;
                else cnt ^= 1;
            in_s[i] = (has_odd | cnt) ? 0 : 1;
        }
        f[0][0] = 1;
        for(int i=1;i<=n;i++){
            for(int j=0;j<1<<m;j++){
                f[i][j] = 0;
                for(int k=0;k< 1<<m;k++){
                    if((j & k) == 0 && in_s[j|k])
                        f[i][j] += f[i-1][k];
                }
            }
        }
        cout<<f[n][0]<<endl;
    }
    return 0;
}