C++实现二叉树的基本操作：建立、遍历、计算深度、节点数、叶子数等

题意：



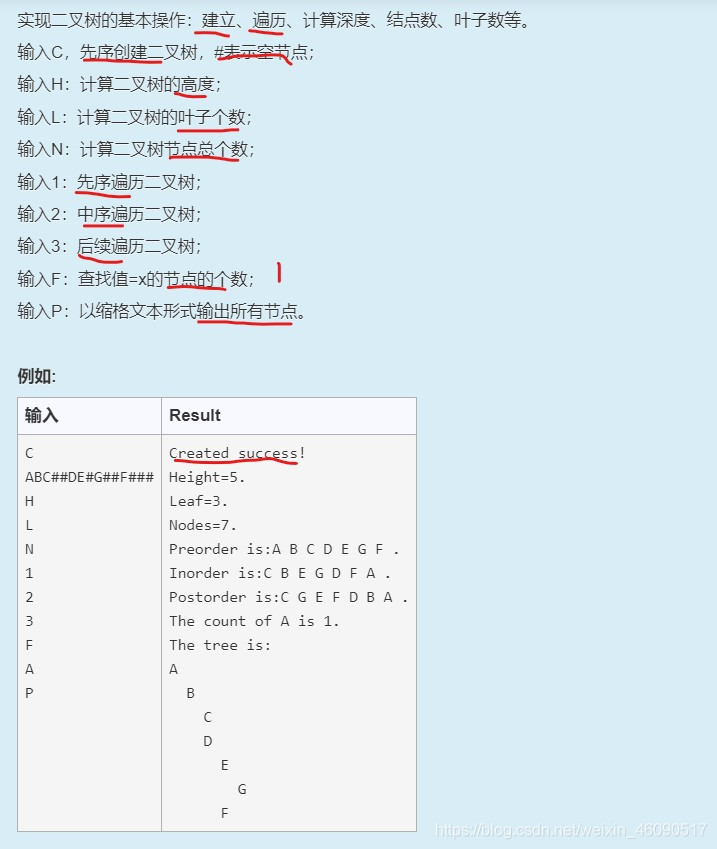
代码实现：

#include<iostream>
#include<queue>
#include<stack>

using namespace std;

//二叉树节点
struct BinaryTreeNode
{
    char data;
    BinaryTreeNode* leftChild;
    BinaryTreeNode* rightChild;
};
//堆栈节点，用于深度遍历
struct stackNode
{
    BinaryTreeNode* ptr;
    char tag;//tag=0标志进入左子树，tag=1标志进入右子树
};

class BinaryTree //二叉树的类
{
public:
//根据完全前序遍历创建二叉树
    void createBinaryTree(BinaryTreeNode* &root)
    {
        root=new BinaryTreeNode();
        char newData;
        cin>>newData;
        if(newData=='#')
        {
            root=NULL;
        }
        else
        {
            root->data=newData;
            createBinaryTree(root->leftChild);
            createBinaryTree(root->rightChild);
        }
    }
//递归实现前序遍历
    void preTraversal(BinaryTreeNode* root)
    {
        if(root!=NULL)
        {
            cout<<root->data<<" ";
            preTraversal(root->leftChild);
            preTraversal(root->rightChild);
        }
    }

//递归实现后续遍历
    void lastTraversal(BinaryTreeNode* root)
    {
        if(root!=NULL)
        {
            lastTraversal(root->leftChild);
            lastTraversal(root->rightChild);
            cout<<root->data<<" ";
        }
    }

//非递归实现中序遍历
    void mid(BinaryTreeNode* root)
    {
        stack<BinaryTreeNode*> S;
        BinaryTreeNode* p=root;
        do
        {
            while(p!=NULL)
            {
                S.push(p);
                p=p->leftChild;
            }
            if(!S.empty())
            {
                p=S.top();
                cout<<p->data<<" ";
                S.pop();
                p=p->rightChild;
            }
        }
        while(p!=NULL||!S.empty());
    }

//计算节点总数
    int nodeCount(BinaryTreeNode* &root)
    {
        if(root==NULL)
        {
            return 0;
        }
        else
        {
            return nodeCount(root->leftChild)+nodeCount(root->rightChild)+1;
        }
    }
//计算二叉树的高度
    int treeHight(BinaryTreeNode* &root)
    {
        if(root==NULL)
        {
            return 0;
        }
        else
        {
            int LH=treeHight(root->leftChild);
            int RH=treeHight(root->rightChild);
            return LH > RH ? LH+1 : RH+1;
        }
    }
//计算二叉树的叶子个数
    int getLeavesCount(BinaryTreeNode* &root)
    {
        if(root==NULL)
        {
            return 0;
        }
        else if (root->leftChild == NULL && root->rightChild == NULL)
        {
            return 1;
        }
        else
        {
            int leftLeavesCount = getLeavesCount(root->leftChild);
            int rightLeavesCount = getLeavesCount(root->rightChild);
            return leftLeavesCount + rightLeavesCount;
        }
    }
//查找值=x的节点个数
    int findNode(BinaryTreeNode* &root,char x,int coun)
    {

        if(root!=NULL)
        {
            if(root->data==x) coun++;
            findNode(root->leftChild,x,coun);
            findNode(root->rightChild,x,coun);
        }
        return coun;
    }
//以缩格文本形式输出所有节点
    void outputNode(BinaryTreeNode* &root,int x)
    {
        if(root!=NULL)
        {
            for(int i=0;i<x;i++) cout<<" ";
            cout<<root->data<<endl;
            x=x+2;
            outputNode(root->leftChild,x);
            outputNode(root->rightChild,x);
        }

    }

};

int main()
{
    BinaryTree tree;
    BinaryTreeNode* treeRoot;
    char func;
    while(cin>>func){
        if(func=='C')
        {
            tree.createBinaryTree(treeRoot);
            cout<<"Created success!";
        }
        if(func=='1') {cout<<"Preorder is:";tree.preTraversal(treeRoot);cout<<".";}
        if(func=='2') {cout<<"Inorder is:";tree.mid(treeRoot);cout<<".";}
        if(func=='3') {cout<<"Postorder is:";tree.lastTraversal(treeRoot);cout<<".";}
        if(func=='N') cout<<"Nodes="<<tree.nodeCount(treeRoot)<<".";
        if(func=='H') cout<<"Height="<<tree.treeHight(treeRoot)<<".";
        if(func=='L') cout<<"Leaf="<<tree.getLeavesCount(treeRoot)<<".";
        if(func=='F')
        {
            char x;
            cin>>x;
            cout<<"The count of "<<x<<" is "<<tree.findNode(treeRoot,x,0)<<".";
        }
        if(func=='P')
        {
            cout<<"The tree is:"<<endl;
            tree.outputNode(treeRoot,0);
        }
        cout<<endl;
    }

    return 0;
}

PS：有时间再补充注意点吧