深度优先搜索算法（Depth-First-Search，DFS）

深度优先搜索算法的概念

　　与广度优先搜索算法不同，深度优先搜索算法类似与树的先序遍历。这种搜索算法所遵循的搜索策略是尽可能“深”地搜索一个图。它的基本思想如下：首先访问图中某一个起始顶点v，然后由v出发，访问与v相邻且未被访问的任一顶点w1,再访问与w1邻接且未被访问的任一顶点w2，….重复上述过程。当不能再继续向下访问时，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直到图中所有顶点均被访问过为止

(举个例子，从你开始遍历你的所有亲戚，例如：先访问你的儿子，再从你的儿子继续访问你的儿子的儿子，直到你的儿子是最后一个顶点，再回退回上一层，访问你儿子的女儿，再访问你儿子的女儿的儿子….依此类推，直到你的所有亲戚都被访问过一次为止，这和广度优先搜索的算法区别还是很大的)。

　　

算法伪代码

　　DFS采用的是递归的过程，所以这个过程需要一个递归工作的辅助栈，伪代码如下：

　　

bool visited[MAX_VERTEX_NUM];//访问标记数组

void DFSTraverse(Graph G){

//对图G进行深度优先遍历，访问函数为visit（）

    for(v=0;v<G.vexnum;++i)

        visited[v]=false;//初始化所有顶点的数据，false表示未曾访问过

    for(v=0;v<G.vexnum;++v)

        if(!visited[v])

            DFS(G,v);//这里从0遍历到最后一个顶点是为了防止有极端情况出现：

                     //可能存在顶点wi无法从顶点w0遍历到，所以需要对它也调用一次DFS算法

}

void DFS(Graph G,int v){

//从顶点v出发，采用递归的思想，深度优先遍历图G

    visit（v）;//访问顶点v

    visited[v]=true;//设置这个顶点为已经访问过

    for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))

        if(!visited[w])

            DFS(G,w);//递归调用查找第一个未被访问的邻接顶点

}

实例及分析

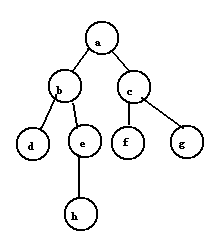
　　深度优先遍历

　　首先访问a，并置a为已经访问；然后访问与a邻接且未被访问的顶点b，置b为已经访问，然后访问与b邻接且未被访问的顶点d，置d为已经访问。此时d已经没有未被访问过的邻接点，这时候返回上一个访问过的顶点b，访问与其邻接且未被访问的顶点e，置e为已经访问……。依此类推，直到途中所有的顶点都被访问一次且仅仅被访问一次，遍历结果为abdehcfg。

DFS算法的性能分析

　　DFS算法是一个递归算法，需要借助一个递归工作栈，所以它的空间复杂度是O(|V|)。

　　遍历图的过程实际上是对每个顶点查找其邻接点的过程，其耗费的时间取决于所采用的存储结构，当以邻接矩阵表示时，查找每个顶点的临界点所需时间为O（|V|），故总的时间复杂度为O(|V|²)。当以邻接表表示时，查找所有顶点的邻接点所需时间为O(|E|)，访问顶点所需时间为O(|V|),此时，总的时间复杂度为O(|V|+|E|)。