HDU3507Print Article （斜率优化DP）

Zero has an old printer that doesn't work well sometimes. As it is antique, he still like to use it to print articles. But it is too old to work for a long time and it will certainly wear and tear, so Zero use a cost to evaluate this degree. 
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost 

M is a const number. 
Now Zero want to know the minimum cost in order to arrange the article perfectly. 

InputThere are many test cases. For each test case, There are two numbers N and M in the first line (0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000). Then, there are N numbers in the next 2 to N + 1 lines. Input are terminated by EOF.OutputA single number, meaning the mininum cost to print the article.Sample Input

5 5
5
9
5
7
5

Sample Output

230

应该是初步get了，由于以前看到的博主的配图和用语有误，让人再混沌之中浮尸了好久，头疼，应该是这样的图。

wa，我自己画的，将就辣。

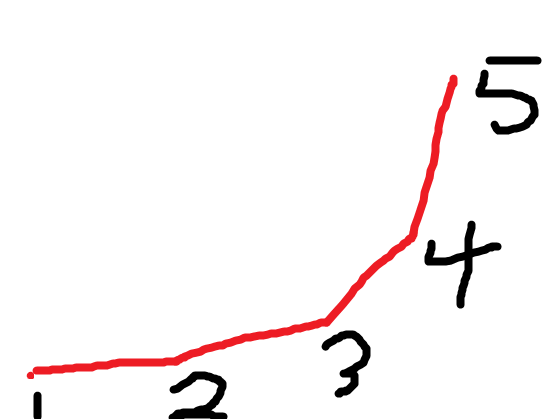
开始学的时候感觉好抽象啊，还特意去学了瞎‘凸包’专题，QwQ，这里主要是解释一下‘为什么’。

初学感悟：

零：我们把线段的两个端点叫做点对，把dp[j]+(sum[i]-sum[j])^2取得最小的是j叫做i的最优点。

一：一对点对里，前面的点和后面的点的优劣关系由sum i决定，但是删去前劣后优的点后，剩下的就是前由后劣，得到i时的队首最优。

Ω，本来的点对满足k=（y1-y2）/(x1-x2) > sum[i]，由于sum i是递增的，后面这个不等关系可能会改变。即此时（i==n时）队首是最优点，但是当i>n时,可能存在k<sum[i]，这也是为什么我们需要每个i维护队首元素，使得队首是最优点。

二：我们维护的是一个斜率上升的图形，1,2,3,4代表的是队列里的点，求dp i时有4步：

α,  对队首：斜率k(1,2)和sum i 的关系不再得到满足，说明对于i点，队首1已经不如队首2优，抛弃1，依此后推...

β,  dp i= dp q[top]+...

γ,   对队尾：具体的如果我们要加入一点5，如果斜率k(4,5)<k(3,4)，4点被抛弃：不等式（yj-yk）/(xj-xk) <= sum[i]，由于sum i递增，此时小于等于，即删去的点对i不会最优，对后面的i+更不会...

ε,   i入队尾，由于删去γ中不满足的点后，加入后满足图像斜率依旧上升。

三：为什么i的最优值在队首取得？

ζ, 见一，删去前劣后优的点后，剩下的就是前由后劣，队首为最优点。

四：注意整理中要考虑下正负，涉及到不等号的方向，当然此题毋须多虑。

θ, 把除法转化成乘法；注意符号。

(写法是左开右闭)

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=;
int dp[maxn],sum[maxn],q[maxn];
int n,m;
int getdp(int i,int j)
{
    return dp[j]+(sum[i]-sum[j])*(sum[i]-sum[j])+m;
}
int getdy(int i,int j)
{
    return  dp[i]+sum[i]*sum[i]-dp[j]-sum[j]*sum[j];
}
int getdx(int i,int j)
{
    return *(sum[i]-sum[j]);
}
int main()
{
     int i,j,n,head,tail;
      while(~scanf("%d%d",&n,&m))
      {
            for(i=;i<=n;i++) scanf("%d",&sum[i]);
            for(i=;i<=n;i++) sum[i]+=sum[i-];
            head=tail=;q[]=;
            for(i=;i<=n;i++){
                while(head<tail&&(getdy(q[head+],q[head])<=sum[i]*getdx(q[head+],q[head]))) head++;
                dp[i]=getdp(i,q[head]);
                while(head<tail&&(getdy(i,q[tail])*getdx(i,q[tail-])<=(getdy(i,q[tail-])*getdx(i,q[tail])))) tail--;
                q[++tail]=i;
            }
            printf("%d\n",dp[n]);
     }
     return ;
}