矩池云上安装ikatago及远程链接教程

https://github.com/kinfkong/ikatago-resources/tree/master/dockerfiles

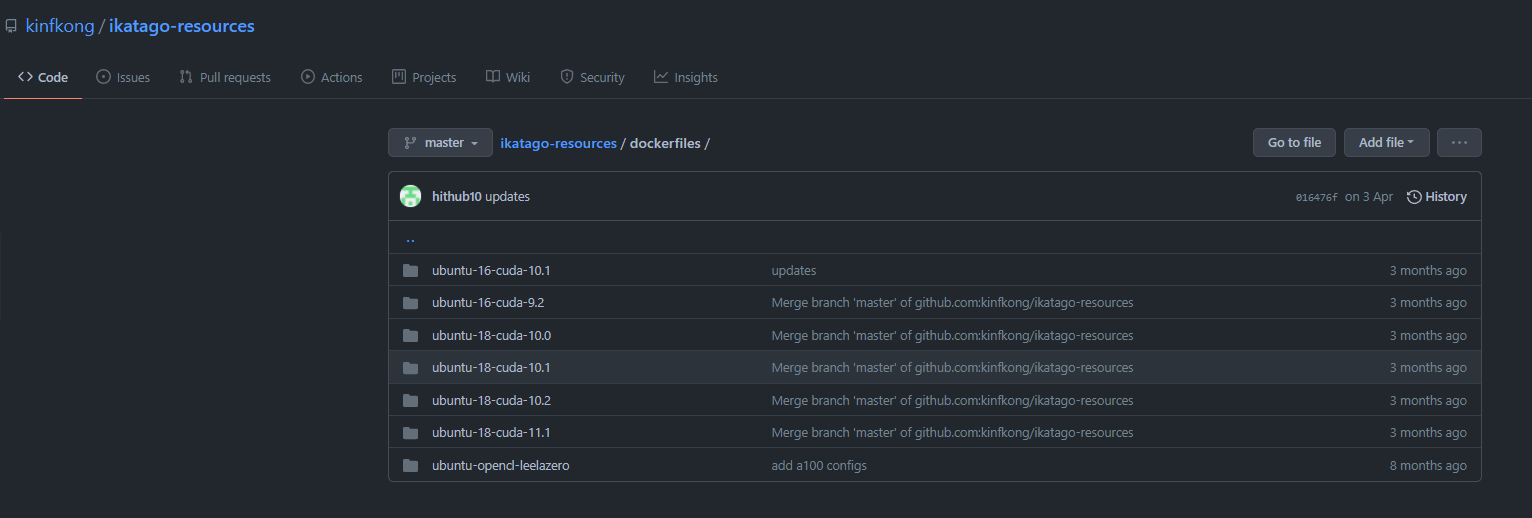
从作者的库中可以看到，该程序支持cuda9.2、cuda10、cuda10.1、cuda10.2、cuda11.1等镜像,矩池云上的镜像基本上都可以满足他的要求，可以任意选用。

案例：用的cuda10.2的镜像

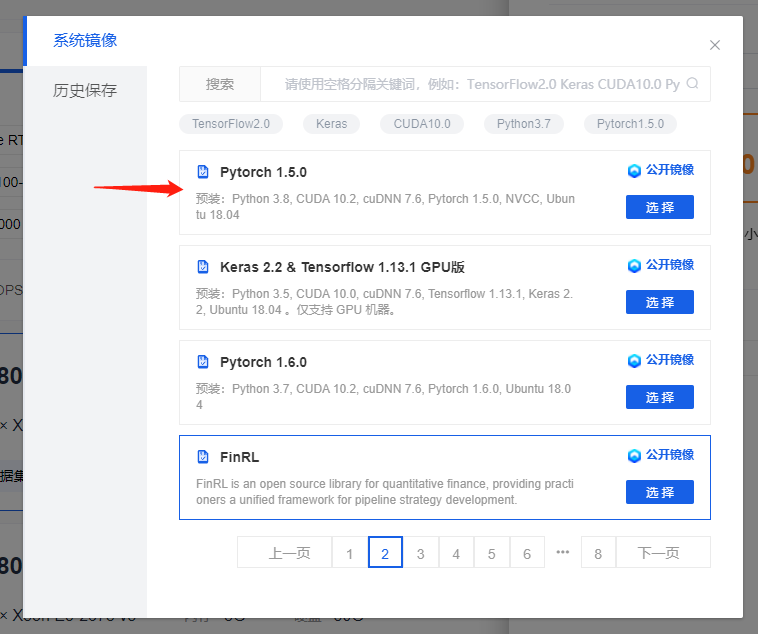
利用脚本安装

cd ~; /bin/bash -c "$(curl -fsSL https://ikatago-resources.oss-cn-beijing.aliyuncs.com/all/install.sh)"

如果报错“sh: curl: command not found”是没有curl，先安装一下。

apt-get update
apt install curl

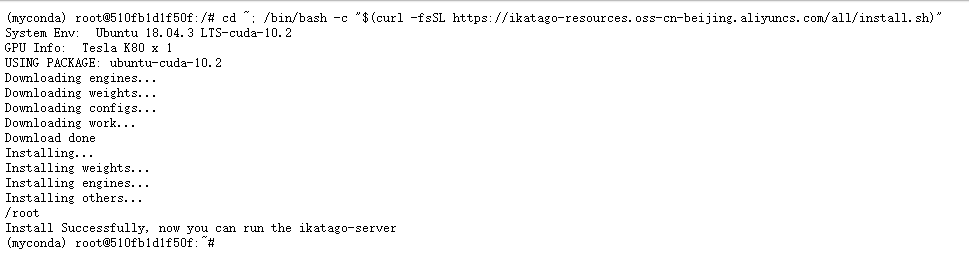
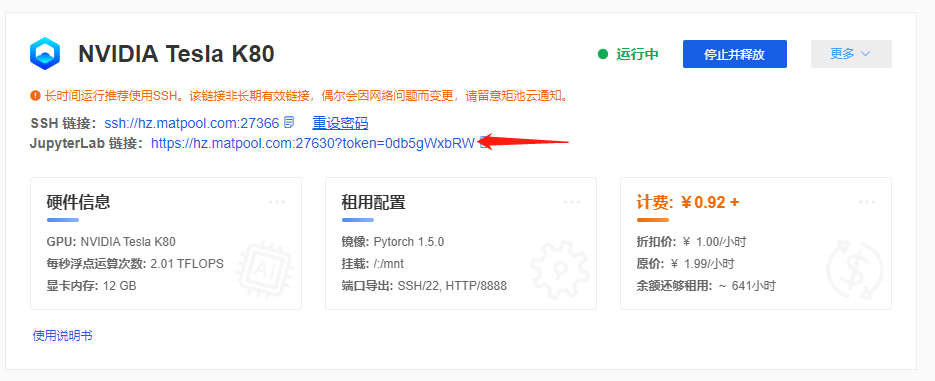
安装后，文件路径在root目录下的work文件夹内，文件有如下

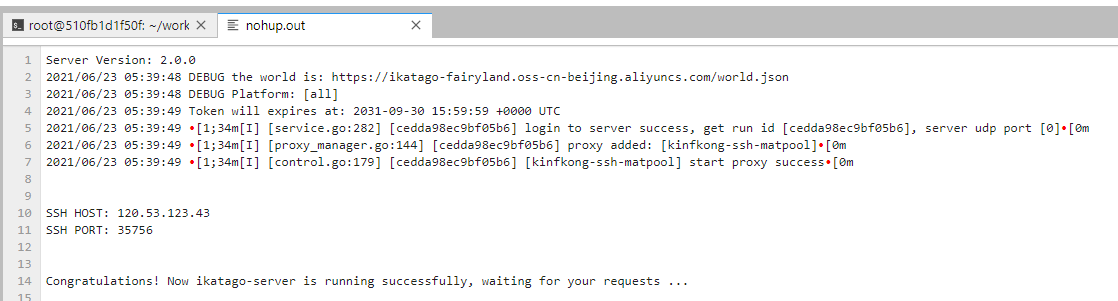
运行

运行命令:

cd ~/work; ./run.sh 你的用户名 你的密码

建议使用 挂后台运行命令:

cd ~/work; nohup ./run.sh 你的用户名 你的密码 &

密码建议使用复杂一些的密码，可以用生成工具生成，比如lastpass的password generator。

https://www.lastpass.com/password-generator

案例如下：

cd ~/work; nohup ./run.sh matpool sNoeoLSVDVrZ &

下载ikatago-client

https://github.com/kinfkong/ikatago-client

https://github.com/kinfkong/ikatago-client/releases/tag/1.3.3

直接下载

https://github.com/kinfkong/ikatago-client/releases/download/1.3.3/ikatago-1.3.3-win64.zip

下载Sabaki

https://github.com/SabakiHQ/Sabaki

https://github.com/SabakiHQ/Sabaki/releases/tag/v0.51.1

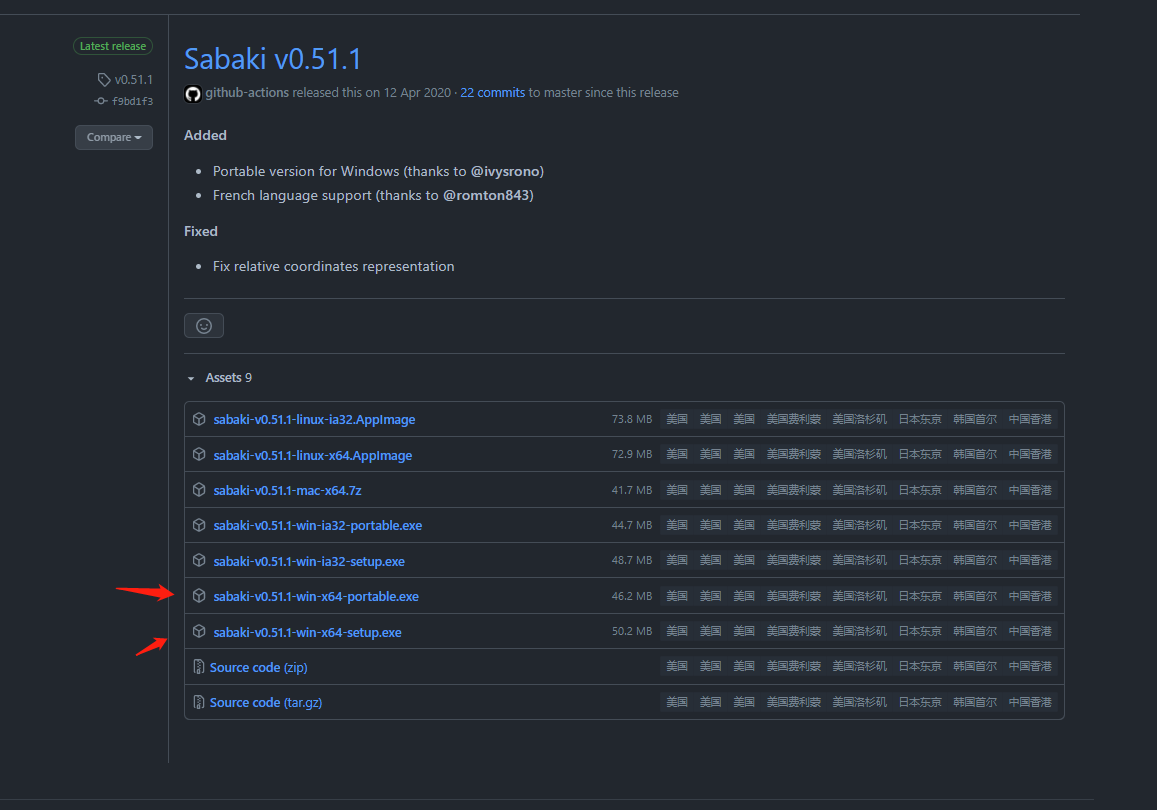
portable便携版

https://github.com/SabakiHQ/Sabaki/releases/download/v0.51.1/sabaki-v0.51.1-win-x64-portable.exe

安装版

https://github.com/SabakiHQ/Sabaki/releases/download/v0.51.1/sabaki-v0.51.1-win-x64-setup.exe

Sabaki配置

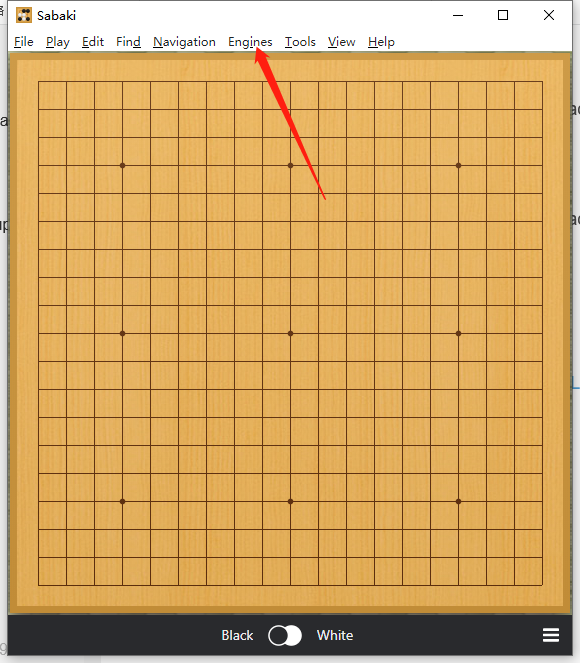
在菜单栏点击 Engines - Show Engines Sidebar 显示侧边引擎栏。

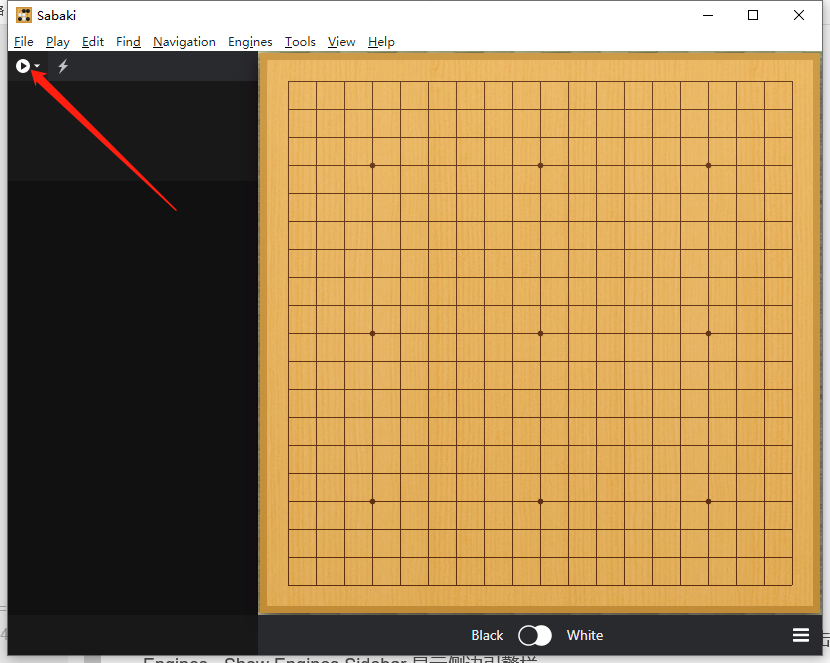
引擎栏点击 Attach Engine... 按钮，选择 Manage Engines...。

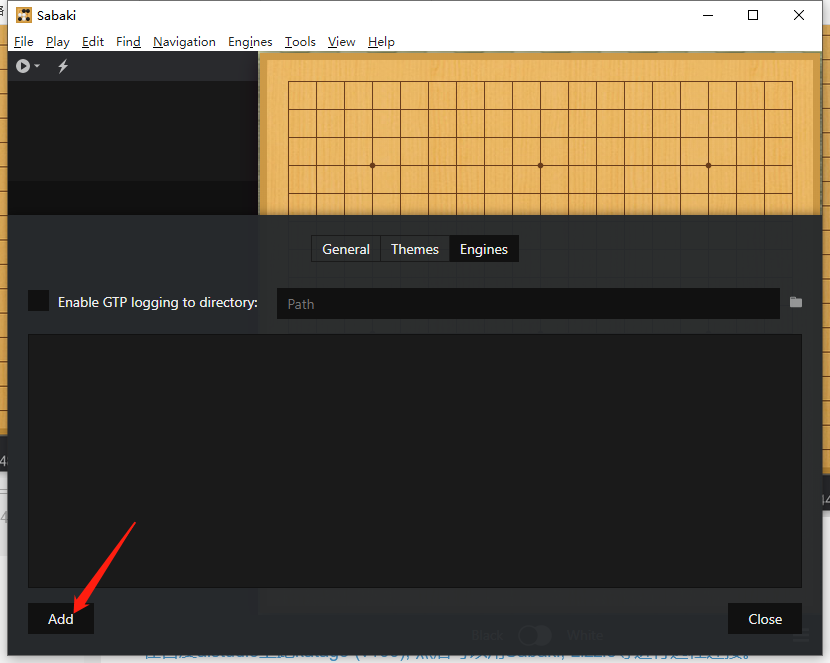
在引擎菜单中分别填写 4 行引擎信息。

引擎名称：自定义填写。

这里我写的是

matpool

路径：ikatago 客户端路径，可点击前方文件夹图标通过浏览选择。

D:\ikatago-1.3.3-win64\ikatago.exe

参数：ikatago 客户端参数，用户密码替换为服务端启动时的用户名和密码参数。

--platform all --username USER_NAME --password USER_PASSWORD

此次我的是

--platform all --username matpool --password sNoeoLSVDVrZ

初始命令：可定义一些命令参数，如定义 10 秒下一次棋。

time_settings 0 10 1

填写完成后点击 Close。

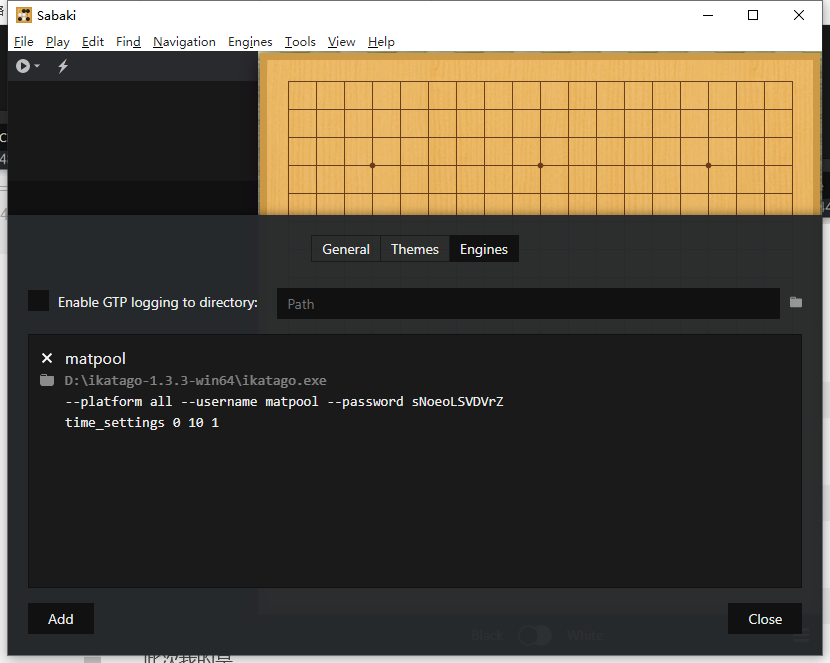
引擎栏点击 Attach Engine... 按钮，选择刚创建的引擎点击他。

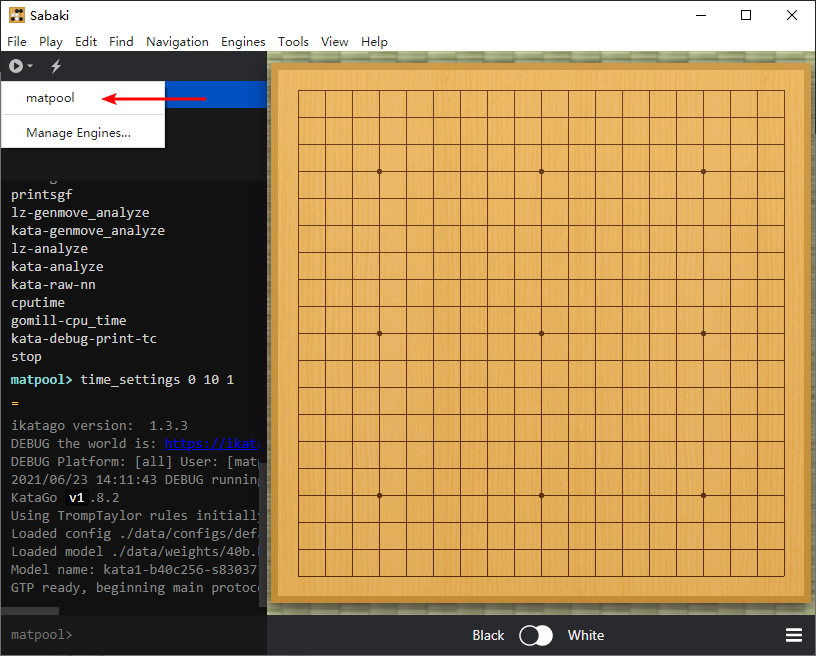
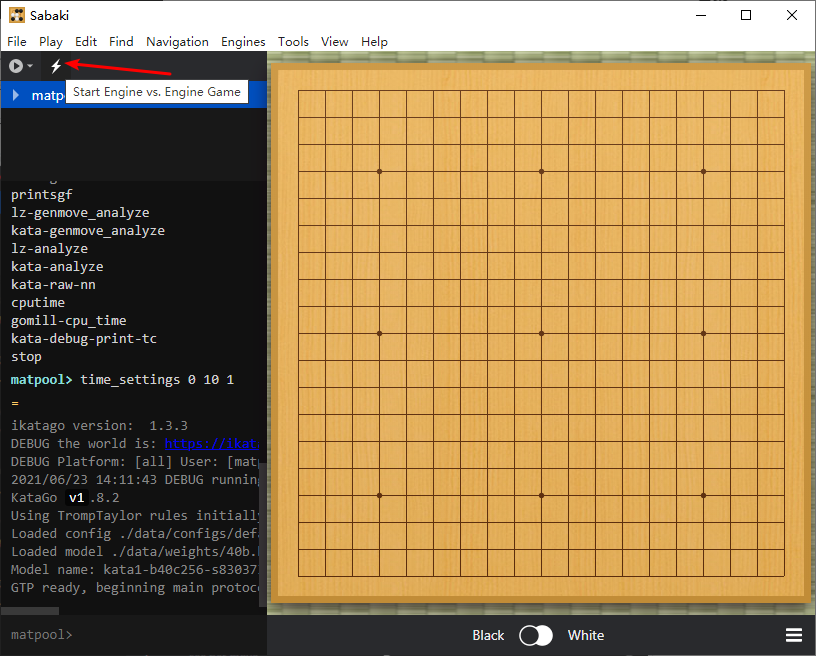
点击 Start Engine vs. Engine Game 开始机机对弈，每过 10 秒机器会走出一步。再次点击该按钮可以停止对弈。

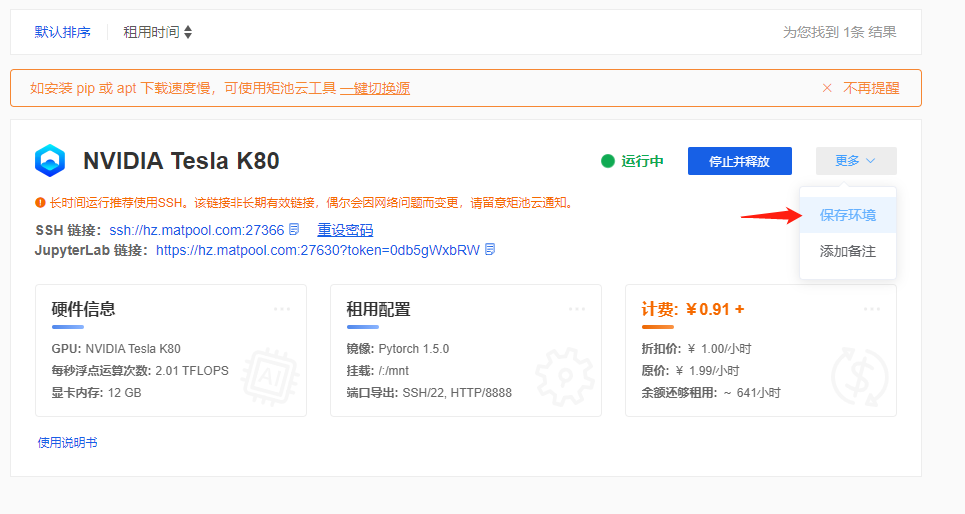
保存环境下次使用

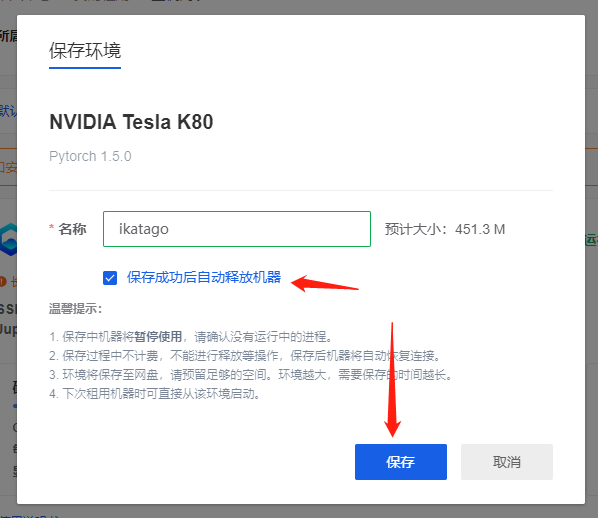
这样下次可以直接使用，不用再配置环境了。

详情可以查看如何使用矩池云的保存环境功能。

参考文章

在百度aistudio上跑katago (v100), 然后可以用Sabaki, Lizzie等进行远程连接。

ikatago-server