回溯剪枝，dfs，bfs

• dfs：

给定一个整数n，将数字1~n排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数n。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1≤n≤71≤n≤7

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

#############################################

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3
 4 const int N = 10;
 5 int n;
 6 int path[N];
 7 vector<bool> flag(N,false);
 8
 9 //dfs两个步骤：1：函数参数逐渐靠近叶子节点 2：处理好一个子过程
10 //dfs的参数就是递归树的层数，也就是path的路经，必须每一次递归都接近出口
11 void dfs(int u){
12     if(u == n){
13         for(int i = 0;i < n;++i)cout << path[i] << " ";
14         cout << endl;
15         return;
16     }
17     for(int i = 1;i <= n;++i){
18         if(flag[i] == false){
19             flag[i] = true;
20             path[u] = i;
21             dfs(u + 1);
22             flag[i] = false;
23         }
24     }
25 }
26
27 int main(){
28     cin >> n;
29     dfs(0);
30     return 0;
31 }

• 回溯剪枝：

n-皇后问题是指将 n 个皇后放在 n∗n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

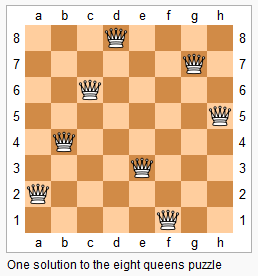
现在给定整数n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数n。

输出格式

每个解决方案占n行，每行输出一个长度为n的字符串，用来表示完整的棋盘状态。

其中”.”表示某一个位置的方格状态为空，”Q”表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

数据范围

1≤n≤91≤n≤9

输入样例：

4

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

###################################################

 1 #include <iostream>
 2 #include <vector>
 3 using namespace std;
 4
 5 const int N = 20;
 6 int n;
 7 char map[N][N];
 8 vector<bool> col(N,false),p(N,false),up(N,false);//col 用来判断当前列，p用来判断左斜对角线，up用来判断右斜对角线
 9
10 void dfs(int u){
11     if(u == n+1){
12         for(int i = 1;i <= n;++i){
13             for(int j = 1;j <= n;++j)
14                 cout << map[i][j];
15             cout << endl;
16         }
17         cout << endl;
18         return;
19     }
20
21     for(int i = 1;i <= n;++i){
22         if(!col[i] && !p[u+i] && !up[u + n - i]){
23             col[i] = p[u+i] = up[u+n-i] = true;
24             map[u][i] = 'Q';
25             dfs(u+1);
26             col[i] = p[u+i] = up[u+n-i] = false;
27             map[u][i] = '.';
28         }
29     }
30 }
31
32 int main(){
33     cin >> n;
34     for(int i = 1;i <= n;++i){
35         for(int j = 1;j <= n;++j)
36             map[i][j] = '.';
37     }
38     dfs(1);
39     return 0;
40 }

bfs：

走迷宫：

给定一个n*m的二维整数数组，用来表示一个迷宫，数组中只包含0或1，其中0表示可以走的路，1表示不可通过的墙壁。

最初，有一个人位于左上角(1, 1)处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角(n, m)处，至少需要移动多少次。

数据保证(1, 1)处和(n, m)处的数字为0，且一定至少存在一条通路。

输入格式

第一行包含两个整数n和m。

接下来n行，每行包含m个整数（0或1），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围

1≤n,m≤1001≤n,m≤100

输入样例：

5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例：

8
################################################

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3
 4 const int N = 110;
 5 int g[N][N];//地图
 6 vector<vector<int>> d(N,vector<int>(N,-1));//距离
 7 int n, m;
 8
 9 int bfs(int a, int b){
10     d[1][1] = 0;
11     queue<pair<int, int>> q;
12     q.push({a,b});
13     int dx[4] = {0,1,0,-1}, dy[4] = {-1,0,1,0};
14     //bfs模板就是队头出队，拓展
15     while(!q.empty()){
16         pair<int, int> t = q.front();
17         q.pop();
18         for(int i = 0;i < 4;++i){
19             int x = t.first + dx[i], y = t.second + dy[i];
20             if(x >= 1 && x <= n && y >= 1 && y <= m && d[x][y] == -1 && g[x][y] == 0)
21             {
22                 q.push({x,y});
23                 d[x][y] = d[t.first][t.second] + 1;
24             }
25         }
26     }
27     return d[n][m];
28 }
29
30
31 int main(){
32     cin >> n >> m;
33     for(int i = 1;i <= n;++i)
34         for(int j = 1;j <= m;++j)
35             cin >> g[i][j];
36     cout << bfs(1,1) << endl;
37     return 0;
38 }

bfs的一道比较难的题：

在一个3×3的网格中，1~8这8个数字和一个“X”恰好不重不漏地分布在这3×3的网格中。

例如：

1 2 3
X 4 6
7 5 8

在游戏过程中，可以把“X”与其上、下、左、右四个方向之一的数字交换（如果存在）。

我们的目的是通过交换，使得网格变为如下排列（称为正确排列）：

1 2 3
4 5 6
7 8 X

例如，示例中图形就可以通过让“X”先后与右、下、右三个方向的数字交换成功得到正确排列。

交换过程如下：

1 2 3   1 2 3   1 2 3   1 2 3
X 4 6   4 X 6   4 5 6   4 5 6
7 5 8   7 5 8   7 X 8   7 8 X

现在，给你一个初始网格，请你求出得到正确排列至少需要进行多少次交换。

输入格式

输入占一行，将3×3的初始网格描绘出来。

例如，如果初始网格如下所示：
1 2 3

x 4 6

7 5 8

则输入为：1 2 3 x 4 6 7 5 8

输出格式

输出占一行，包含一个整数，表示最少交换次数。

如果不存在解决方案，则输出”-1”。

输入样例：

2  3  4  1  5  x  7  6  8

输出样例

19

############################################

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3
 4 vector<string> g;
 5
 6 int bfs(string state){
 7     queue<string> q;
 8     unordered_map<string, int> d;//变换到每一个状态所需要的步骤
 9
10     q.push(state);
11     d[state] = 0;
12
13     int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
14     string end = "12345678x";
15
16     while(!q.empty()){
17         string t = q.front();
18         q.pop();
19         if(t == end)return d[t];
20         //状态转移
21         int tmp = d[t];//保存初始的状态的步骤
22         int k = t.find('x');
23         int x = k / 3, y = k % 3;
24         for(int i = 0;i < 4;++i){
25             int a = x + dx[i], b = y + dy[i];
26             if(a >= 0 && a < 3 && b >= 0 && b < 3){
27                 swap(t[k], t[a*3+b]);//找到对应一维数组的下标，然后交换
28                 if(!d.count(t)){//没有过这个状态
29                     d[t] = tmp + 1;
30                     q.push(t);
31                 }
32                 swap(t[k], t[a*3+b]);//在交换回来，因为还要从初始状态再转移到其他可行状态
33             }
34         }
35     }
36     return -1;
37 }
38
39 int main(){
40     char t[2];
41     string state;
42     for(int i = 1;i <= 9;++i){
43         cin >> t;
44         state += *t;
45     }
46     cout << bfs(state) << endl;
47     return 0;
48 }

 

end